websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesAerodynamics: Flow around the Ahmed Body

    Aerodynamics: Flow around the Ahmed Body

    This validation case belongs to fluid mechanics, representing the aerodynamics of the Ahmed body study. The aim of this test case is to validate the following parameters:

    • Drag coefficient computation
    • Velocity profiles

    The simulation results of SimScale were compared to the experimental data presented in [Ahmed]\(^1\).

    View Project

    Geometry

    The geometry is created based on the simplified aerodynamic body used by Ahmed et al\(^1\). See Figure 1 for dimensions and Figure 2 for the geometry. The slant angle (\(\phi\)) is set to 25°. The body is placed in a wind tunnel 6 \(m\) x 5 \(m\) x 13.5 \(m\) in order to limit the aerodynamic blockage effect.

    ahmed body geometry dimensions
    Figure 1: Dimensions of the Ahmed Body
    ahmed body geometry
    Figure 2: Three-dimensional view of the geometry used in the study

    Analysis Type and Mesh

    Tool Type: OpenFOAM®

    Analysis Type: Turbulent Incompressible fluid flow

    Mesh and Element Types:

    Mesh Mesh TypeNumber of Cells
    Mesh 1Standard3,746,887
    Mesh 2Standard6,915,859
    Mesh 3Standard10119321
    Table 1: Mesh details

    The Standard Mesher algorithm with tetrahedral and hexahedral cells was used to generate the mesh, with refinements near the walls and in the wake region (see Figure 3).

    ahmed body simulation mesh
    Figure 3: Mesh #3 of the three meshes investigated in the Ahmed body validation case

    A typical property of the generated mesh is the \(y^+\) (“y-plus“) value, which is defined as the non-dimensionalized distance to the wall, learn more. A \(y^+\) value of 1 would correspond to the upper limit of the laminar sub-layer.

    Wall treatment

    • Full Resolution in the near-wall region: The first cell lies at most at the boundary of the laminar sub-layer and no further. Here, \(y^+\) value is 1 or below.
    • Use of wall-functions to resolve the near-wall region: There is no need to place cells very close to the laminar sub-layer, and typically \(30 \le y^+ \le 300\).

    An average \(y^+\) value of 1 was used for the inflation layer around the body, and 150 for the floor. The \(k-\omega\) SST turbulence model was chosen, with full resolution for near-wall treatment of the flow around the body and with wall function for the floor.

    Simulation Setup

    Material

    Fluid

    Air with a kinematic viscosity of 1.5 x 10-5 \(kg/ms\) is assigned as the domain fluid.

    Boundary Conditions

    The boundary conditions for the simulation are shown in Figure 4 below:

    ahmed body boundary conditions
    Figure 4: Boundary conditions applied to the faces of the Ahmed body fluid domain
    Boundary Condition FaceValue
    Velocity inlet \([m/s]\)
    Turb. kinetic energy \([m^2/s^2]\)
    Specific dissipation rate \([1/s]\)    		Inlet60
    0.135
    180.1
    Pressure outlet \([Pa]\)Outlet0 (Fixed gauge pressure)
    Slip wallSide and top faces–
    No slip wall – Wall functionBottom face (Ground)–
    No slip wall – Full resolutionCar body–
    Table 2: Boundary Conditions for the Ahmed Body simulation

    The free stream velocity of the simulation is 60 \(m/s\), so that the Reynolds number based on the length of the body \(L\) is 4.29e6. Those are the same values presented in the original experiment of Ahmed and Ramm\(^1\).

    Reference Solution

    The experimental solution is presented in Figure 4 in the reference paper\(^1\) giving the value for the drag force coefficient for the slant angle \(\phi\) = 25°:

    $$ C_{d} = 0.2875 $$

    Result Comparison

    Drag Coefficient

    The drag force is defined as

    $$ F_{d}={\frac {1}{2}}\rho \,U^{2}\,C_{d}\,A_x $$

    where \(A_x\) (0.115 \(m^2\)) is the projected area of the Ahmed body in the streamwise direction and \(F_{d}\) the drag force. The drag force and drag coefficient were determined by the integration of surface pressure and shear stress over the entire Ahmed body (except for the 4 stilts acting as support).

    Mesh #2 was selected due to its accuracy and favorable results in relation to the simulation time. The resulting drag coefficient of the Ahmed body, closest to the reference solution as yielded by Mesh #2, was computed to be 0.2915, which is within a 1.217 % error margin of the measured value.

    Table 2 shows the result of the mesh independence study:

    Mesh
    		DRAG
    FORCE \([N]\)    		DRAG
    COEFFICIENT    		REFERENCEERROR [%]
    Mesh #173.7760.29850.28753.65
    Mesh #272.0430.29150.28751.217
    Mesh #370.1860.28350.2875-1.39
    Table 2: Results comparison and computed errors

    The difference in the error percentage magnitude between Mesh #2 and Mesh #3 is 0.173, indicating that the drag coefficient values are acceptable.

    Wake Flow Patterns

    The velocity streamline contour of the mean flow obtained with the simulation is reported in Figure 5, together with experimental results of reference.

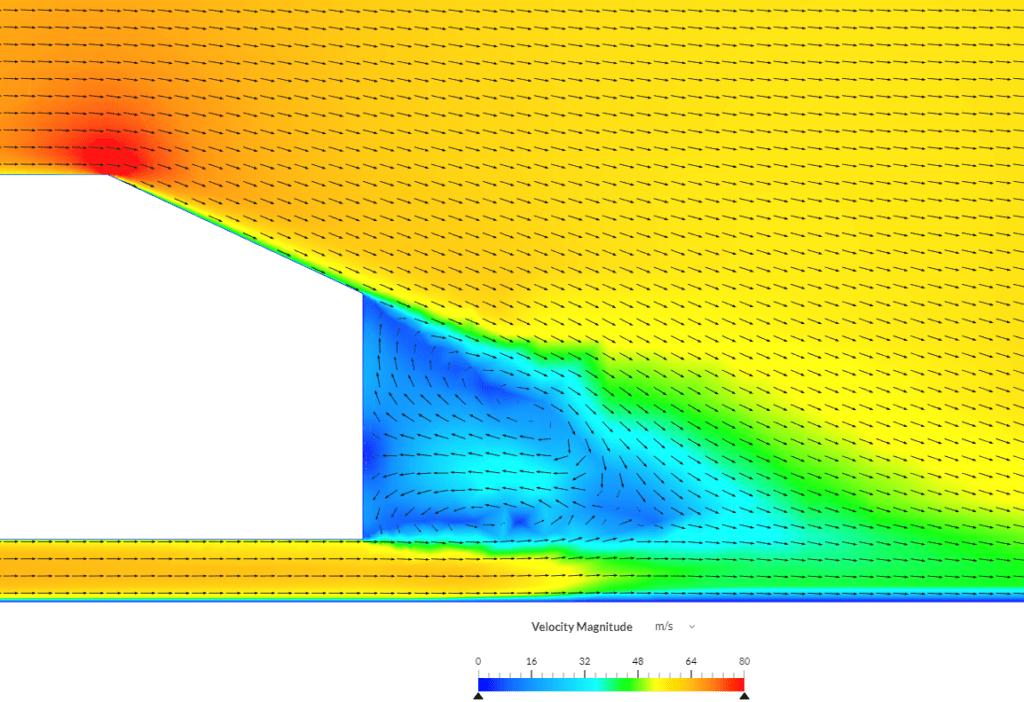
    ahmed body wake velocity vectors
    Figure 5: Velocity vectors and contours plotted with SimScale’s online post-processor
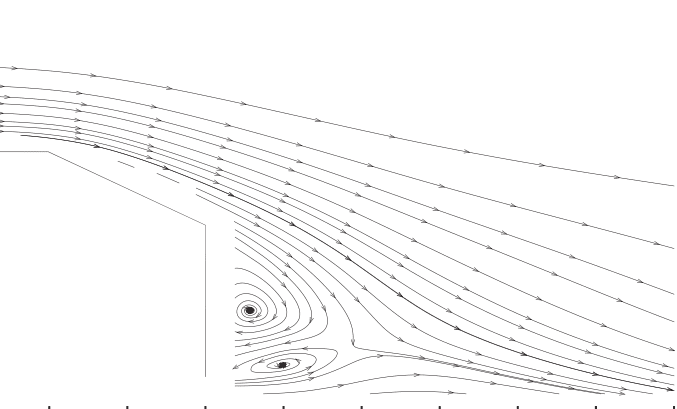
    ahmed body wake experimental results
    Figure 6: Experimental results for comparison showing a schematic of the streamlines over the Ahmed body

    References

    Note

    If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.

    Last updated: August 29th, 2025

    Contents