websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationSimulation SetupNumericsCFD Numerics: Non-Orthogonal Correctors

    CFD Numerics: Non-Orthogonal Correctors

    The non-orthogonality of a mesh is defined as the angle made by the vector joining two adjacent cell centers across their common face and the face normal.

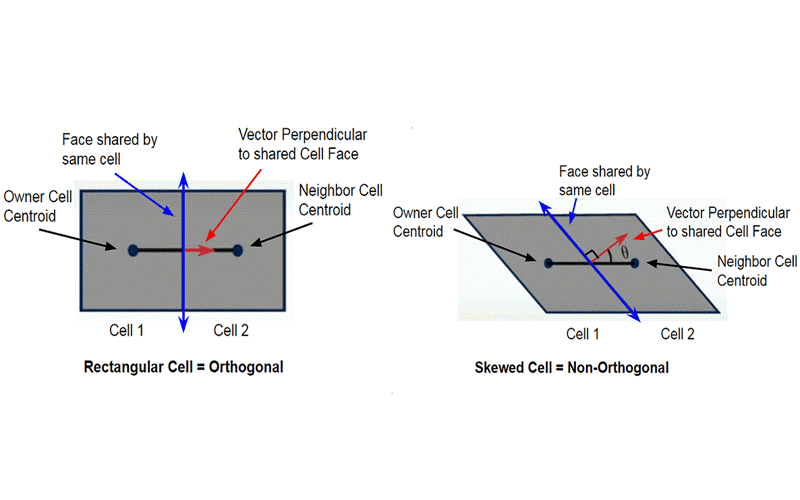
    orthogonality between two neighbor cells
    Figure 1: A vector perpendicular to the face shared by both cells creates an angle θ in relation to the vector connecting the cell centroids of cell 1 and neighbor cell 2. This is the Non-Orthogonality angle.\(^1\)

    As in real-life problems due to complex models, the numerical mesh is rarely orthogonal. So the non-orthogonality correction must be made for stability and accuracy. On the Scheme level, this is done under Numerics, where the Surface Normal Gradients and laplacian terms are corrected.

    For Meshes with non-orthogonality less than < 65-70, like the skewed cell in Figure 1, where the angle, θ, is sufficiently steep, the SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) solution algorithm is adequate for calculating the fluxes correctly. However, for bad quality meshes, an additional correction to account for mesh non-orthogonality is available in both SIMPLE and PISO algorithms in the standard OpenFOAM solver applications.

    When the mesh is bad (non-orthogonality > 75-80), the pressure calculation can be corrected by running several additional iterations of the pressure equation (inner loop). This is schematically represented below:

    non orthogonal corrector
    Figure 2: These corrections are the “Non-Orthogonal corrector” loops defined.

    So for a good mesh, with no need for non-orthogonal correctors, the default SIMPLE algorithm is performed, that includes the following steps:

    1. Momentum Equation;
    2. Pressure Equation;
    3. Check continuity;
    4. Energy Equation;
    5. Turbulence Equations etc.

    In case of a bad mesh, with two non-orthogonal correctors, two extra steps are added when solving the pressure equation during the SIMPLE algorithm, and the sequence is formed as follows:

    1. Momentum Equation
    2. Pressure Equation;
      • Pressure Equation ( correction 1)
      • Pressure Equation ( correction 2)
    3. Check continuity;
    4. Energy Equation;
    5. Turbulence Equations etc.

    The amount of non-orthogonal correctors that are selected should be corresponding to the mesh for the case being solved. Here are some recommended values for the non-orthogonal correctors based on mesh non-orthogonality:

    • if non-orthogonality < 70  : 0;
    • if non-orthogonality > 70  :  1;
    • if non-orthogonality > 80  :  2;
    • if orthogonality > 85, becomes challenging to converge.
    the non orthogonal correctors are specified according top the quality of the mesh prior to the simulation
    Figure 3: The number of non-orthogonal correctors is specified as part of the Numerics setup

    References

    Last updated: January 21st, 2022

    Contents