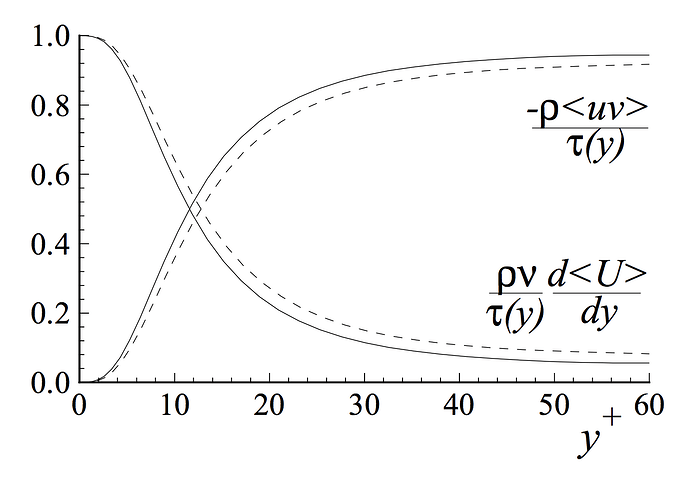What is y+ (yplus)?

Using SimScale Fluid Flow / CFD
1

There can never be a last word in regard to the axioms of any physical theory. All we can ask of them is that they lead to conclusions in agreement with observation. Sooner or later more refined observations will find the weak point in any set of physical axioms. Nature is far too complicated to be completely described in a few equations. - J.L. Synge (1938)

\underline{\textbf{Introduction}}

Before World War II, Johann Nikuradse (known from the Nikuradse Diagram) took a bunch of velocity measurements in smooth pipes at different distances from the inside wall surface and, in 1933, published his results with the title “Strömungsgesetze in rauhen Rohren” (“Laws of flow in rough pipes”). The first empirical friction law has already been proposed by ChĂ©zy in 1775 ^1, when this engineer had to determine the cross section of channels necessary to provide water to the city of Paris. In the 1860s, another French engineer called Bazin had taken measurements of velocity in rectangular and trapezoidal flumes, resulting in a huge amount of data sets. A big problem here was the trend lines didn’t match, although each set showed a relationship between velocity and wall distance. Nobody could write an equation to describe exactly how velocity behaves from the near wall region or far away from the wall until Nikuradse and his teacher, Prandtl, normalized the axes into y^+ (the axis that used to be the distance) and u^+ (the axis that used to be velocity). The result was that all the data sets perfectly matched. In addition, the two engineers could also write an equation that would fit u+ and y+ near the wall!

Prandtl_portrait
Prandtl_portrait1280×1802 370 KB

Figure 1: German engineer Ludwig Prandtl

In CFD (Computational Fluid Dynamics), that equation is still used as a function to figure out the shear stress at a wall node. In this SimWiki post, we are going to cover the fundamentals of y^+ as well as u^+, why they are used and why these values are very important!

\underline{\textbf{Why using wall functions?}}

Turbulent flows are an omnipresent phenomenon in CFD (Computational Fluid Dynamics) and are significantly affected by the presence of walls, where the viscosity-affected regions have large gradients in the solution variables. An accurate representation of the near wall region determines a successful prediction of wall bounded turbulent flows.

Some mature turbulence models such as k-\epsilon are only valid in the area of turbulence fully developed, and do not perform well in the area close to the wall. In order to deal with the near wall region, two ways are usually proposed.

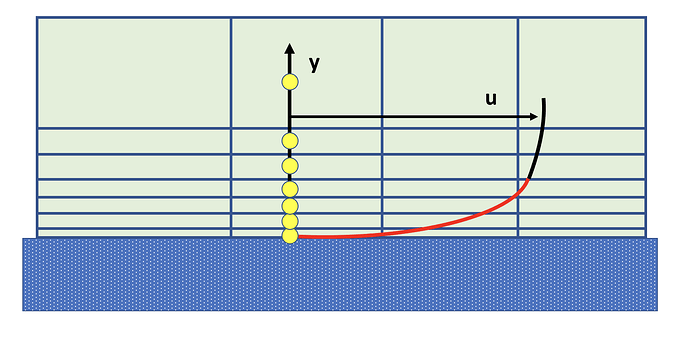
  1. One way is to integrate the turbulence to the wall. Turbulence models are modified to enable the viscosity-affected region to be resolved with all the mesh down to the wall, including the viscous sublayer. When using a modified low Reynolds turbulence model to solve the near-wall region, the first cell center must be placed in the viscous sublayer (preferably y^+ = 1) leading to the requirement of abundant mesh cells. Thus, substantial computational resources are required.

    • Use low-Re model like k-\omega
    • Good when you are interested in the forces on the wall (aerodynamics analyses for F1 cars, blade optimization in turbomachinery, etc.) ^3

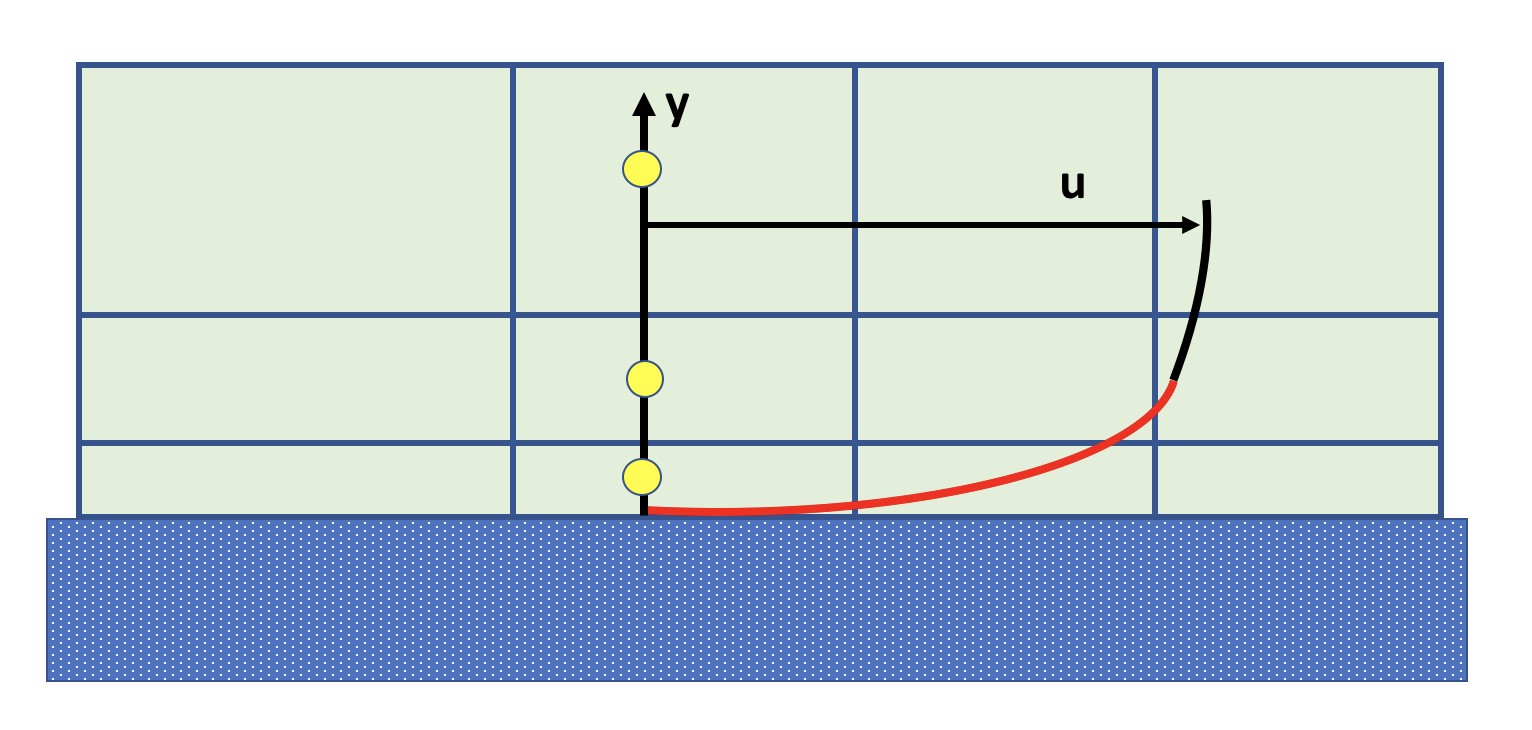
  1. Another way is to use the so-called wall functions, which can model the near wall region. Wall functions are equations empirically derived and used to satisfy the physics in the near wall region. The first cell center needs to be placed in the log-law region to ensure the accuracy of the results. Wall functions are used to bridge the inner region between the wall and the turbulence fully developed region. When using the wall functions approach, there is no need to resolve the boundary layer causing a significant reduction of the mesh size and the computational domain!

    • First grid cell needs to be 30 < y^+ < 300 (If this is too low, the model is invalid. If this is too high, the wall is not properly resolved.
    • Use high-Re model (Standard k-\epsilon, RNG k-\epsilon)
    • Use when you are more interested in the mixing rather than the forces on the wall ^3

Viscous%20Sublayer%20Resolving%20Approach%20SimScale
Viscous%20Sublayer%20Resolving%20Approach%20SimScale1544×758 23.8 KB

Figure 2: Viscous sublayer resolving approach to resolve boundary layer (in red)

Log-Based%20Wall%20Functions%20SimScale
Log-Based%20Wall%20Functions%20SimScale1532×730 19.4 KB

Figure 3: Logarithmic-based Wall functions to resolve boundary layer (in red)

\underline{\textbf{Wall functions}}

“At a high Reynolds number, the viscous sublayer of a boundary layer is so thin that it is difficult to use enough grid points to resolve it” (Ferziger and Perić 2002).

The wall functions rely on the universal law of the wall, which basically states that the velocity distribution very near to a wall is similar for almost all turbulent flows. One of the most prominent parameters when judging the applicability of wall functions is the so-called dimensionless wall distance y^+ (Schlichting and Gersten 2001) denoted by:

y^+ = \frac{y u_\tau}{\nu} \tag{1}
  1. u_\tau is the so called friction velocity
  2. y is the absolute distance from the wall
  3. \nu is the kinematic viscosity

One can interpret y^+ as a local Reynolds number, which means that its magnitude can be expected to determine the relative importance of viscous and turbulent processes. Figure 2 shows the fractional contributions to the total stress from the viscous and Reynolds stresses in the near wall region of channel flow. (Pope)

PopeContributionsViscousAndReynoldsStresses
PopeContributionsViscousAndReynoldsStresses1200×844 64.4 KB

Figure 4: Profiles of fractional contributions of the viscous and Reynolds stresses to the total stress. DNS data of Kim et al. (1987): dashed lines, Re = 5,600; solid lines, Re = 13,750.

One can easily see that if we are in the viscous wall region with y^+ < 50, there is a direct effect of the viscosity on the shear stress. Conversely in the outer layer with y^+ > 50, the effect of viscosity is neglibile.

For the sake of completeness, let’s briefly introduce the friction velocity u_\tau. It should be evident that the viscosity \nu and wall shear stress \tau_w are important parameters. From these quantities and \rho we define the viscous scales being appropriate viscous scales and lengthscales in the near-wall region.

u_\tau = \sqrt{\frac{\tau_w}{\rho}} \tag{2}

with

\tau_w = \rho \nu \left(\frac{d<U>}{dy} \right)_{y = 0} \tag{3}

The dimensionless velocity is given by:

u^+= \frac{u}{u_\tau} \tag{4}

Stephen B. Pope (2000) comments on the steep velocity profile near the wall and how turbulence model needs to take this into account. This is also the point where wall functions come into play, first suggested by B.E. Launder and Spalding (1972). The basic idea is that additional boundary conditions are applied at some distance to the wall to fulfill the log-law. Hence the additional equations introduced by the turbulence model are not solved close to the wall. Depending on the turbulence model used, different wall functions must be applied to respective fields of the turbulence model, which means that k-\epsilon has different wall functions than the k-\omega model.

Due to this fact, the different turbulence models and the associated wall functions require different values of y^+ as well as different spatial resolutions of the near wall area. Please note that if the log-law region is resolved geometrically by the mesh, no wall functions must be applied! The downside of this approach is that depending on the simulation, such low y^+ values are hard to create during the pre-processing step (meshing) or even undesirable, as this will significantly decrease the time step!

In SimScale (using OpenFOAM as its CFD solver), wall functions are nothing else than boundary conditions that are applied to boundary patches of type wall, rather then a usual patch.

\underline{\textbf{Wall Regions and Layers as well as their Properties}}

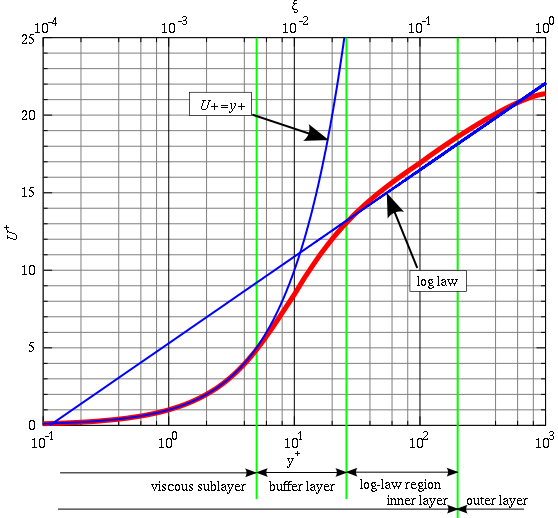
  1. The viscous sublayer (y^+ < 5)
    In the viscous layer, the fluid is dominated by the viscous effect, so it can be assumed that the Reynolds shear stress is negligible. The “linear velocity law” is given by:
u^+ = y^+ \tag{5}
  1. The logarithmic area (y^+ > 30)
    In the logarithmic layer, turbulence stress dominate the flow and velocity profile varies very
    slowly with a logarithmic function along the distance y. Formula (6) describes this region with the Karman constant \kappa of 0.41 and the constant B = 5.2.
u^+ = \frac{1}{\kappa} ln(y^+) + B \tag{6}
  1. The Buffer layer (5 < y^+ < 30)
    The buffer layer is the transition region between the viscosity-dominated region and turbulence-dominated part of the flow. Viscous and turbulent stresses are of similar magnitude and since it is complex, the velocity profile is not well defined and the original wall functions avoid the first cell center located in this region.

svg
svg558×518 32.4 KB

Figure 5: The Law of the Wall

\underline{\textbf{Best Practices}}^2

  • In the pre-processing stage of the simulation we need to make sure that y^+ is in the desired range. For that, we have to calculate the size of the first layer of our mesh.

  • Check the y^+ value after the computation again as the real flow field will develop during the simulation and a remesh might be necessary.

    • To avoid a remesh (and the use of too many core hours), it makes sense to really calculate the value beforehand.

\underline{\textbf{Step-by-Step: Calculating Wall distance with a given y+}}

  1. Write down definition of y^+ and rearrange for y
y^+ = \frac{y u_\tau}{\nu} \space \rightarrow \space y = \frac{y^+ \nu}{u_\tau} \tag{7}
  1. Next, we calculate u_\tau
u_\tau = \sqrt{\frac{\tau_w}{\rho}} \tag{8}
  1. The wall shear stress \tau_w can be calculated from the skin friction coefficient C_f
\tau_w = \frac{1}{2} C_f \rho U^2_\infty \tag{9}
  1. Determine the skin friction coefficient (for example, for a flat plate with the 1/7 power law)
C_f = 0.0576 Re_d^{-\frac{1}{5}} \tag{10}

  1. The Reynolds number is known. Insert that into formula (10), the result in formula (9) and this into (8)

  2. Now insert everything into formula (7) with your wanted y^+ and you are finished!

Alternatively use a y^+ calculator: CFD Online - Y-Plus Wall Distance Estimation

A list of skin friction coefficients can be found here: Skin friction coefficient -- CFD-Wiki, the free CFD reference

\underline{\textbf{Limitations of Wall Functions}}^2

Limitations%20of%20Wall%20Functions%20-%20SimScale
Limitations%20of%20Wall%20Functions%20-%20SimScale817×215 63.4 KB

Figure 6: Wall functions and their limits

In the case of a boundary layer separation as depicted above, one should not use wall functions because the log-based wall functions do not correctly predict the profile. One should directly resolve the viscous sublayer to obtain accurate results.

\underline{\textbf{Other options for Wall Modelling}}^3

  • Enhanced Wall Treatment Option

    • Combines a blended law-of-the wall and a two-layer zonal model
    • Suitable for low-Re flows or flows with complex near-wall phenomena
    • Generally requires a fine near-wall mesh capable of resolving the viscous sublayer (y^+ < 5, and a minimum of 10–15 cells across the “inner layer" (viscous sublayer, buffer and log-law layers))

  • Scalable Wall Functions

    • In practice, many users often fail to maintain 30 < y^+ < 300
    • Iteration by iteration, the first cell may change from being either inside or outside of the viscous sublayer, which can lead to instabilities.

\underline{\textbf{Project Example}}

TurbulentPipeFlow-mesh
TurbulentPipeFlow-mesh896×877 16 KB
TurbulentPipeFlow-mesh2
TurbulentPipeFlow-mesh2600×610 8.21 KB

Figure 7: Meshes used for the Turbulent Pipe Flow validation: left is used for wall function (y^+ ≈ 30) approach, right for full resolution (y^+ ≈ 1) approach.

This validation case can be found here: Turbulent Pipe Flow Validation

\underline{\textbf{Y+ (yplus) - Generate Wall Spacing for CFD on SimScale}}

The following page explains how you can generate the desired y+ (yplus) value on SimScale and check if your settings are correct: Y+ (yplus) - Generate Wall Spacing for CFD

\underline{\textbf{Literature}}:

  • F. Liu - A Thorough Description Of How Wall Functions Are Implemented In OpenFOAM

  • S. M. Salim, S.C. Cheah - Wall y^+ Strategy for Dealing with Wall-bounded Turbulent Flows

  • T. Marić, J. Höpken, K. Mooney - The OpenFOAM Technology Primer

  • Stephen B. Pope - Turbulent Flows

\underline{\textbf{References}}:

[1] - A. Chezy - Formule pour trouver la vitesse de l’eau conduite dans une rigole donnĂ©e

[2] - Turbulence Fluent Notes

[3] - Fluid Lecture 06 Turbulence

\underline{\textbf{Pictures}}:

\underline{\textbf{Acknowledgement}}:

I am deeply grateful to Barry (@Get_Barried), Darren (@1318980), as well as Jozsef Nagy for proofreading and making suggestions to make sure users can get most out of this SimWiki article.

18 Likes
2

Brilliant work @jousefm! Looking forward to more!

2 Likes