CFD Numerics: Relaxation Factors

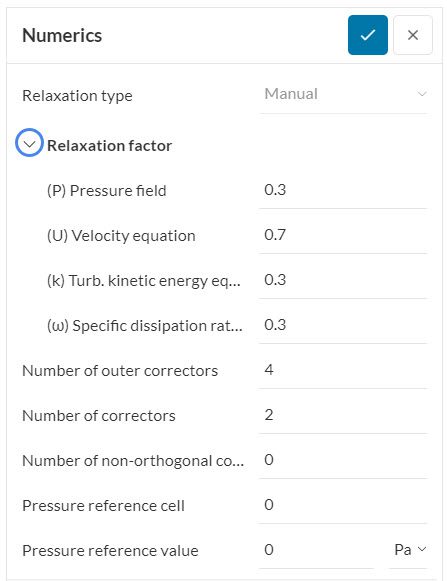
Relaxation factors control the under-relaxation of the solution. This is a technique used for improving the stability of a calculation, especially in solving steady-state analysis, where the first iterations are critical.

Numerics panel relaxation factors for incompressible turbulent case — Figure 1: The *Relaxation factor* settings are located in the *Numerics* panel, and have different default values depending on the properties of the simulation.

Manual Relaxation

The best choice of the relaxation factor is one that is small enough to ensure stability but large enough to move the iterative process to convergence at a decent speed. For example, if $α$ is the relaxation factor then a value of $α$ that is:

< 0.15 is not advisable as it will slow down the solution too much.
> 0.7 can cause unstable solution.
> 0.9 is not recommended as it can cause divergence.

In the case of manual relaxation, values between 0.3 < $α$ < 0.7 are recommended.

Auto-Relaxation

The auto-relaxation feature is designed to dynamically change the factor $α$ for the flow variables to speed up convergence while trying to keep the solution stable. In some cases, if this causes divergence, it is recommended to try with manual relaxation factors that are fixed over the iterations.

Under-Relaxation

The method of under-relaxation is basically limiting the amount by which a variable changes from the previous iteration to the next one. Due to the nonlinearity in the equations, it is important to control the change of the variable.

Because of the non-linearities of the equations being solved, it is necessary to control the change of variable $φ$. This is achieved by under-relaxation as follows:

$$ {φ_P}^n = {φ_P}^{n-1} + α \times\ ({{φ_P}^{n*}\ – {φ_P}^{n-1}}) $$

Where $α$ is the factor that defines the relaxation such that:

$α$ < 1 means under-relaxation. This will slow down the convergence rate but increase the stability.
$α$ = 1 means no relaxation at all. The predicted value of $φ$ is simply used.
$α$ > 1 means over-relaxation. It can sometimes be used to accelerate the convergence rate but will decrease stability.

And:

$n$ refers to the new, used value of $φ_P$;
$n-1$ refers to the previous value of $φ_P$;
$n*$ refers to the new, predicted value of $φ_P$.

This means that the new value of the variable $φ$ depends upon the old value, the computed change of $φ$, and $α$.

The under-relaxation factor $α$, specifies the amount of under-relaxation, such that:

If $α$ decreases, the under-relaxation increases.
If $α$ < 1 means the solution is under-relaxed. The specified fraction of the predicted value change is used. This may slow convergence but increases stability.
If $α$ = 1 there is guaranteed matrix diagonal equality, and no under-relaxation. The predicted value is simply taken.
If $α$ = 0 the solution does not change with successive iterations.

Relaxation for Multi-Purpose Solver

When applying the Multi-purpose solver, there are two different categories of relaxation factors in the Numerics tab that can be altered. The first type, depicted below, concerns the update of the corresponding variable involved during the iterative process.

Setting for the relaxation factors concerning the variable update in the iterative process — Figure 2: Relaxation factor settings for the update of variables during the iterative process

For this category the value set for $α$ also ranges from 0<= $α$<=1, nonetheless it obeys the following rule:

$α$ = 0 corresponds to full application of corrected value (similar to $α$=1 for the cfd solver) at the end of the iteration step. It is recommended when no convergence problems are assumed.
$α$ = 1 corresponds to no application of corrected value (similar to $α$=0 for the cfd solver) at the end of the iteration step.
For 0< $α$<1, an increment of the corrected value is added to the corresponding variable (from the previous iteration) at the end of the current iteration step.

On the other hand, the second category, “Diagonal Relaxation Factors”, influences the convergence of solutions from linear systems of equations associated with a specific variable, as shown below.

Settings for the relaxation factors concerning the solution of the linear system of equations for differetn variables — Figure 3: Relaxation factor settings for the solution of a linear system of equations from different variables within the Multi-purpose solver

These factors aim to improve convergence and stability by modifying the diagonal terms of the coefficient matrix in the linear system of equations and obey the following rule:

$α$ may range from 0 to infinity, but typical values range from 0.001 to 1.
$α$> 0.3 are recommended for cases where difficult convergence is expected or has already been observed.
If $α$ = 0 is assigned, then the full corrected value is applied.

The higher the value assigned to the $α$, the more conservative is the correction procedure, requiring more iterations to reach desirable convergence

Last updated: September 2nd, 2025

Did this article solve your issue?

How can we do better?

We appreciate and value your feedback.