Documentation
This turbulent pipe flow validation case belongs to fluid dynamics. The aim of this test case is to validate the following parameters:
The simulation results of SimScale were compared to a reference solution based on the Power law velocity profile presented by Henryk Kudela in one of his lectures\(^1\).
The geometry can be seen below:
This is a cylindrical pipe with a diameter of 0.01 \(m\), and a length of 1 \(m\).
Tool Type: OpenFOAM®
Analysis Type: Incompressible steady-state analysis.
Turblence Model: Two turbulence models were tested, the k-epsilon and the k-omega SST.
Mesh and Element Types:
Two approaches were tested in this validation case: Wall functions and full resolution on the walls. For the wall functions, the desired \(y^+\) range is [30 , 300], and the generated mesh looks like this:
Full resolution on the walls requires a \(y^+\) lower than \(1\), so the final mesh has the following form:
More details about the meshes used in the three cases can be seen bellow:
| Cases | Near-wall approach | Number of cells | Mesh type | Turbulence model |
|---|---|---|---|---|
| A | Wall functions | 176574 | Standard | k-omega SST |
| B | Wall functions | 176574 | Standard | k-epsilon |
| C | Full resolution | 1393776 | Standard | k-omega SST |
Fluid:
Boundary Conditions:
Initial Conditions:
The velocity profile for turbulent pipe flow is approximated by the Power-law velocity profile equation \(^1\):
$$\bar{u}_y(r) = \bar{u}_{y_{max}}\left(\frac{R-r}{R}\right)^{1/n}$$
where:
For turbulent flow, the ratio of \(u_{y_{max}}\) to the mean flow velocity is a function of \(Re\). In this case, this ratio is calculated to be 1.224.
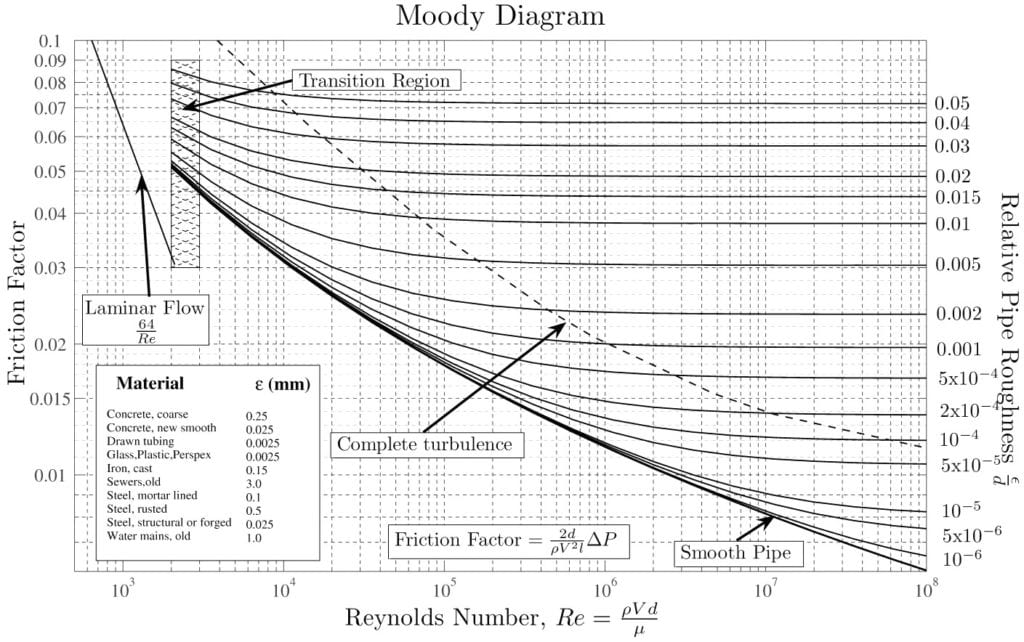
The pressure drop for turbulent flow in pipes is obtained by using the Darcy-Weisbach \(^2\):
$$\Delta P = f\ \frac{\rho\ u^2 \ l}{2 \ d}$$
where:
According to the Moody diagram (Figure 4) and for this case, the value of \(f\) is 0.0309.
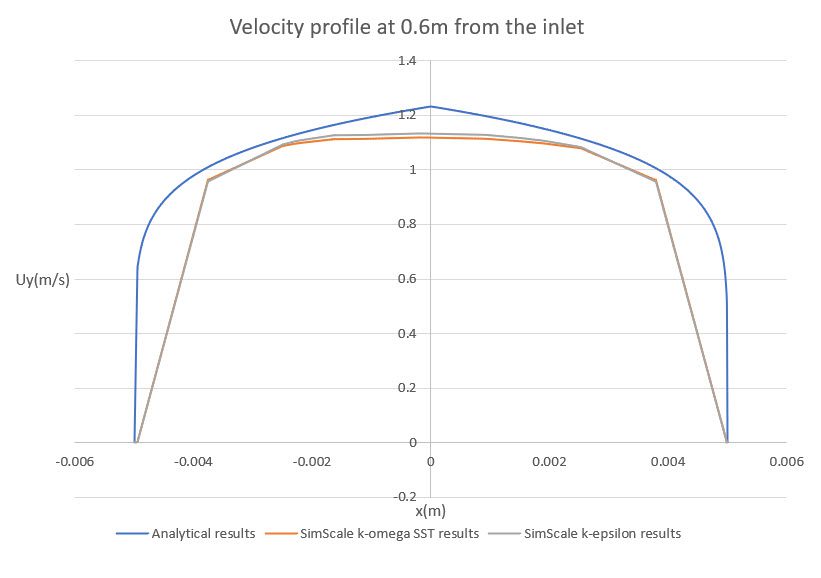
For the “wall function approach” the average \(y^+\) value on the walls of the pipe is 31.95 for k-omega SST and 32.39 for k-epsilon.
Pressure drop along the pipe length can be observed below:
The following graph shows the developed velocity profile, located 60 \(cm\) from the inlet:
For “full resolution”, the average value for \(y^+\) is 0.017. The corresponding graphs are created:
The pressure drop along the pipe length:
The developed radial velocity profile, located 60 \(cm\) from the inlet:
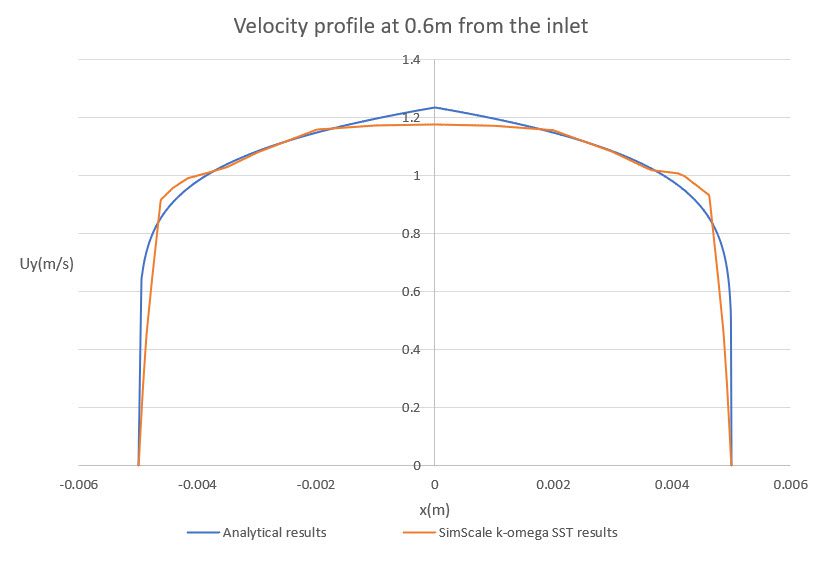
Besides good agreement with the Power law model, results show that all approaches and turbulence models are successful in predicting the pressure drop along pipe length for the given meshes.
Note
If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.
Last updated: July 5th, 2023
We appreciate and value your feedback.
Sign up for SimScale
and start simulating now