websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Quadcopter Ground to Air Thrust

    Validation Case: Quadcopter Ground to Air Thrust

    This validation case belongs to fluid dynamics. This test case aims to validate the following parameters for a quadcopter drone thrust in ground proximity:

    • Ratio of Thrust at ground to Thrust in free air.

    The simulation results of SimScale were compared to the research performed by C. Paz, E. Suarez and C. Gil, J. Vence published in the paper “Assessment of the methodology for the CFD simulation of the flight of a quadcopter UAV” in November 2021\(^1\).

    The analytical method used in the research paper is derived from measurements for a slightly different quadcopter, with blades of the same radius.

    View Project

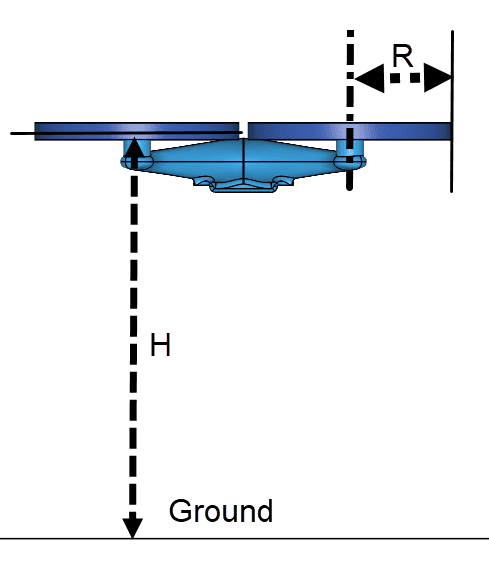
    To compare SimScale to the results in [1], an analysis of different distances from a quadcopter drone to the ground is performed and the thrust ratios are compared. Distance from ground and rotor radius dimensions are taken as shown in Figure 1:

    Validation Case: Thrust Ground Proximity for Quadcopter 00_Drone_Height_Radius_Ratio
    Figure 1: Height position of the drone and blade radius are used to calculate the height to radius ratio.

    Geometry of Quadcopter

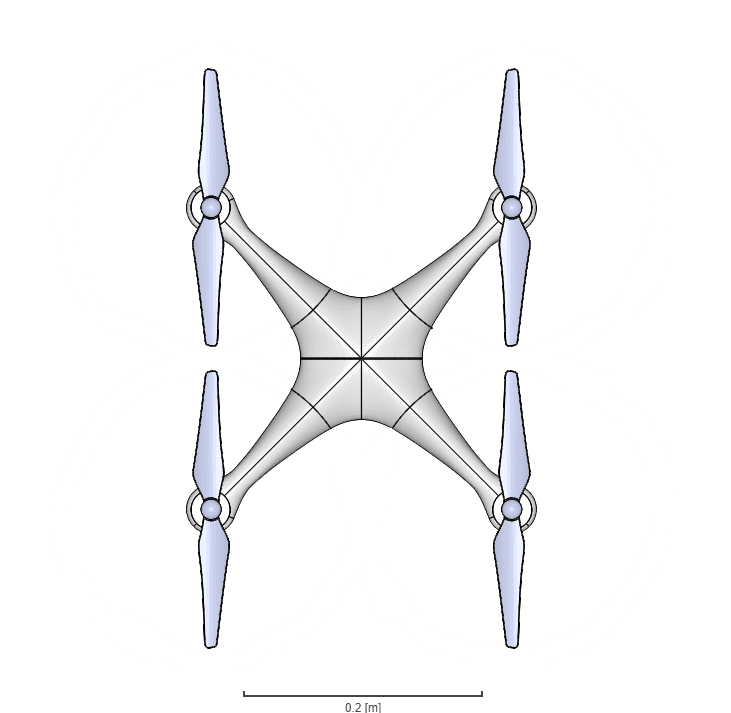
    The quadcopter geometry used for this case can be seen below:

    Validation Case: Thrust Ground Proximity for Quadcopter _ Geometry
    Figure 2: DJI-Phantom drone, without the landing legs and camera

    It’s a DJI-Phantom quadcopter with the landing leg and camera removed. the DJI-Phantom is a quadcopter drone used in multiple applications. The rotor blades of the drone were all aligned as seen in Figure 3:

    Validation Case: Thrust Ground Proximity for Quadcopter _ Blade Alignment
    Figure 3: Position of the drone blades, aligned with the drone body. Multiple blade positions were tested in the research by E. Suarez and J. Vince \(^1\)

    Analysis Type and Mesh

    Analysis Type: Steady-State, Multi-purpose analysis with MRF rotating zone, using the k-epsilon turbulence model.

    Mesh Sensitivity Analysis

    The Multi-purpose mesher algorithm with hexahedral cells was used to generate the mesh. Multiple meshes with incrementally increasing refinement were generated in parallel using the automatic meshing functionality before comparing different height setups.

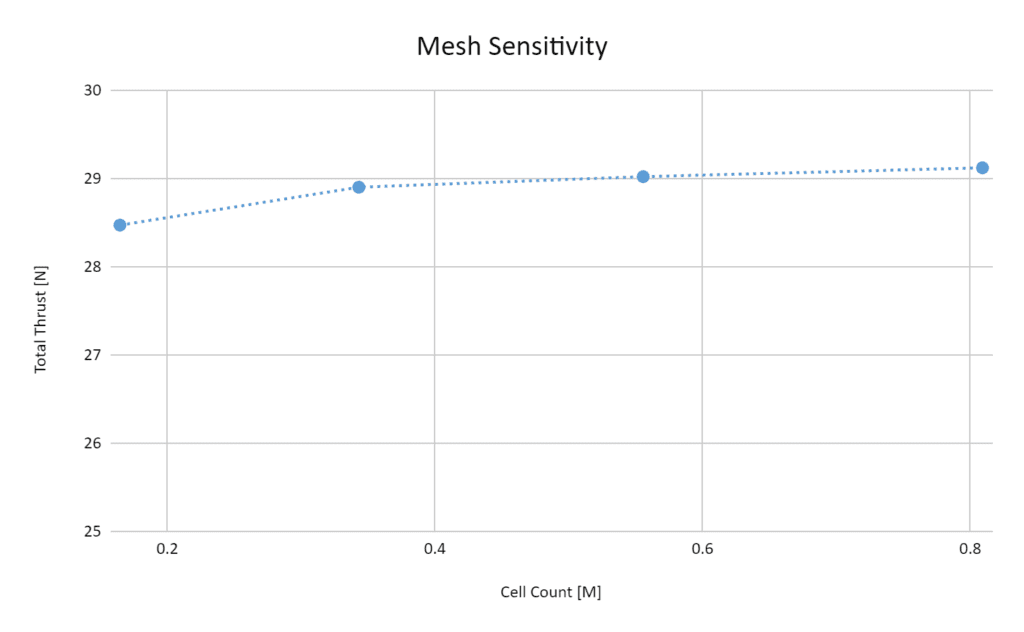
    Thrust Ground Proximity for Quadcopter _ mesh sensitivity
    Figure 4: Mesh sensitivity results show convergence of the total thrust for a cell count of more than 0.5 million.

    As seen in Figure 4 the total thrust converges to 29 \( N \) for a cell count higher than 0.5 million cells, with a deviation of less than 1 % between 0.55 and 0.8 million cells. Therefore all results with a cell count higher than 0.55 are considered mesh insensitive.

    Drone Propeller Study

    A validation case for single propeller has already been documented and can be accessed below where a further investigation into the mesh of a single propeller has been performed.

    Validation Case: Drone Propeller Study

    Simulation Setup

    Material:

    • Air
      • \((\nu)\) Kinematic viscosity: 1.529e5 \(m^2/s\)
      • \((\rho)\) Density: 1.196 \(kg/m^3\)

    Boundary Conditions:

    • Inlet & outlet:
      • Total gauge pressure \(P\) of 0 \(Pa\)
      • Turbulent kinetic energy \(k\) with an inlet value of 3.75 e−3 \(m^2 s^2\)
      • Specific dissipation rate \(\omega\) with an inlet value of 3.375 1 \(s\)
    • Slip walls on the rest of the domain faces to represent an open-air environment.

    Reference Solution

    Thrust Changes Due To Ground Proximity

    To compare the results gained by SimScale with the published results \(^1\) the Sanches-Cuevas Equation is used.

    $$ \frac{T_{IGE}}{T_{OGE}} = \frac{1}{1-(\frac{R}{4H})^2-R^2(\frac{H}{\sqrt{(d^2+4H^2)^3}})-(\frac{R^2}{2}) (\frac{H}{\sqrt{(2d^2+4H^2)^3}}) -2R^2 (\frac{H}{\sqrt{(b^2+4H^2)^3}})K_{b} } \tag{1} $$

    Where,

    • \( T_{IGE}\) = Thrust of the propellor in closed ground condition
    • \( T_{OGE}\) = Thrust of the propellor in free air condition
    • \(R\) = Radius of the rotor
    • \(H\) = vertical distance to the ground
    • \(d\) = distance between the adjacent rotor axis
    • \(b\) = diagonal distance of the rotor axis
    • \(K_{b}\) = Imperical body lift coefficient (Value for this study \( K_{b}=2\))

    Result Comparison

    Comparison of the \( \frac{T_{IGE}} {T_{OGE}} \) ratio obtained from the SimScale results against the results obtained from [1] is given below:

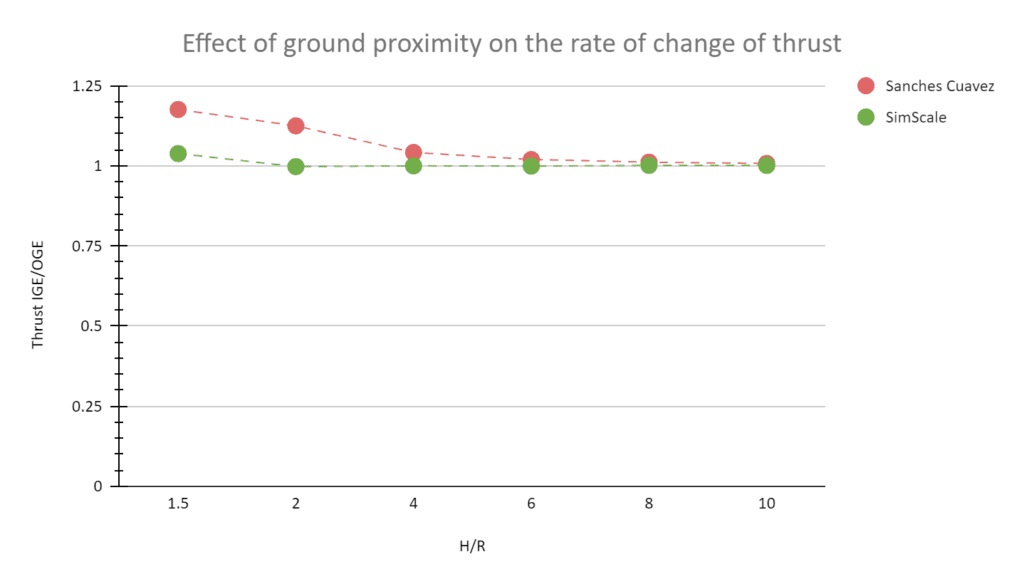
    Thrust Ground Proximity for Quadcopter _ comparison to Sanchez Cuevas curve
    Figure 5: Simulation results compared to the data from the formula show a good correlation with the SimScale results, especially for higher height to radius \((H/R)\) ratios.

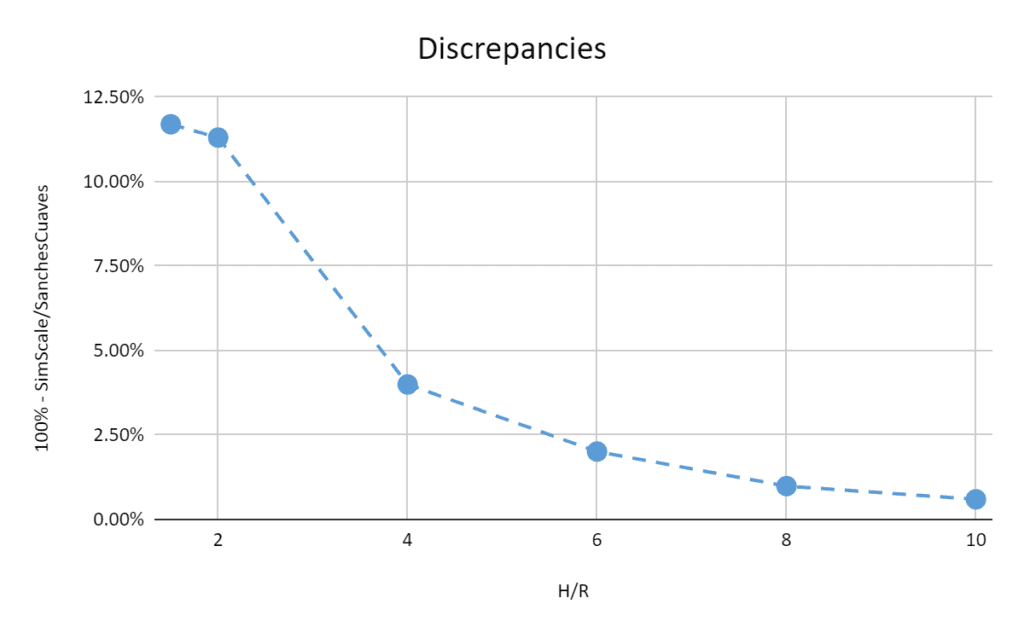
    The SimScale result for the quadcopter shows a good correlation with the Sanches Cuevaz curve, especially for height to radius ratios higher than four. The percentage of error is high for low \(H/R\) ratios because the SimScale data is compared with the analytical data, which does not account for close-to-ground effects, SimScale does.

    Below are the discrepancies for each run:

    validation- Thrust Ground Proximity for Quadcopter -discrepancy
    Figure 6: Discrepancy for different height to radius ratios. The decreasing discrepancy for higher ratios is noticeable.

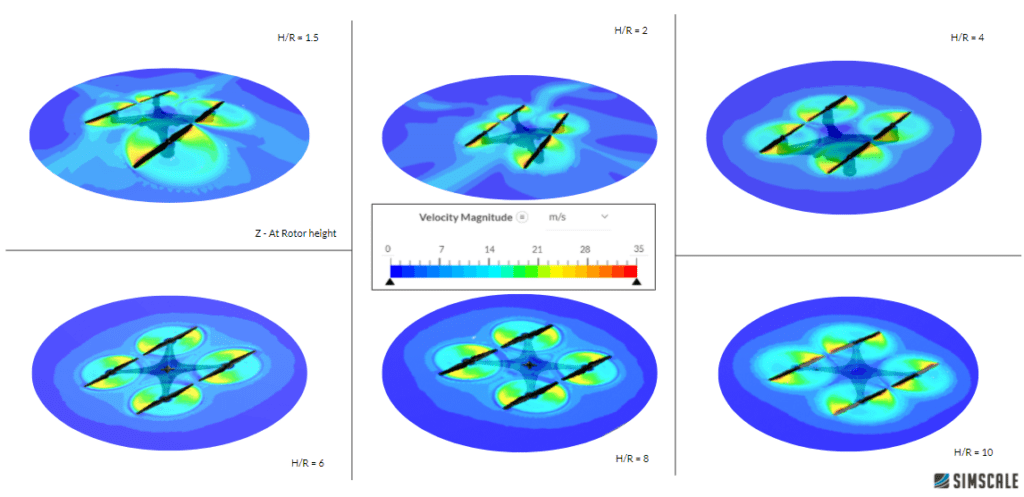
    In the following Figure 7, the velocity is plotted at the rotor plane for different heights. It is noticeable that for higher heights the influence of the ground is not noticeable.

    Validation Case: Thrust Ground Proximity for Quadcopter rotor_velocity
    Figure 7: Effect of the rotor velocity for different ground distances. The repulsing flow from the ground can be seen for low H to R ratios.

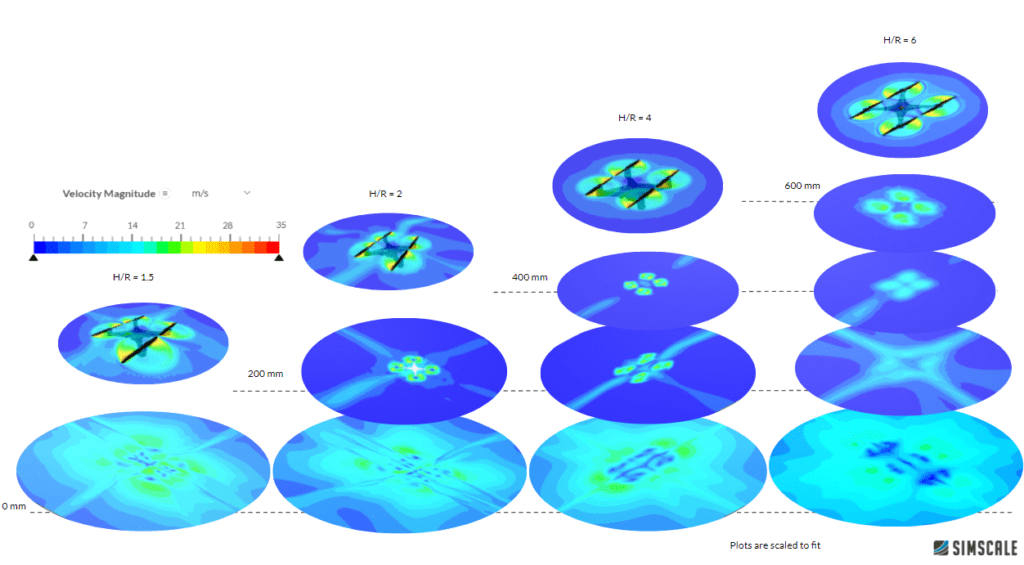
    The velocity at different heights can be seen in the figure below. As expected with the increasing distance of the quadcopter from the ground, the velocity at the ground is slower and more diffuse which decreases the thrust of the quadcopter.

    Validation Case: Thrust Ground Proximity on Quadcopter_ section velocyties
    Figure 8: Velocity for different height to radius ratios. The velocity is displayed for the same height in the different cases.

    References

    Note

    If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.

    Last updated: August 13th, 2024

    Contents