Field Calculations

Under Field calculations, the user can define a series of additional outputs for their simulations, including total pressure, vorticity, amongst others.

New field calculations can be defined under the Result control tab, as in Figure 1:

Below, we will go over each one of the Field calculation options available in SimScale.

Pressure Fields

The pressure field control is only available for the incompressible analysis type. With this field calculation, the user can define a series of different outputs, most notably Total pressure and Pressure coefficient, also known as \(C_p\). Find below some useful configurations.

Total Pressure

For incompressible analysis, the default pressure values shown in the post-processor are gauge static pressures. If you are interested in having one additional scalar showing total pressures, this is also possible. Find below one sample result control configuration:

The platform will perform the following equation to show total pressure in the post-processor:

$$P_{Total} = P_{Gauge,\ static} + P_{Reference} + 0.5\rho U^2 \tag {1}$$

Where:

• \(P_{Total}\) is the new scalar in the post-processor, representing total pressure
• \(P_{Gauge,\ static}\) is the usual gauge static pressure in the post-processor
• \(P_{Reference}\) is the Reference pressure from Figure 2. Note that one usual approach is to define here the absolute pressure of your system
• \(\rho\) is the density of the fluid
• \(U\) is the local velocity of the fluid

Pressure Coefficient

A result control for pressure coefficient can be created with the following configuration:

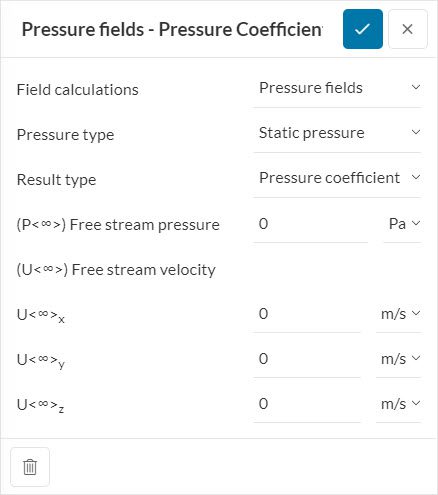
In Figure 3, the user should define their Free stream velocity based on the global coordinate system. Based on the input settings, SimScale uses the following formula to calculate the pressure coefficient \(C_p\):

$$C_p = \frac{P_{Gauge,\ static}\ – \ P_{Free\ stream}}{0.5\rho U^2} \tag {2}$$

Where:

• \(C_p\) is the pressure coefficient
• \(P_{Gauge,\ static}\) is the usual gauge static pressure in the post-processor
• \(P_{Free\ stream}\) is the free stream pressure. For incompressible analysis, this value will usually be zero Pascal
• \(\rho\) is the density of the fluid
• \(U\) is the velocity of the fluid, calculated from the Free stream velocity defined in Figure 3

Turbulence

The Turbulence result control allows the user to evaluate the yplus values in the post-processor. This parameter is very important for applications such as external aerodynamics and turbomachinery.

This result control is available for incompressible, compressible, and convective heat transfer analysis types. Note that the turbulence model must not be Laminar for the Turbulence result control to be available.

For background information on yplus and useful formulas, please check this post.

Vorticity

From a physical standpoint, one can understand vorticity as a vector having a magnitude equal to the maximum “circulation” at each point. Furthermore, the vector is oriented perpendicularly to the plane of circulation for each point¹.

In the SimScale post-processor, vorticity is represented by vectors containing components in the x, y, and z directions, as well as a magnitude.

From a mathematical perspective, vorticity is defined as the curl of the velocity vector, as in Equation 3:

$$ Vorticity = \nabla \textrm{🗙} \vec{U} \tag{3}$$

Mean Age of Fluid

The mean age of fluid result control can be used to compute the local mean age of any fluid (ex: Air or Water) in the unit of seconds. This is nothing but the time a particle takes to travel from the inlet to the outlet.

The diffusion term used to calculate the age of fluid can be enabled or disabled. When enabled, the Turbulent Schmidt number (\(Sc_{t}\)) and Diffusion coefficient \(D\) can be defined. The diffusion coefficient controls the laminar diffusion rate. For turbulent flows, the overall diffusion coefficient is calculated as:

$$\Gamma= D \rho + \frac{\mu_{eff}}{Sc_{t}} \tag{4} $$

Where \(\Gamma\) is the diffusion term, and \(\mu_{eff}\) is the effective viscosity.

Some commonly found diffusion coefficients are:

• 2.88 x 10^-5 \(m^2/s\) for Air (recommended for turbulent air flows)²
• 2.299 x 10⁻⁹ \(m^2/s\) for Water³

This result control is available for incompressible, convective heat transfer, and conjugate heat transfer v2.0 simulations. The theoretical value for the mean age of fluid is given by:

$$Mean\ age\ of\ fluid = \frac {V}{Q} \tag{5}$$

Where \(V\) is the volume of the test environment and \(Q\) is the volumetric flow rate at the inlet.

Validation Case: Mean Age of Air in a Room

Wall Shear Stress

The wall shear stress result control can be set in incompressible, compressible, convective heat transfer, and conjugate heat transfer simulations. As an output, the user obtains wall shear stress components in the x, y, and z-directions. Furthermore, the resultant vector for wall shear stress is also available.

Thermal Comfort Parameters

This result control complies with the methodology of both ASHRAE 55 and ISO 7730 Standards. By setting up a thermal comfort parameter under result control, the post-processor will contain two additional scalars:

• Predicted Percentage of Dissatisfied (PPD)
• Predicted Mean Vote (PMV)

A series of parameters may affect the PPD and PMV values, including the clothing coefficient, metabolic rate, and relative air humidity:

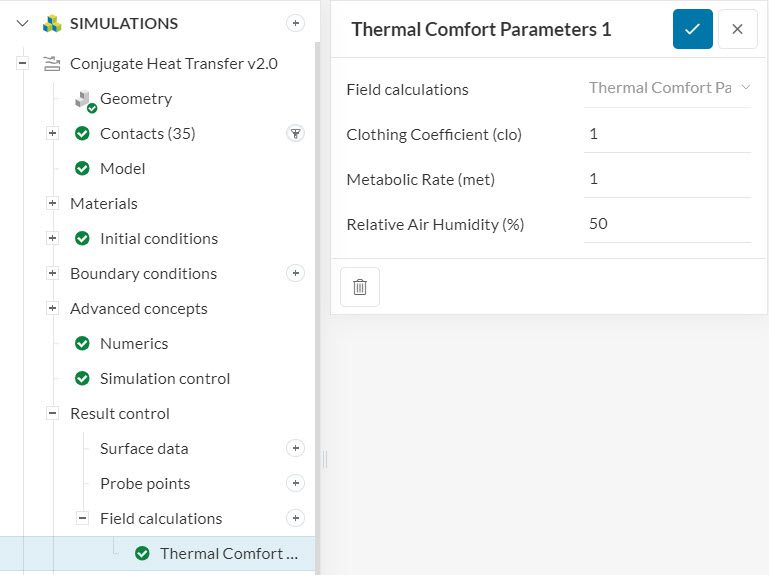
For more detailed insights about the set up of a thermal comfort parameter result control, please check this documentation page.

Friction Velocity

This field calculations result control item computes the friction velocity \(u_\tau\), which can be used to determine wall shear stress:

$$u_\tau = \sqrt\frac{\tau}{\rho} \tag {6}$$

Where \(\tau\) is the wall shear stress and \(\rho\) is the fluid density. Since both friction velocity and wall shear stress are vectors, we can rearrange equation 6 to account for the direction of the vectors when calculating wall shear stress:

$$\vec {\tau} = \rho\ mag\ (\vec{u_\tau})\vec{u_\tau} \tag{7}$$

Where \(mag\ (\vec{u_\tau})\) indicates the magnitude of the friction velocity vector.

Surface Normals

The surface normals result control is only available for the Incompressible (LBM) solver. This result control item is mostly used for further post-processing in third-party software, such as ParaView. The surface normals are not available for visualization in the SimScale post-processor.

Turbulence Fields (PWC and LBM)

Turbulent Kinetic Energy and Turbulence Intensity fields are only available in PWC / LBM simulations. Most turbulence models don’t directly simulate all turbulence scales due to computational cost. Instead, they model the effects of the smaller, unresolved scales on the larger scales. This gives rise to two types of solutions namely, Modeled and Resolved. A combined result of both these solutions is then termed as Total.

Turbulent Kinetic Energy (Modeled)

The Turbulent Kinetic Energy (Modeled) is always calculated by the solver’s turbulence model as a default solution field and is therefore not available in the fields calculation menu but can be found in the post-processor. If none of the other TKE fields are added in the Result Control, this is simply named as Turbulent Kinetic Energy.

Turbulent Kinetic Energy (Resolved)

Turbulent Kinetic Energy (Resolved) is turbulent energy that is directly resolved and captured in simulation without any modeling. In LES, the large turbulent eddies are directly resolved by the simulation, and only the smaller, sub-grid scale turbulence is modeled.

Turbulent Kinetic Energy (Total)

Turbulent Kinetic Energy (Total) includes both modeled and resolved turbulence. This is the total energy in the turbulence, combining both the energy from the larger resolved eddies and the smaller, unresolved eddies that are modeled.

There are again three components to Turbulence Intensity similar to Turbulent Kinetic Energy:

Turbulence Intensity (Modeled)

The turbulence intensity gives the level of turbulence and can be defined as follows:
$$I = \frac { u’ }{ U }$$
where \(u’\) is the root-mean-square of the turbulent velocity fluctuations. Learn more.

Turbulence Intensity (Modeled) corresponds to the portion of the turbulence intensity that is modeled using a turbulence model, such as in RANS or the sub-grid scale (SGS) model in LES.

Turbulence Intensity (Resolved)

This turbulence intensity is associated with the resolved turbulent eddies, i.e., large-scale turbulent structures that are directly simulated.

Turbulence Intensity (Total)

The total turbulence intensity includes contributions from both the resolved and modeled components.

Wall Heat Flux

This field calculation is available in CHT v2.0 and IBM simulations. It retrieves the heat flux (units of power per surface area (\(W/m^2\))) at each interface and boundary wall of the model. Also, it has the option to automatically compute useful quantities that describe the heat transfer, such as the Heat transfer coefficient and the Nusselt Number:

1. Heat transfer coefficient: It toggles the computation of the proportionality constant relating the heat flux at one point of the surface of a solid with the difference between the temperature at the given point and a Reference temperature.
2. Reference temperature: It is a method to select the temperature used to compute the heat transfer coefficient, between sampling the Wall adjacent cell from the simulation results, or entering a Fixed value.
3. Nusselt Number: It toggles the computation of the ratio between convective and conductive heat transfer at the interface. A Reference length parameter is needed to be input for the computation of this quantity.
4. Reference length: It is the characteristic dimension of the fluid domain, used to compute the Nusselt number. The reference length should ideally be taken in the direction of the surface normal (for example the diameter of a sphere or cylinder), but for complex shapes, the volume-to-surface-area ratio can be used.

The heat transfer coefficient (\(h\)) appears in the convective heat transfer equation (Newton’s law of cooling), relating the heat flux (\(Q\)) and the temperature difference with the reference value (\(T_{ref}\)):

$$ Q = h A_s(T_s – T_{ref}) \tag{8}$$

The Nusselt number \(Nu\) can be related to the heat transfer coefficient \(h\), the reference length \(L\) and the thermal conductivity \(\kappa\):

$$ Nu = \frac{Convective Heat Transfer}{Conductive Heat Transfer} = \frac{ h L }{ \kappa} \tag{9}$$

Please notice that the Heat transfer coefficient and the Nusselt number are properties related to the heat transfer in the flow, and as such will only be computed for fluid regions, not for solid regions.

Mean Radiant Temperature

Mean radiant temperature is a field calculation exclusively available in conjugate heat transfer v2.0 simulations. This field calculation allows the calculation of local mean radiant temperature values if solar load is disabled.

The mean radiant temperature values are used for PMV and PPD calculations, which are related to the thermal comfort parameter result control. Therefore, with a mean radiant temperature result control in place, you can obtain more precise PMV and PPD values.

You will find more information involving mean radiant temperature, as well as equations, in this documentation page.

Operative Temperature

The operative temperature combines the air temperature with the mean radiant temperature to provide an overall measure of thermal comfort, with the formulation described here.

This result control is only available for conjugate heat transfer v2.0 simulations.

Last updated: October 29th, 2024