Documentation
Heating, Ventilation, and Air Conditioning (HVAC) systems account for a substantial percentage of energy consumption in buildings. The size of the system is a critical factor, as systems that are either too large or too small for a building’s requirements can lead to excessive energy use. Correctly sizing the HVAC system based on the building’s square footage, insulation, climate, occupancy levels, and geography is essential for achieving optimal energy efficiency. Additionally, factors such as system size, age, maintenance practices, building design, and geographical location further influence energy usage.
Analytical approaches to select heating or cooling systems only consider simple air movements and simple room conditions. Often this approach is combined with ASHRAE guidelines and energy modeling tools to predict the overall energy usage and performance of a building or HVAC system. In contrast, CFD considers the geometry of the space, boundary conditions, and the physics of fluid dynamics in a more granular manner. CFD can bring a lot of value in terms of local effects predominantly in studying fluid dynamics, thermal behavior, and air quality within a space. It is often employed in the design of ventilation systems, understanding indoor air quality, and assessing thermal comfort. These local characteristics can provide detailed insights, assisting engineers and designers in:
In this article, we will explore the concepts of mean radiant temperature and operative temperature and how they are estimated and analyzed using CFD for thermal comfort.
The concept of temperature, a fundamental parameter indicating the average kinetic energy of particles in a substance, provides a general gauge of the thermal conditions in a given space. In general, the temperature value we see on measurement devices denotes the Air Temperature, which is the average temperature of the air surrounding an object (an occupant in terms of thermal comfort). The average is with respect to location and time. According to ASHRAE 55 standards, the spatial average is the numerical average of the air temperature at the ankle level, the waist level, and the head level. These levels are 0.1, 0.6, and 1.1 \(m\) (4, 24, and 43 in.), respectively, for seated occupants, and 0.1, 1.1, and 1.7 \(m\) (4, 43, and 67 in.) for standing occupants. [ASHRAE 55]
Understanding and optimizing thermal comfort encompasses various temperature metrics that go beyond the conventional measure of ambient air temperature. Key temperature metrics used in thermal comfort include:
Radiation has a greater effect on thermal sensation. Encountering localized cold/hot surfaces is a common situation during building construction, giving rise to frequent considerations about radiative symmetry and operative temperature. The issue of uneven temperature distribution, especially concerning nearby surfaces, is a recurring concern. This scenario often triggers a thorough examination of radiative symmetry, highlighting the importance of achieving balance in thermal conditions across different zones within a building. Discussions about operative temperature, which incorporates both air and radiant temperatures, become pivotal in addressing and resolving such challenges. In the context of building construction, the need to navigate and optimize these factors emerged consistently, highlighting the significance of comprehensive solutions for achieving thermal comfort and efficiency.
Here is an example Scenario where radiant temperature is critical. Radiant heat is transferred from a hot object to a colder object without affecting (heating) the space and air in between. A person’s body temp is between 36 \(ºC\) and 37 \(ºC\). If the air-conditioned room temp is about 24 \(ºC\), then the person’s external skin temp will average about 30 \(ºC\). All hot objects above 30 \(ºC\) will transfer heat by radiation to the person without heating up the air in between which will remain at 24 \(ºC\).
Other scenarios include:
Mean radiant temperature (MRT) is a measure of the average temperature of all surfaces surrounding a person, including walls, floors, and objects. Unlike air temperature, MRT considers the radiant heat exchange between the human body and its surroundings. This is crucial because humans don’t just exchange heat with the air; they also gain or lose heat through radiation to and from nearby surfaces.
Mean Radiant Temperature is calculated using:
$$ MRT = \frac{\Sigma (T_i \times F_i)}{\Sigma F_i} $$
Where:
Operative temperature is an overall measure of thermal comfort that combines air temperature and mean radiant temperature. It is the average of the air temperature and the mean radiant temperature weighted, respectively, by the convective heat transfer coefficient and the linearized radiant heat transfer coefficient for the occupant [ASHRAE 55]. In other words, the operative temperature is defined as the uniform temperature of an enclosure where a person would exchange the same amount of heat by radiation plus convection as in the actual non-uniform environment [ISO EN 7730].
Operative temperature can be derived using the following formula:
$$ t_o = \frac{(t_{mr} + (t_a \times \sqrt{10v}))}{1 + \sqrt{10v}}$$
Where:
The operative temperature of a system can be estimated using the Mean Radiant Temperature (MRT) and the air temperature. The formula for estimating the operative temperature (\(T_O)\) based on MRT and air temperature (\(T_air)\) is often used in the field of thermal comfort and building science. The formula is as follows:
$$ T_o = MRT + (0.5 \times \Delta T) $$
Where:
Note
This formula assumes that the environment is uniform in terms of air temperature and radiant temperature. If the radiant temperature varies significantly within the environment, this simple formula may not be accurate, and more complex calculations may be required.
By default Mean Radiant Temperature is approximated as a single uniform scalar value throughout the domain, based on a size-weighted average across all domain surface temperatures.
In simulations with the conjugate heat transfer v2.0 without solar load, you can request for the calculation of local mean radiant temperatures and local operative temperatures by creating the corresponding result controls under field calculations.
The MRT is then used to calculate the thermal comfort parameters like Predicted Mean Vote (PMV) and Percentage of People Dissatisfied (PPD). The approximation does not take into account view factors and assumes an emissivity of 1.
With the enhanced implementation, MRT is now calculated taking into account the view factor and local surface temperature in the vicinity of the considered object as per the mean radiant temperature equation mentioned above.
Note
Currently, the local Mean Radiant Temperature and Operative temperature are available only under CHTv2 analysis type. Calculation of MRT with Solar Radiation is not yet supported.
Note
In SimScale, the default temperature field denotes the average Air temperature of the fluid.
This case study shows a clear difference between Standard air temperature and Operative temperature. In this study, a typical room (dimensions 5 \(m\) * 3 \(m\) * 3 \(m\)) with two occupants, an HVAC supply, and an open window is considered.
For a supply inlet of 0.39 \(m^3/s\) at 18 ºC and 450 \(W/m^2\) radiator load, the average air temperature near the occupants was between 19 \(ºC\) and 20 \(ºC\). Whereas in reality, the occupant standing near the radiator should feel hotter than the one standing away from it. These details on thermal sensations can be captured by the radiant temperature as shown in Figure 5.
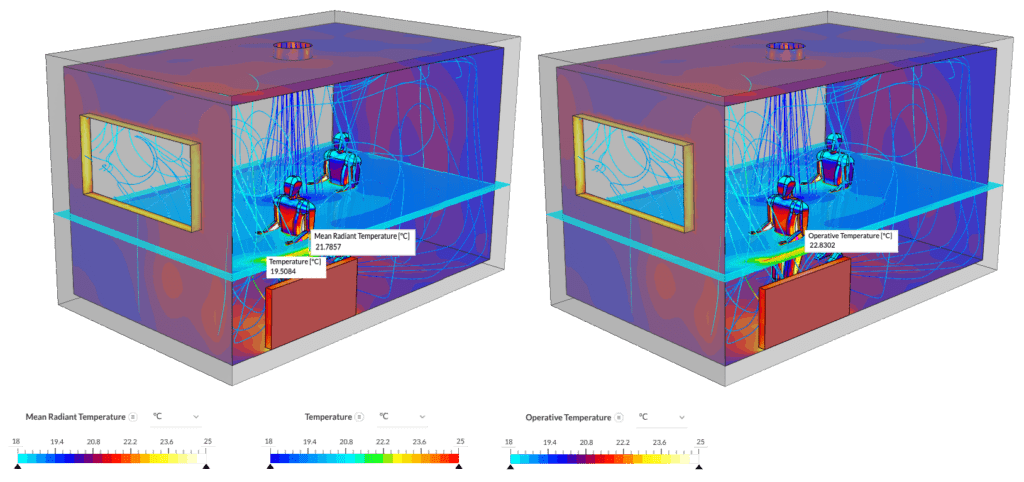
An overview of all thermal comfort parameters used in SimScale can be found in our documentation article on Thermal Comfort Parameters.
References
Last updated: September 6th, 2024
We appreciate and value your feedback.
What's Next
What Is FEA | Finite Element Analysis?Sign up for SimScale
and start simulating now