Documentation
Fick’s law describes the movement of particles from a region of high concentration to a region of lower concentration. This process, known as diffusion, occurs independent of bulk flow, which is the movement of flow due to a pressure gradient.
Simulating diffusion within a fluid is often referred to as scalar mixing or passive species. The core assumption of passive species mixing is that the species that are transported within the fluid do not have an effect on the fluid flow. One common analogy that can be used is the use of dye injection into a fluid stream to visualize the flow pattern. The injection of dye into a fluid stream is a common approach used in research and academia.
On a more practical level, passive species mixing is often used as an approximation to understand how two similar fluids mix. For example, air and carbon monoxide have very similar material properties such that the mixing of these two gases can be approximated within SimScale with incompressible flow and passive species mixing.
Material Properties of Air and CO at STP (T = 0° C, P = 0.101 MPA)
| Material | Density (kg/m3) | Dynamic Viscosity (Pa x s) |
| Air | 1.29 | 1.72 x 10-5 |
| CO | 1.25 | 1.66 x 10-5 |
Adolf Fick, who is responsible for defining Fick’s laws, first started doing experiments on diffusion during the mid-19th century. Fick’s experiments consisted of measuring the concentrations and gradients of salt between two fluid reservoirs. Although he predominantly performed experiments with fluids, his law is used today to define diffusion in solids, liquids, and gases.
Fick’s laws are now used to define the majority of our understanding of diffusion in solids, liquids, and gases. In the rare case that a diffusion process does not follow Fick’s laws, it is called “non-Fickian diffusion”.
Fick’s first law relates the diffusive flux within a medium to the gradient of the concentration. It states the flux goes from regions of high concentration to regions of low concentration, and the concentration is linearly proportional to the spatial derivative. In other words, the solute will move from a region of high concentration to a region of low concentration across a linear concentration gradient4.
The most typical form assumes one spatial direction and is in a molar basis2:
$$J = -D\frac{d \varphi}{dx}\tag{1}$$
where:
J = diffusion flux. J measures the amount of substance that will flow through a unit area per unit time
D = diffusion coefficient (area per unit time)
\(\varphi\) = concentration (amount of substance per unit volume)
x = position
Fick’s second law defines how diffusion causes the concentration to change with respect to time4. It is a partial differential equation that reads (1 dimension):
$$\frac{\delta \varphi}{\delta t} = D\frac{\delta^2 \varphi}{\delta x^2}\tag{2}$$
where:
\(\varphi\) = concentration in dimensions [(amount of substance) x length-3], (example: mol/m3)
t = time
D = diffusion coefficient (area per unit time)
x = position
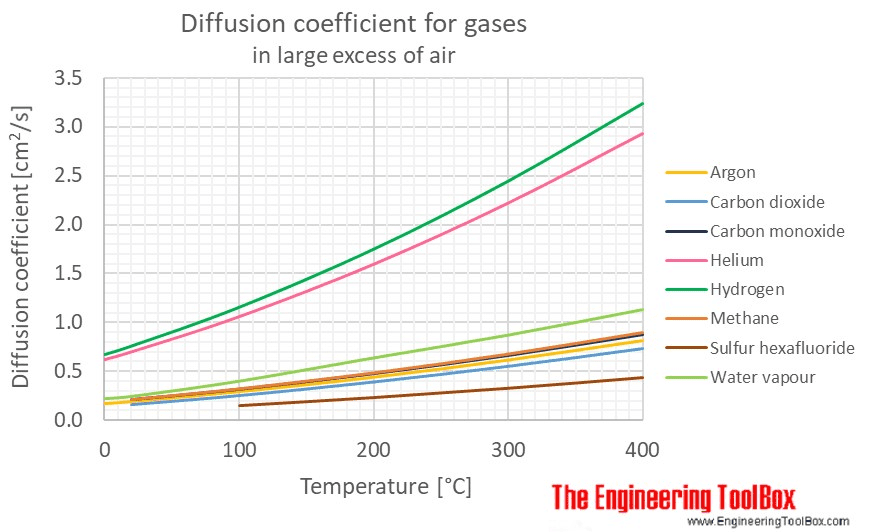
The diffusion coefficient is a constant describing how quickly a pair of species diffuse into each other. The higher the diffusivity, the faster the species diffuse into each other. It has units of \(\frac{\text{length}^2}{time}\), and the most common units are \(\frac{m^2}{s}\) or \(\frac{cm^2}{s}\).
Diffusion coefficients for pairs of species are empirically derived and well-known for common fluids. For example, Engineering Toolbox lists diffusion coefficients for common gases like argon, methane, carbon dioxide, carbon monoxide, etc, and air.
Diffusion simulation capabilities are currently supported in the Incompressible, Convective Heat Transfer, and Conjugate Heat Transfer v2.0 analysis types. Within all of these analysis types, diffusion can be enabled by setting the “Passive species” option to something higher than 0. SimScale is currently capable of simulating the diffusion of up to 10 different passive species. The diffusion coefficient is defined in the simulation tree under “Model” and the default value is \(1e^{-5} \frac{m^2}{s}\).
The SimScale public projects library provides a large number of projects which model diffusion via SimScale’s scalar mixing capabilities. In addition, scalar mixing is used in both the “Smoke Propagation From a Chimney” and “Car Park Contamination Simulation” tutorials.
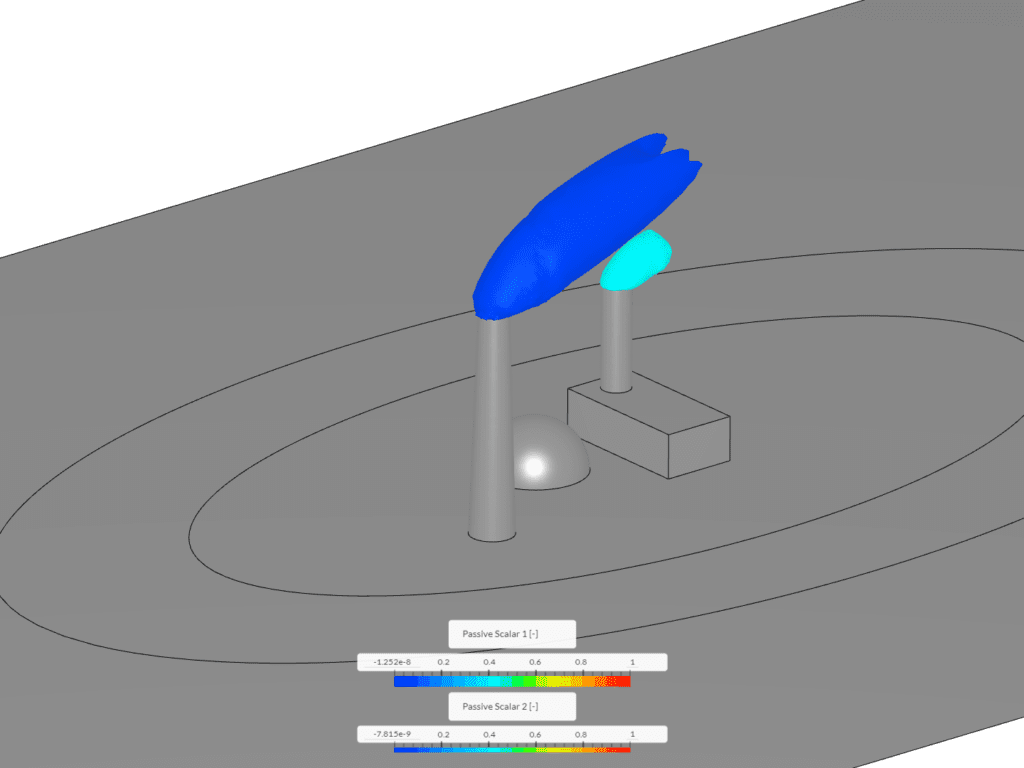
Example 1 shows an isovolume of scalar between 0.1 and 1. This image was created via the “Smoke Propagation From a Chimney” tutorial. In this context, scalar 1 and scalar 2 represent exhaust discharging from a smokestack and building and mixing with the surrounding air.
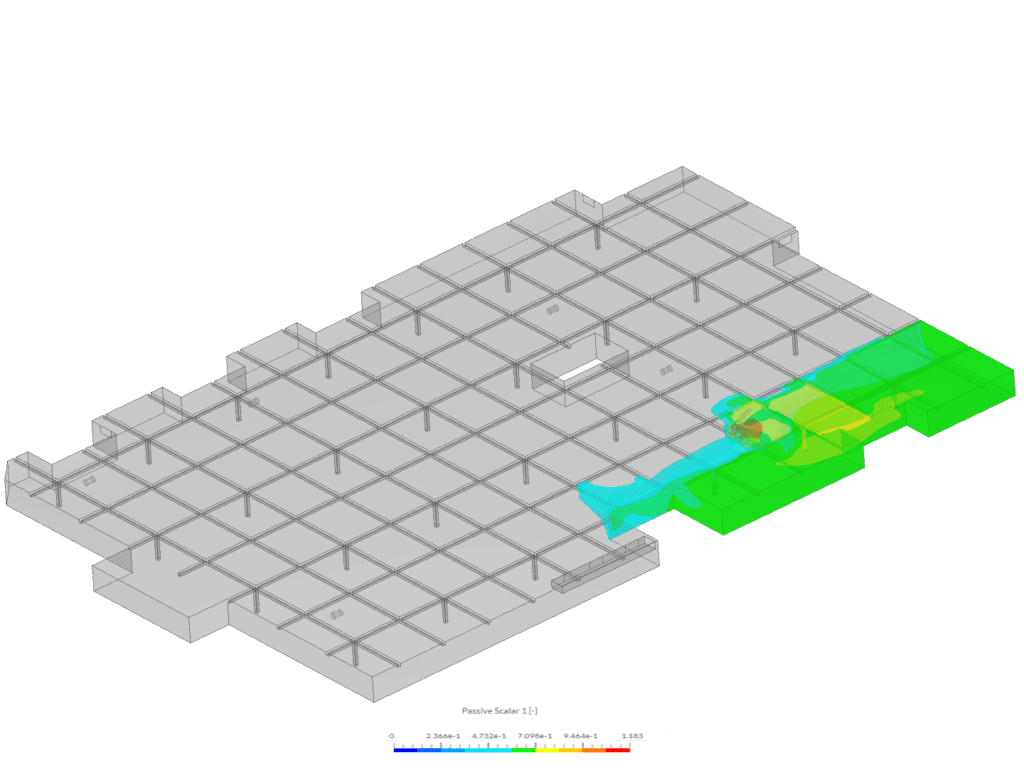
Example 2 shows an isovolume of scalar between 0.5 and 1.183. This image was created via the “Car Park Contamination” tutorial. In this case, scalar 1 represents carbon monoxide exhaust from a car in an underground car park.
References
Last updated: August 11th, 2023
We appreciate and value your feedback.
What's Next
Indoor HumiditySign up for SimScale
and start simulating now