Documentation
A purely plastic material model describes the material behavior after the onset of plasticity. At this point, the solid materials will undergo irreversible deformation when subjected to loading. For example, a solid metal being shaped by bending or pounding.
In reality, most of the materials have an elastic and a plastic region separated by a yield point, after which the stress-strain curve becomes nonlinear. A typical stress-strain curve for steel is shown below:
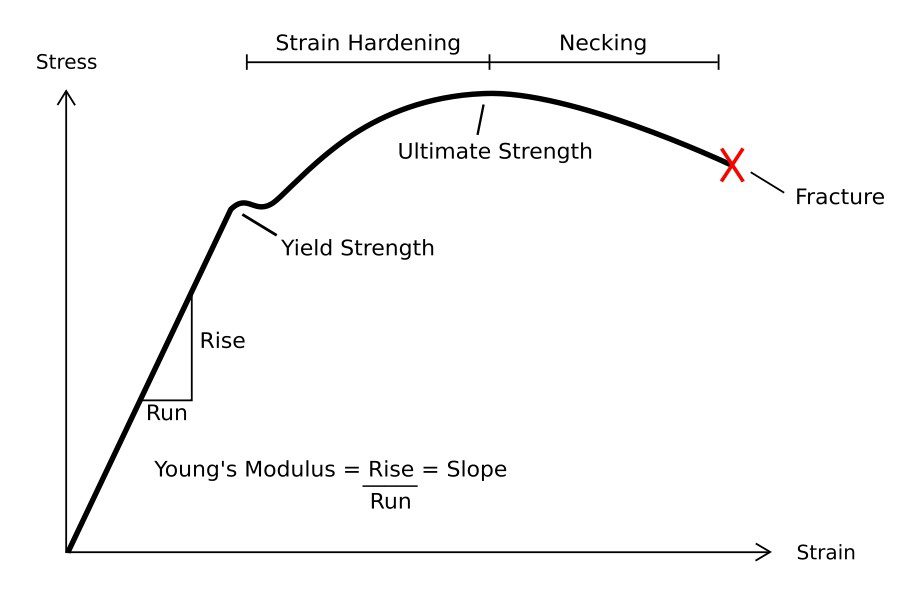
That is why SimScale allows you to model such materials as elasto-plastic materials. The Elasto-plastic material model has a wide variety of applications, thus it is particularly useful for predicting the behavior of materials under extreme conditions, such as impact loading, high pressures, and high temperatures.
There are also applications where some plastic deformation is allowed in the design. In such cases, first run a simulation using a linear elastic behavior for the materials. If the stresses are greater than the yield strength, then an additional analysis is done with a plastic material behavior.
Important
An elasto-plastic material behavior can only be defined for the following analysis types:
– Nonlinear static analysis;
– Dynamic analysis;
– Nonlinear thermomechanical analysis.
A material which undergoes an elasto-plastic regime can be modeled either as Multilinear or Bilinear.
Modeling the material as multilinear means establishing its properties as being the same as the stress-strain curve obtained from a tensile test. In this model, the strain hardening curve is plotted by some linear lines tangent to the nonlinear behavior. Therefore, in multilinear modeling the material behaves as closely as possible to reality.
The bilinear hardening model is similar to the multilinear model, but it does not take into account the entire behavioral history of the material. This model is also described by the stress-strain curve, where the coefficients needed for material characterization are the Young modulus, and the plastic phase modulus, where the second one cannot be less than zero, neither greater than the Young modulus. When the plastic phase modulus comprises 99% of the Young modulus, the bilinear model simulates a linear elastic analysis. If the plastic phase modulus is 1% and/or 0, the bilinear model simulates the behavior of perfect plasticity.

As shown in Figure 2, the bilinear elasto-plastic model can be assumed to be sufficient to predict the behavior of materials when there is no complexity in terms of geometries and loadings in the simulation.
Quick Tip
The bilinear material model provides a handy modeling tool with a good approach, once it is simple and quick. However, if you need to be more accurate, or if you have a complex model, prefer to use multilinear.
Notwithstanding, once you have chosen the bilinear elasto-plastic model, SimScale also provides perfect plasticity as an option for the hardening model. In general, perfect plasticity is a simplification of the actual material behavior, and it is only applicable under 2 situations:
While most material parameters in practice are provided as engineering stress-strain, SimScale requires true stress-strain material properties to accurately cope with the thinning of the material.
Engineering vs. True Stress Strain
For ductile materials, thinning of the probe during material test can occur. Since stress is calculated as $$ Stress=\frac{Force}{Cross \ section} = \frac{N}{m^2} \tag{1}$$ two material parameters can be obtained. Engineering stress, which uses the initial cross-section as a reference, and true stress, which uses the true cross-section of the material.
To convert the engineering stress-strain data to true stress-strain the following formulas shall be used.
\( \sigma_t = \sigma_e*(1+\varepsilon_e) \tag{2} \)
\( \varepsilon_t = ln(1+\varepsilon_e) \tag{3} \)
Where,
\( \sigma_t \) = true stress
\( \varepsilon_t \) = true strain
\( \sigma_e \) = engineering stress
\( \varepsilon_e \) = engineering strain
\(ln\) = natural log
In addition sometimes instead of engineering stress-strain curve the material data is provided as true stress-plastic strain curve. In such a case, this also needs to be converted to true stress – true strain. The following formula 4 can be used to convert this data.
\( \displaystyle \varepsilon_t = \varepsilon_p + \frac{\sigma_t}{E} \tag{4} \)
Where,
\( \varepsilon_p \) = plastic strain
\( E \) = Young’s Modulus
To define an elasto-plastic material, follow the steps given below:

From Figure 4 it is possible to see a real stress-strain curve given by a tensile test in a sample with the obtained values shown in Figure 6.
Once the user has chosen a multilinear model, a series of data points over the stress-strain curve and its coordinates are defined. These points can be manually input. Alternatively, it’s also possible to create a comma-separated .csv file in any text editor, containing the point coordinates in this format (no spaces after the comma): strain, stress. This .csv file can be uploaded to SimScale.
Important
When using the multilinear model, the first point of the series is taken as the yield point by the solver. Using Figure 4 as reference, this would be the structure of the .csv file:
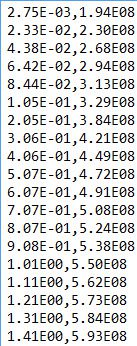
To capture the stress-strain curve appropriately, make sure to add enough data points. Between two points, the values are linearly interpolated.
After saving the stress-strain curve, adjust Young’s modulus according to the stress-strain data. Young’s modulus is given by dividing the stress and strain values at the yield point:
$$E = \displaystyle \frac {\sigma_{yield}}{\varepsilon_{yield}} \tag {5}$$
After inputting the values from our example in equation (5), we have:
$$ \displaystyle E = \frac {1.94e8}{2.75e(-3)} = 7.05e10 \ Pa \tag {6}$$
A wrongly calculated value for Young’s modulus may lead to a diverged solution.
Note
This model is not a suitable choice for brittle materials such as ceramics and concrete. It is only applicable for ductile and isotropic materials, such as aluminum and steel.
Last updated: June 19th, 2024
We appreciate and value your feedback.
Sign up for SimScale
and start simulating now