Young’s Modulus

Young’s modulus or elastic modulus is a mechanical property of linear elastic solid materials. It defines the relationship between stress and strain in a solid material, and is given by:

$$ \sigma = E \varepsilon $$

where,

• \(E\) is Young’s modulus of the material,
• \(\sigma\) is the stress, and
• \(\varepsilon\) is the strain.

Young’s modulus has units of pressure or stress (\(Pa, psi \)) since the strain is a dimensionless quantity. From the given relation, it can be seen that the elastic modulus is the ratio between stress and strain:

$$ E = \frac{ \sigma }{ \varepsilon } $$

Physically speaking, it is a measure of how rigid a material is. As the overall rigidity of a part is also dependent on the geometrical shape, it is necessary to have a shape-independent property to measure the material.

Young’s Modulus in Linear Elastic Materials

A solid material is called elastic if it is able to naturally return to its original shape after the applied loads are removed. On the other hand, if the ratio between stress and strain is constant during the deformation process, then Young’s modulus is also a constant, and the material is considered to be linear elastic.

Workbench Setup for Linear Elastic Materials

When setting up a structural simulation, Young’s modulus parameter for a linear elastic material must be specified as follows:

Learn more about linear elastic materials in the following document:

Linear Elastic Materials

Young’s Modulus in Nonlinear Materials

In general, all solid materials are not linear elastic, especially when they are subjected to high levels of deformation. Figure 2 shows an example stress-strain curve for a ductile carbon steel material, as obtained from a uniaxial tension test:

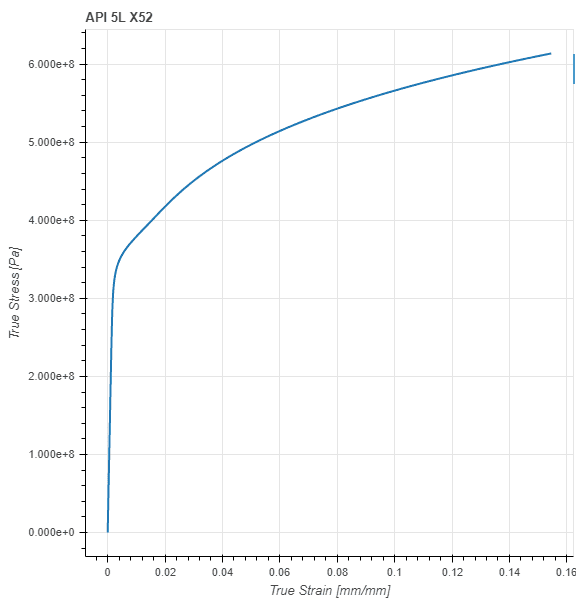
It can be seen that the material has a linear elastic behavior only for small strain values. When deformation increases, nonlinear behavior starts to occur. In this case, the ductile material exhibits plasticity, but other nonlinearities such as hyperelasticity or fragile rupture can also occur.

In general, most materials can be approximated to be linear elastic under the assumption of small deformation. In that case, the elastic modulus can be approximated by analyzing the linear portion of the stress-strain curve, and computing:

$$ E_y = \frac{ \sigma_y }{ \epsilon_y } $$

where,

• \( E_y \) is the linear elastic Young’s modulus approximation,
• \( \sigma_y \) is the stress value at the elastic limit (end of the straight line), and
• \( \varepsilon_y \) is the strain value at the elastic limit.

Workbench Setup for Elasto-Plastic Materials

When setting up a structural simulation, Young’s modulus parameter for an elasto-plastic material must be specified as follows:

Learn more about elasto-plastic materials in the following document:

Elasto-plastic Materials

Last updated: September 27th, 2021