Documentation
Natural frequency is the rate at which a body vibrates when disturbed without being subject to a driving or damping force. The pattern or shape of this vibrating motion is the corresponding mode of the body’s or system’s vibration, known as the normal mode. Vibrating objects can have one or more normal modes, depending on how they’re initially disturbed. Each normal mode has a corresponding natural frequency associated with it. These two attributes compose the fundamental dynamic properties of the system.
A system or object can oscillate or vibrate at any arbitrary rate depending on the external force driving its motion:
These frequencies that the systems vibrate at are called the forced frequencies, and they vary based on the loading conditions applied to the system. For engineers, understanding a structure’s natural frequency is crucial to ensure it doesn’t operate under conditions that may cause resonance. Resonance is when the forced frequency of an undamped body equals its natural frequency.
For any structure, there is a loading or forced frequency that results in ever-increasing oscillatory amplitude responses. This forced frequency leading to such a runaway oscillatory response is called the resonant frequency, and it’s related to the natural frequency of the system. For systems that don’t have any damping measures, the resonant frequency is equal to the natural frequency.
Structures undergoing resonant-frequency-loading conditions can fail as this force amplitude rises over time. There are many catastrophic examples of this occurring in history; a famous example was the Tacoma Narrows Bridge collapse in 1940.
The construction of the bridge’s structure failed to account for the possible wind-loading conditions, which resulted in a significant oscillation of the bridge around its natural frequency. Five months later, the bridge’s suspension system failed under these drastic oscillations, causing the entire bridge to collapse.
Harmonic oscillators are great at modeling vibrational motion. The basic principle of a harmonic oscillator system is that the body experiences a restoring force (F) proportional to the displacement from its equilibrium position. The equation for a simple harmonic oscillator is:
$$ F=-kx $$
where:
k is the positive stiffness constant of the system expressed in units such as N/m
x is the displacement of the center of mass of the system
A common example of a basic harmonic oscillator is the mass-spring system. This system is the most fundamental vibrating system to model oscillatory behavior. As the mass is displaced from its equilibrium position, the spring reacts with a force proportional to the amount of displacement it has extended or compressed to move the mass about the equilibrium position.
To determine a dynamic system’s natural frequency, eigenvalue analysis can be performed to obtain the natural frequency. Eigenvalue Analysis is the mathematical operation that solves for the dynamic properties of a system using its characteristic equation, composed of the system’s stiffness and mass distribution. For a basic harmonic oscillator, eigenvalue analysis can be trivial using fundamental formulas from linear algebra to determine the system’s natural frequency.
Using the same mass-spring system above, the formula for natural frequency (\(\omega_{n})\) in radians per second is as follows:
$$ \omega_{n} = \sqrt{\frac{k}{m}} $$
A dynamic system can often have damping effects, such as friction, air resistance or an actuator. In general, a damper serves to reduce the peak amplitude of the oscillatory responses of any vibration while shifting the system’s natural frequency down. This is done by reducing the magnitude of the restoring force on an oscillating system.
Adding a damper to a simple harmonic oscillator model makes it a damped harmonic oscillator; the damper reduces the magnitude of the restoring force proportional to the velocity of the center of mass. In a spring-mass-damper dynamic system, the restoring force (F) can be modeled by the following formula:
$$ F=-kx -cv $$
where:
c is the positive damping coefficient of the damper, expressed in units such as N-s/m
v is the velocity of the center of mass of the system
The natural frequency of a damped system is reduced compared to its undamped counterpart. This is due to the damping force reducing the acceleration of the center of mass towards the equilibrium position, making oscillations slower and less frequent. The dimensionless measure of the system’s damping relates its stiffness, mass and damping to a ratio called the Damping Ratio. The Damping Ratio (\(\zeta)\) formula is as follows:
$$ \zeta = \frac{c}{2\sqrt{km}} $$
The damping ratio gives a quick insight into what the frequency response will look like on a dynamic system after an initial disturbance from its equilibrium position. Only in underdamped or undamped systems, where the damping ratio is less than 1, will the system oscillate about the equilibrium position. An underdamped system’s natural frequency is shifted based on the damping ratio; this damped natural frequency (\(\omega_{d}\)) can be calculated using the following formula:
$$ \omega_{d} = \omega_{n} \sqrt{1-\zeta^2} $$
The shift in the natural frequency based on the damping ratio is visualized below; the plot below shows the steady-state amplitude response of a system undergoing forced vibration, where the x-axis represents the ratio between the forced frequency and the undamped system’s natural frequency.
The frequency associated with the peak amplitude indicates the respective case’s resonant frequency, which is equal to the natural frequency. Note that as the damping ratio increases, the forced frequency that causes a peak amplitude response is shifted lower, indicating a reduced natural/resonant frequency.
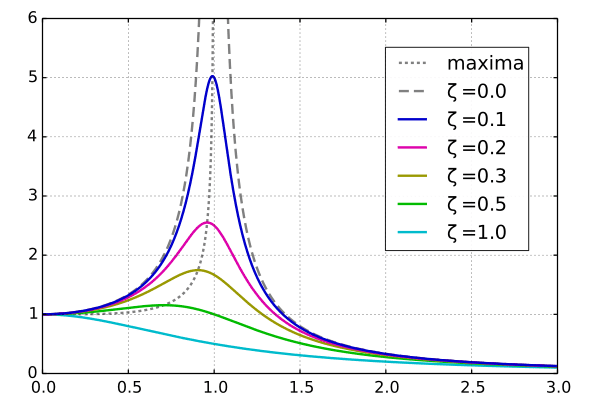
Most parts or assemblies that engineers design and work with cannot be modeled as basic harmonic oscillators like this mass-spring system, which is considered a linear system; however, the relations in the natural frequency formula above can be applied to more complex systems.
To shift the natural frequency of a system, you can either change the stiffness of the system, change the mass or dampen the system. The stiffness of a system is dictated by its shape, distribution of material, and size.
The natural frequency of a complex system can be obtained by deploying a simulation. Using Finite Element Analysis (FEA) methods, the complex geometries are discretized into a series of thousands or millions of basic linear or nonlinear systems to solve for the dynamics properties, like the natural frequencies, resonant frequencies and normal modes of the overall part/assembly.
SimScale provides the simulation technology on the platform to determine these dynamic properties within the Frequency analysis type, which determines the different modes of vibration and their associated natural frequency. Engineers can also simulate periodic loading conditions that induce forced frequency vibrations to assess how a design performs under these kinds of loading conditions within the Harmonic analysis type on the SimScale platform.
Below, you can see the results of a Frequency Analysis simulation, where the harmonic loads of concern come from the wind and associated vortex-shedding effects.
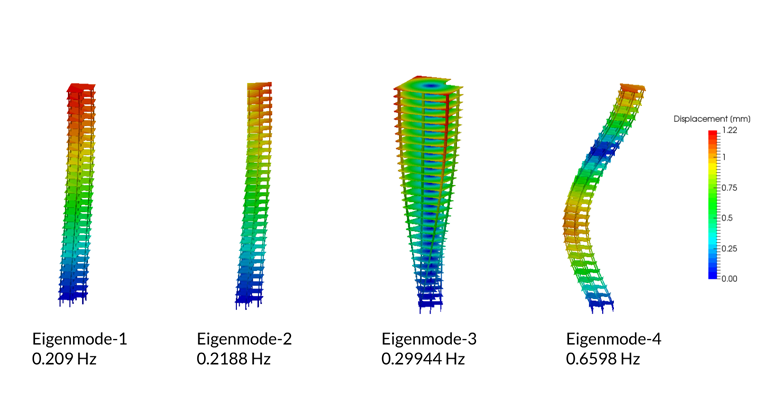
Performing these simulation analyses can give you insight into whether your designs will meet safety requirements, industry-specific codes or standards or if the part will simply fail altogether. They also give you insight such as displacement and stress distributions across the part or assembly, allowing you to quickly gain insight on how to iterate on your structural designs to make them more resilient under the given loading conditions. Often, these design iterations take you back to shifting the structure’s natural frequency and mitigating the strength of these runaway resonant responses.
To learn more about SimScale’s simulation capabilities in its Frequency & Harmonic analysis types, check out the documentation pages for the respective analysis type (Frequency Analysis and Harmonic Analysis).
The natural frequency is the frequency at which a system oscillates after an initial disturbance from its equilibrium position.
The forced frequency is the frequency at which a system vibrates due to an external oscillating force at the same frequency.
The resonance frequency is the forced frequency a system undergoes that causes growing amplitudes of oscillatory behavior. It is equal to the natural frequency.
The restoring force is the overall force that acts towards a harmonic system’s equilibrium position.
A simple harmonic oscillator is a dynamic system that, when displaced from its equilibrium position, will exhibit a restoring force proportional to the displacement, moving in a constant sinusoidal pattern when not driven by external forces.
A damped harmonic oscillator is a dynamic system that, when displaced from its equilibrium position, will exhibit a restoring force proportional to the displacement, moving in a sinusoidal pattern with exponentially decreasing amplitudes of oscillations.
The stiffness constant is the ratio between the restoring force applied to a simple harmonic oscillator system and the displacement of the center of mass.
The damping coefficient is the ratio between the damper’s contribution to the restoring force of a damped harmonic oscillator and the velocity of the center of mass.
An eigenvalue analysis is an analysis used to obtain the natural frequency of a harmonic system.
References
Last updated: August 11th, 2023
We appreciate and value your feedback.
What's Next
What Is Heat Transfer?Sign up for SimScale
and start simulating now