Validation Case: Natural Convection Between Horizontal Concentric Cylinders

This validation case belongs to CFD, more specifically to the Convective Heat Transfer solver. The reference experiment by Kuehn and Goldstein\(^1\) studies the natural convection between two horizontal concentric cylinders.

The test case aims to validate the following parameters:

• Convective heat transfer
• Natural convection

The simulation project containing the CFD model and the results can be accessed by using the following link:

Geometry

The geometrical model captures the air portion between the two concentric cylinders, to mimic the physical setup performed in the experiment of reference\(^1\). Figure 1 shows a translucent view of the model where the geometry can be appreciated:

The relevant dimensions used for the geometry and simulation are as follows:

• Length: \(L=\) 500 \(mm\)
• Radius of inner cylinder: \(R_i=\) 17.8 \(mm\)
• Radius of outer cylinder: \(R_o=\) 46.25 \(mm\)

Analysis Type and Mesh

Tool Type: OpenFOAM®

Analysis Type: Steady-state, incompressible, laminar Convective heat transfer

Mesh and Element Types:

SimScale’s Standard meshing algorithm was used for the creation of the mesh. This algorithm implements a strategy with a surface triangulation, followed by a transition layer of tetrahedrals and prisms, and finally a hexahedral core for the gross region of the flow field.

The mesh has a total of 1387582 volumetric elements, which are tetrahedrals, prisms, and hexahedrals. The triangular surface mesh can be appreciated in Figure 2, while Figure 3 shows a mesh clip to appreciate the hex core and the transition layer. It can be seen also that, in spite of implementing a laminar turbulence model, boundary layers are also included in the mesh.

Simulation Setup

Fluid Material Properties:

• Material: Air
• Kinematic viscosity (\(\nu\)): 1.529e-5 \(m^2/s\)
• Density (\(\rho\)): 1.196 \(kg/m^3\)
• Thermal expansion coefficient (\(\alpha\)): 3.43e-3 \(1/K\)
• Laminar Prandtl number: 0.713
• Specific heat: 1004 \(J/(kg \cdot K)\)

Boundary Conditions:

• Inner, Hot Wall: Fixed temperature of 347 \(K\)
• Outer, Cold Wall: Fixed temperature of 327 \(K\)
• End walls: Adiabatic

Initial Conditions:

• Uniform temperature of 293 \(K\) in the fluid region

Model:

• Gravity in the \(-g_z\) direction with magnitude 9.81 \(m/s^2\)

Results

For the comparison of results, the radial distribution of the temperature at different polar angles is presented in the reference work. The radial coordinates and temperature are normalized to be dimensionless according to the following relations:

$$\hat{R} = \frac{R – R_i}{R_o – R_i} $$

$$\hat{T} = \frac{T – T_o}{T_i – T_o} $$

For comparison, the dimensionless radius and temperature are measured at polar angles of \(\theta = 0°\) and \(\theta = 180°\), with the direction of gravity coinciding with the latter set. Figure 4 shows a comparison of the results with respect to the reference work.

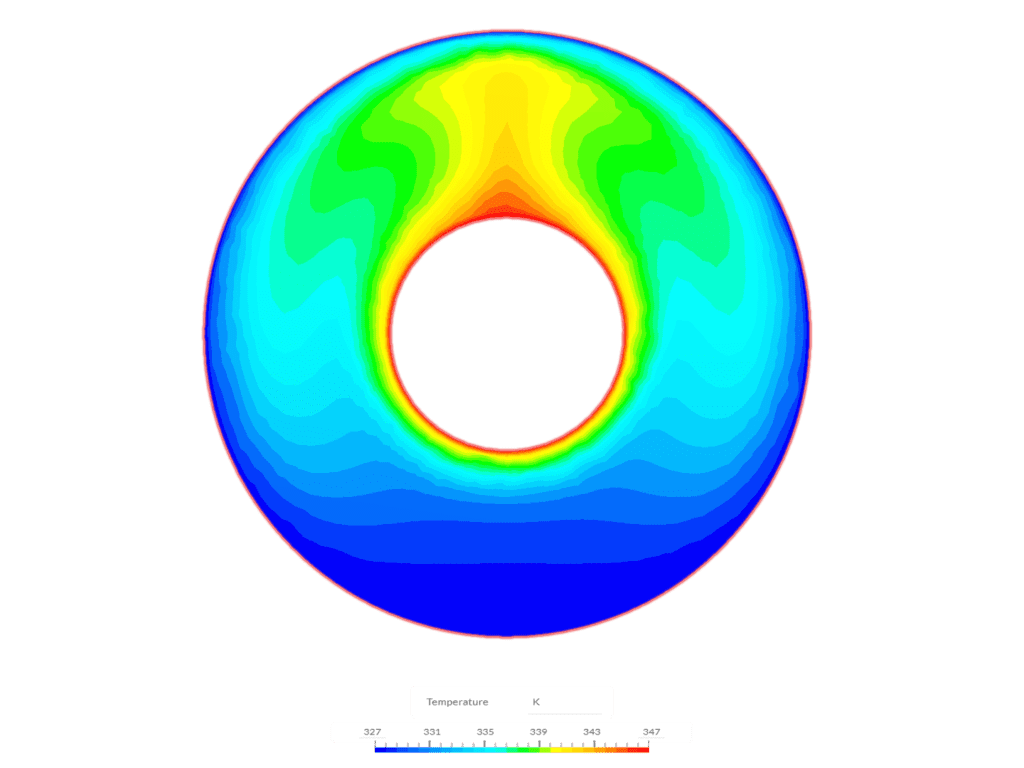
A good agreement is found between the results of the Convective Heat Transfer solver and the results reported in the experimental work for the convection between the concentric cylinders. The temperature distribution in the cross-section of the air volume can be visualized in Figure 5:

Last updated: December 28th, 2022