Validation Case: Conjugate Heat Transfer – Rectangular Fins

This validation case belongs to fluid dynamics. The aim of this validation case is to validate the Conjugate heat transfer (CHT) v2.0 analysis implemented in SimScale.

The simulation results of SimScale were compared to the results presented in the study titled “Unshrouded Plate Fin Heat Sinks for Electronics Cooling: Validation of a Comprehensive Thermal Model and Cost Optimization in Semi-Active Configuration”$^1$ written by L. Ventola, G. Curcuruto, et. al.

View Project

Geometry

The geometry used for the case has three regions, which are as follows:

1. Enclosure – Fluid Region

The length of the fluid region upstream of the heat sink is 6 times the length of the heat sink $(L)$ and the fluid region length downstream is 15 times $L$ visualized in the figure below:

Validation Heat Sink Windtunnel Dimensions — Figure 1: Dimension of enclosure based on the length of the heat sink

2. Heat Sink

The model of the heat sink with its dimensions can be seen in the figure and table below:

model of heat sink used for conjugate heat transfer validation case — Figure 2: Heat sink model

Dimension $[mm]$	Value
h (height)	21.8
W (width)	41.4
L (length)	57.2
t_b (base height)	8.4
t (thickness of fin)	1
p (spacing between adjacent fins)	2.1
N (number of fins)	14

Table 1: Dimensions of the heat sink

3. Heat Source

The heat source is a chip with the dimensions shown in the table below and has a contact surface area $(A_s)$ with a heat sink of 1.555 $cm^2$.

Validation Heat Sink Chip Dimensions — Figure 3: Chip heat source used in validation case

Dimension $[mm]$	Value
a	15.5
b	10
c	4.5
d	9
e	1.3

Table 2: Chip dimension in $mm$

Chip Model

STP130NS04ZB by STMicroelectronics

Analysis Type and Mesh

Tool Type: OpenFOAM®

Analysis Type: Conjugate Heat Transfer v2.0

Mesh and Element Types:

The mesh was generated using the Standard meshing algorithm. The following table provides the details of the mesh:

Mesh Type	Number of Cells	Element Type
Standard	0.92 million	3D Tetrahedral/Hexahedral

Table 3: Details of the generated mesh

Validation Heat Sink Windtunnel Mesh — Figure 4: Standard mesh of enclosure with outer tetrahedral cells and hex core

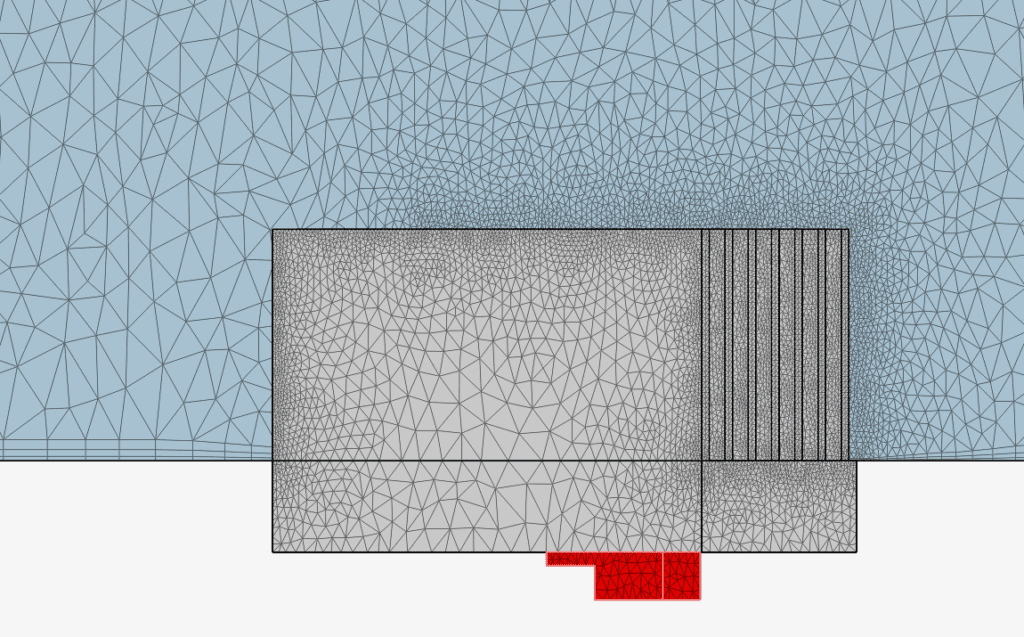
A region refinement was added to the heat source, heat sink, and the area close to the heat sink to be able to accurately capture the features of the heat sink as well as the wake region. In order to reduce the cell count and therefore decrease the run time, a symmetry plane in the XZ-Plane is used. A local element refinement was further used to increase the fineness around the fins of the heat sink. The mesh of the heat sink, heat source, and symmetry plane can be seen in the figure below:

Validation Heat Sink Chip Heat Sink Mesh — Figure 5: Mesh of the heat sink and heat source with local element refinement with a maximum edge length of 0.001 $m$ and the mesh on the symmetry plane

Simulation Setup

Material:

Fluid:
- Air
  - Kinematic viscosity $(\nu)$: 1.529e-5 $m^2/s$
  - Density $(\rho)$: 1.179 $kg/m^3$
  - Thermal expansion coefficient: 3.43e-3 $1/K$
  - Reference temperature $(T_0)$: 273.1 $K$
  - Laminar Prandtl number $(Pr_{lam})$: 0.713
  - Turbulent Prandtl number $(Pr_{turb})$: 0.85
  - Specific heat: 1013 $J/(kg\ K)$
Solid:
- Heat sink – Aluminium:
  - Thermal conductivity $(\kappa)$: 209 $W/(m\ K)$
  - Specific heat: 897 $J/(kg\ K)$
  - Density $(\rho)$: 2700 $kg/m^3$
- Power Source:
  - Thermal conductivity $(\kappa)$: 38.6 $W/(m\ K)$
  - Specific heat: 705 $J/(kg\ K)$
  - Density $(\rho)$: 2330 $kg/m^3$
- Thermal resistance between the heat sink and power source $(R_{jc})$) is 0.5 $K/W$.
- Since the material properties of the heat source were not provided, the conductivity of the heat source was calculated to be 38.6 $K/W$ with the following formula:

$$\kappa_{hs} = \frac{\frac{1}{2}a}{R_{jc}A_s} \tag{1}$$

where:

$\kappa_{hs}$: conductivity
$a$: side length of heat source
$R_{jc}$: junction-to-air resistance
$A_s$: contact surface area

Initial Conditions:

The velocity $(U)$ and temperature $(T)$ are given an initial condition, based on the experimental results, the same as for the boundary conditions to allow for faster convergence of the simulation.

Boundary Conditions:

Surface	Boundary Condition
1	Volumetric Flow Inlet
2	Pressure Outlet
3	Symmetry Plane
4	Symmetry Plane Heat Sink
5	Symmetry Plane Chip

Table 4: Boundary Condition for individual surfaces

The simulation was run with 7 different volumetric flow rates with each volumetric flow rate having its corresponding inlet temperature and heat source, as seen in the table below:

$\dot{U}\,[m^3/s]$	$T\,[K]$	Heat Flux $[W]$	Pressure Outlet $[Pa]$	Walls	Heat Sink
0.0547	296.9	56.64	0	No-slip	No-slip
0.0703	297.4	71.4	0	No-slip	No-slip
0.0859	297.9	82.36	0	No-slip	No-slip
0.0996	298.3	87.32	0	No-slip	No-slip
0.1123	298.9	85.07	0	No-slip	No-slip
0.1250	299.3	76.3	0	No-slip	No-slip
0.1357	299.6	60.24	0	No-slip	No-slip

Table 5: Inlet volumetric flow rate with its corresponding inlet temperature

Note

The walls of the heat sink were automatically assigned as walls with temperature as zero gradient. This assignment cannot be seen under Boundary conditions in the attached project.

Reference Solution

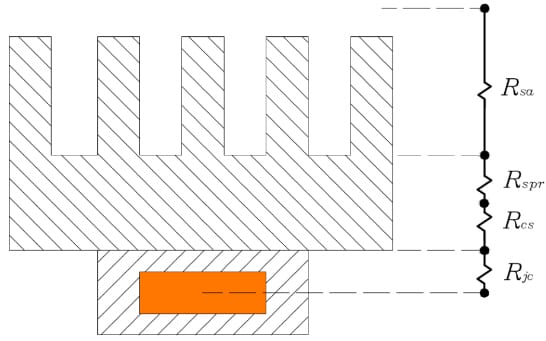
The overall heat resistance between the heat source and the ambient air (heat sink) $(R_{ja})$ as calculated in the analytical and experimental results from the reference study$^1$ are explained as follows. The complete array of thermal resistances between the heat source and the ambient air can be seen in the figure below:

conjugate heat transfer validation thermal resistances between the heat source and the ambient air — Figure 7: Illustration of thermal resistances between the heat source and the ambient air (Ventola, et.al. 2016)$^1$

1. Analytical

The analytical solution for the junction-to-air thermal resistance is given by:

$$R_{ja,t} = R_{jc}+R_{cs}+R_{sa}+R_{spr} \tag{2}$$

where:

$R_{ja,t}$: analytical junction-to-air thermal resistance
$R_{jc}$: junction-to-case thermal resistance
$R_{cs}$: case-to-sink thermal resistance
$R_{sa}$: sink-to-air thermal resistance
$R_{spr}$: spreading thermal resistance

2. Experimental

The experimental solution is gained by doing an experiment with the scheme explained in the figure below:

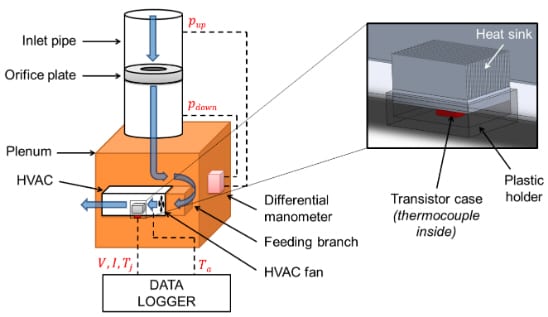
conjugate heat transfer validation experimental setup of measuring junction to air thermal resistance — Figure 8: Experimental setup of heat sink thermal model validation (Source: Ventola, et.al, 2016)$^1$

The air at ambient temperature flows into the rig and the airflow is measured with an orifice plate method where the orifice plate is in the inlet pipe. Then, the air flows into a plenum chamber and finally passes through a feeding branch, and enters the HVAC. The HVAC fan flows the air through the experimental rig where the heat sink is placed.

The transistor voltage drop ($V$), electric current ($I$), junction temperature ($T_j$) and the temperature of air approaching the heat sink ($T_a$) are measured with a GL220 data logger (Graphtec™ Digital Solutions, Plano, TX, USA)$^1$. The junction temperature ($T_j$) is measured at the interface between the transistor and the heat sink and the approaching air temperature ($T_a$) is measured at the inlet of the HVAC. Finally, the overall junction-to-air thermal resistance is calculated with the formula below:

$$R_{ja,e} = \frac{T_j-T_a}{P} \tag{3}$$

Where:

$R_{ja,e}$: thermal resistance between the heat source and the heat sink from experimental results
$T_j$: measured junction temperature
$T_a$: ambient temperature
$P$: thermal power of the heat source

Result Comparison

The junction-to-air thermal resistance ($R_{ja}$) obtained from SimScale was calculated with the formulae below:

$$T_{j,s} = T_{interface} + P.R_{jc} \tag{4}$$

$$R_{ja,s} = \frac{T_{j,s}-T_a}{P} \tag{5}$$

Where:

$T_{j,s}$: junction temperature of simulation
$T_{interface}$: the temperature at the interface of the heat source and the heat sink
$P$: thermal power of the heat source
$R_{j,c}$: thermal resistance between the heat source and the heat sink
$R_{ja,s}$: junction-to-air thermal resistance obtained from simulation
$T_a$: ambient temperature

The comparison of the junction-to-air thermal resistance ($R_{ja}$) between the simulation results and the results in the reference study is given in Table 5 and Figure 9:

$\dot{U}\,[m^3/s]$	$T_a$ $[K]$	P $[W]$	$T_{j,e}$ $[K]$	$R_{ja,t}$ $[K/W]$	$R_{ja,e}$ $[K/W]$	$T_{j,s}$ $[K]$	$R_{ja,s}$ $[K/W]$	Error – Simulation to Analytical [%]	Error – Simulation to Experiment [%]
0.0547	296.95	56.64	371.25	1.203	1.312	370.91	1.230	8.55	-0.47
0.0703	297.35	71.4	384.15	1.142	1.216	384.64	1.145	7.05	-0.47
0.0859	297.95	82.36	391.85	1.1	1.140	394.00	1.071	6.03	2.30
0.0996	298.25	97.32	395.05	1.071	1.109	407.75	1.085	5.06	1.46
0.1123	298.95	85.07	391.15	1.05	1.084	391.92	1.073	4.09	0.82
0.1250	299.25	76.3	377.45	1.031	1.024	380.76	1.054	3.61	4.32
0.1357	299.65	60.24	357.55	1.017	0.961	362.75	1.040	3.00	9.00

Table 6: Comparison of results between analytical, experimental, and simulation

conjugate heat transfer validation Heat Sink Thermal Resistance [K_W] — Figure 9: Graphical visualization of results between the analytical, experiment, and simulation.

The temperature distribution on the heat sink and chip obtained from the simulation when the velocity is 14 $m/s$ is as below:

conjugate heat transfer validation Heat Sink Velocity Temperature VDot0_1357 — Figure 10: Temperature distribution of power source and heat sink and Velocity distribution.

References

Ventola, L., Curcuruto, G., Fasano, M., Fotia, S., Pugliese, V., Chiavazzo, E. and Asinari, P., Unshrouded Plate Fin Heat Sinks for Electronics Cooling: Validation of a Comprehensive Thermal Model and Cost Optimization in Semi-Active Configuration, Energies 8 (9), 2016, DOI:10.3390/en9080609