Rotating Motion

The rotating motion boundary condition is used to define a rigid body rotation of the assigned entities. The user can define the rotation axis, the base point, and the rotation angle. Each component can be defined with a formula or table input.

This boundary condition is only available for static, dynamic, and thermomechanical analysis types. Find below its formulation and the required inputs.

If \(\mathbf{R}_{\theta}^{a}\) denotes the rotation matrix of a general rotation about the axis \(a\) with an angle of \(\theta\), then the displacement \(\vec u\) of a point \(\vec X\) is calculated as:

$$\vec{u} = \mathbf{R}_{\theta}^{a} \cdot (\vec{X}- \vec{P}_0) + \vec{P} -\vec{X}$$

where \(\vec P\)  denotes the axis base point and \(\vec {P}_0\) is the position at time \(t = 0\).

Base Point

This point is the base point for the rotation axis. A possible movement of the base point regarding the initial position at time \(t = 0\) during the rotation process is taken into account.

Rotation Axis

The rotation axis is defined by its three components in the global coordinate system. The right-hand rule applies, to determine the direction of the rotation.

Rotation Angle

The rotation angle is defined in a mathematical positive sense around the rotation axis. The input can be in \(rad\) or degrees.

Example

In the example below, a unit cube is rotated around the z-axis. The base point is moving in positive z-direction at 1 \(m/s\).

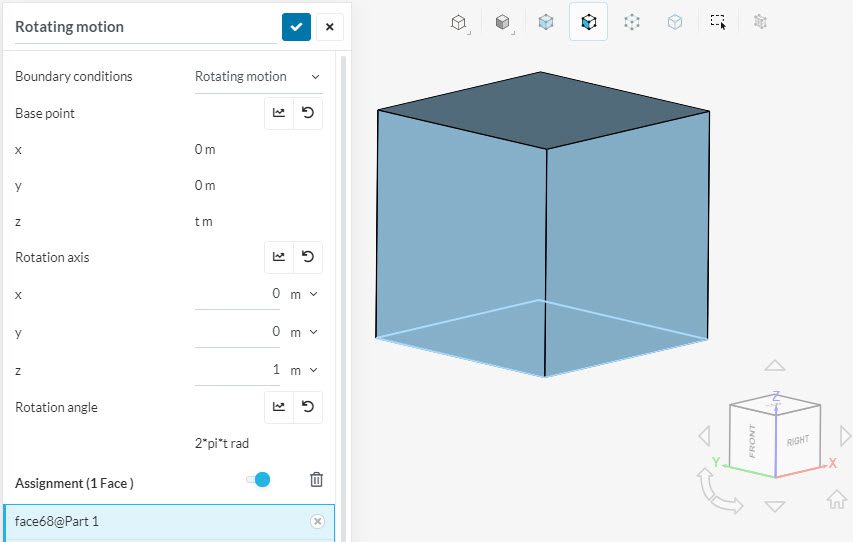
The bottom face was assigned and the corresponding settings were:

• Base Point: \((0, 0, t)\). This causes the cube to translate in the positive z-direction, at 1 \(m/s\);
• Rotation axis: \((0, 0, 1)\); 
• Rotation angle: \(2.\pi.t\), representing a continuous rotating velocity of 60 rotations per minute around the z-axis.

The video below shows the result of a simulation with the described boundary condition:

Last updated: July 13th, 2023