websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationAnalysis TypesPedestrian Wind Comfort AnalysisPedestrian Comfort MapWind Comfort Evaluation Based on Gust Equivalent Mean

    Wind Comfort Evaluation Based on Gust Equivalent Mean

    When studying pedestrian wind comfort, the typical approach is to use the mean wind velocity for the comfort calculations. When reporting a wind comfort study, some authorities may require to take the Gust Equivalent Mean (GEM) into account.

    Wind gusts often represent additional discomfort to the pedestrians when compared to the mean wind velocity. In this sense, the gust equivalent mean formulation is a way to account for sudden wind accelerations, which are common in external aerodynamics. For this reason, considering the GEM for pedestrian comfort studies is valuable.

    As far as simulation setup goes, there are no additional steps required to obtain wind comfort results based on GEM. The data is available for all new Pacefish®\(^1\) Pedestrian Wind Comfort (PWC) simulations by default. The image below shows the available options in the post-processing environment:

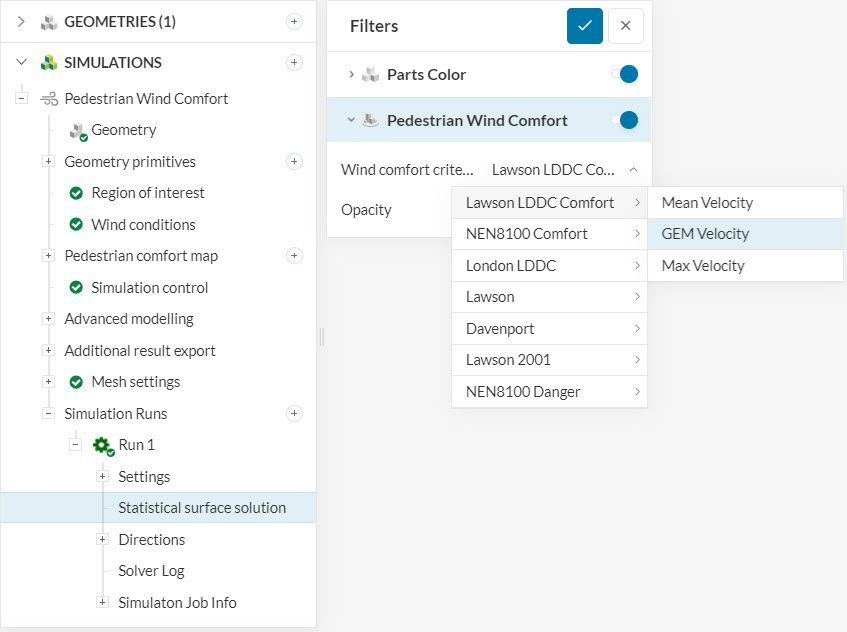
    inspecting gust equivalent mean pwc results GEM
    Figure 1: Selecting GEM data for the wind comfort criteria in the Statistical surface solution of a PWC study.

    Find below more details on the gust equivalent mean implementation in the SimScale platform.

    Gust Equivalent Mean Formulation

    Before calculating the gust equivalent mean speed \(U_{GEM}\), first it’s necessary to understand the concept of gust speed \(U_{gust}\). In the literature\(^2\), the gust speed is taken as the highest sustained gust over a 3-second period.

    To evaluate the gust speed in a certain region of the domain, it is common practice to apply statistical methods. SimScale uses the following formulation:

    $$ U_{gust} = U_{mean}+k_{g}\sigma \tag{1} $$

    Where \(U_{mean}\) is the mean velocity, \(k_{g}\) is the gust factor and is equal to 3.5 \(^3\), and \(\sigma\) is the standard deviation of velocity.

    Since PWC simulations use the DDES turbulence model, the turbulence has two components, resolved and modeled. The total standard deviation \(\sigma\) takes into account:

    • \(\sigma_{DDES}\), the standard deviation of the velocity fluctuations, and
    • \(\sigma_k\), the standard deviation from the modeled turbulence kinetic energy \(k\)
      \(\sigma_k = \sqrt{\frac{2k}{3}}\).

    Thus, the total standard deviation is given by

    $$ \sigma = \sqrt{(\sigma_{DDES})^2 + (\sigma_k)^2} = \sqrt{(\sigma_{DDES})^2 + \frac{2k}{3}} \tag {2} $$

    At last, equation 3 below correlates \(U_{GEM}\) and \(U_{gust}\):

    $$ U_{GEM} = \frac{U_{gust}}{1.85} \tag {3} $$

    Post-Processing

    Based on Figure 1, the comfort criteria results are available in SimScale under three categories:

    1. The Mean Velocity uses exclusively the mean velocity data.
    2. The GEM Velocity only takes the GEM values into account.
    3. Finally, for Max Velocity, the platform uses the maximum velocity between mean and GEM to plot the comfort map. Therefore, this approach is the most conservative.

    Find below a comparison between the comfort criteria on the rooftop of two buildings using different velocity configurations:

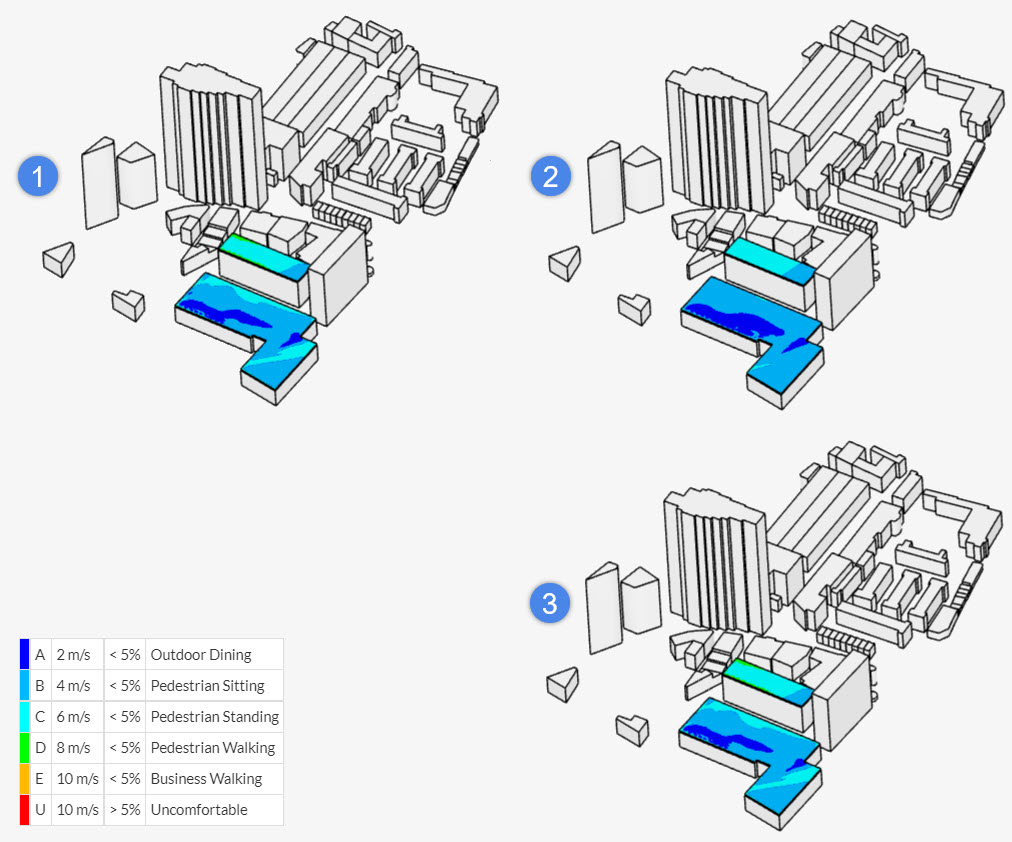
    simscale pedestrian comfort results gem
    Figure 2: Pedestrian comfort maps using mean velocity (1), GEM velocity (2), and max velocity (3) for the Lawson LDDC Comfort criteria.

    In the case above, the mean velocities are larger than the GEM on the rooftops, leading to configuration 1 showing less comfort than configuration 2. Naturally, the max velocity configuration shows the worst scenario, by taking the maximum velocities between mean and GEM.

    References

    Last updated: January 5th, 2024

    Contents