Error: Time Step Below Threshold

What Happened?

The solution didn’t achieve Newton convergence at some point and the automatic time-stepping computed a time step value that is lower than the minimum allowed by the user.

What Could Be the Possible Reason?

The setup for automatic time-step computation is incoherent.

What Can I Do Now?

As this error is related and revealed due to lack of Newton convergence, the first advice is to try and solve that error. Please refer to the specific documentation for that error: Newton Convergence could not be Reached.

If the error persists after applying the suggestions there, it might be the case that the simulation actually needs small time steps to compute the solution. This can happen in cases with high non-linearities or fast dynamics.

In that case, go to the Simulation Control panel:

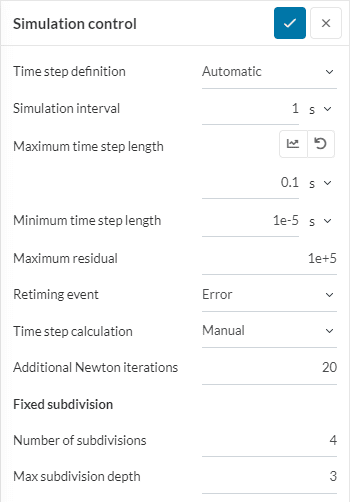
Here we can find the default values for the relevant parameters of the Automatic time-step definition algorithm:

• Time-step definition: Automatic
• Maximum (initial) time step length \(\Delta t_{max} = \) 0.1 \(s\)
• Minimum time step length \(\Delta t_{min} = \) 1e-5 \(s\)
• Time-step calculation: Manual
• Number of subdivisions \(n = \) 4
• Max subidivision depth \(m = \) 3

The algorithm works by sub-dividing the time step into \(n\) equal parts, in the event of an error due to divergence of the solution during the integration process. If further errors occur, it then applies the subdivision rule again, until the time step falls below the minimum. In this sense, we can see that the time step after \(i\) subdivisions is given by the formula:

$$ \Delta t_i = \frac{ \Delta t_{max} }{ n ^ i } $$

Then it follows that at the last subdivision given by \( i = m \), the time step is:

$$ \Delta t_{ i = m } = \frac{ \Delta t_{max} }{ n ^ m } $$

Which should always be larger than the minimum time step to avoid the occurrence of the error. This gives us the rule to select the minimum time step length:

$$ \Delta t_{min} \leq \frac{ \Delta t_{max} }{ n ^ m } $$

In the case of the default values:

$$ 1×10^{-5} \leq \frac{0.1}{4^3} = 1.5625×10^{-3} $$