This validation case belongs to pressure load in solid mechanics. The aim of this test case is to validate the following parameters:
The simulation results of SimScale were compared to the numerical results presented in [NAFEMS]\(^1\).
The geometry used for the case is as follows:
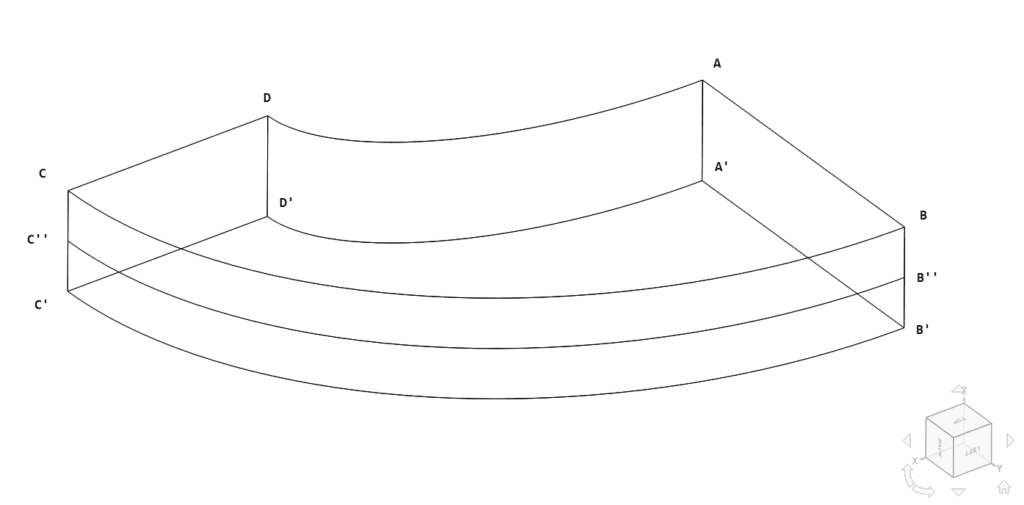
The plate has a thickness of 0.6 \(m\). Table 1 presents the coordinates for each point:
| Point | X [\(m\)] | Y [\(m\)] | Z [\(m\)] |
|---|---|---|---|
| A | 0 | 1 | 0.6 |
| B | 0 | 2.75 | 0.6 |
| C | 3.25 | 0 | 0.6 |
| D | 2 | 0 | 0.6 |
| A’ | 0 | 1 | 0 |
| B’ | 0 | 2.75 | 0 |
| C’ | 3.25 | 0 | 0 |
| D’ | 2 | 0 | 0 |
The point B” is located at the middle of edge BB’ while point C” is located at the middle of edge CC’. The curves of edges BC and AD are defined by equations 1 and 2 respectively:
$$ ( \frac{x}{3.25} )^2 + ( \frac{y}{2.75} )^2 = 1 \tag{1} $$
$$ ( \frac{x}{2} )^2 + y^2 = 1 \tag{2} $$
Tool Type: Code_Aster
Analysis Type: Static Linear
Mesh and Element Types:
All meshes were computed locally and uploaded to the platform. Table 2 presents the details of the meshes used for each case:
| Case | Mesh Type | Number of Nodes | Element Type |
|---|---|---|---|
| A | 1st Order Tetrahedral | 26639 | Standard |
| B | 2nd Order Tetrahedral | 194237 | Standard |
| C | 1st Order Hexahedral | 36 | Standard |
| D | 2nd Order Hexahedral | 111 | Standard |
| E | 1st Order Hexahedral | 105 | Standard |
| F | 2nd Order Hexahedral | 349 | Standard |
| G | 2nd Order Hexahedral | 52941 | Standard |
Material:
Boundary Conditions:
The reference solution as presented in [NAFEMS]\(^1\) is of the numerical type. For the comparison purposes, the normal stress at point D in the direction of the Y axis is taken:
\( \sigma_{ref} = 5.38\ MPa \)
Comparison of stress \(\sigma_{yy}\) magnitude computed at the location of point D (variable SIYY) from the simulation results is presented with respect to the reference solution \(\sigma_{ref}\):
| CASE | \( \sigma_{ref} \) [MPa] | \( \sigma_{YY} \) [MPa] | Error |
|---|---|---|---|
| A | 5.38 | 5.16166 | -4.06 % |
| B | 5.38 | 5.40075 | 0.39 % |
| C | 5.38 | 3.98345 | -25.96 % |
| D | 5.38 | 5.47091 | 1.69 % |
| E | 5.38 | 5.10811 | -5.05 % |
| F | 5.38 | 5.71058 | 6.14 % |
| G | 5.38 | 5.38599 | 0.11 % |
The von Mises stress color plot is presented for the results of case G:
References
Note
If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.
Last updated: July 15th, 2020
We appreciate and value your feedback.
