Documentation
This thermal stress analysis of a polymeric photo-thermal microactuator validation case belongs to thermomechanics. This test case aims to validate the following:
The simulation results of SimScale were compared to the analytical results presented in [Elbuken et al.]\(^1\).
A total of 13 microactuator geometries are evaluated in this validation case. The base geometry is shown below:
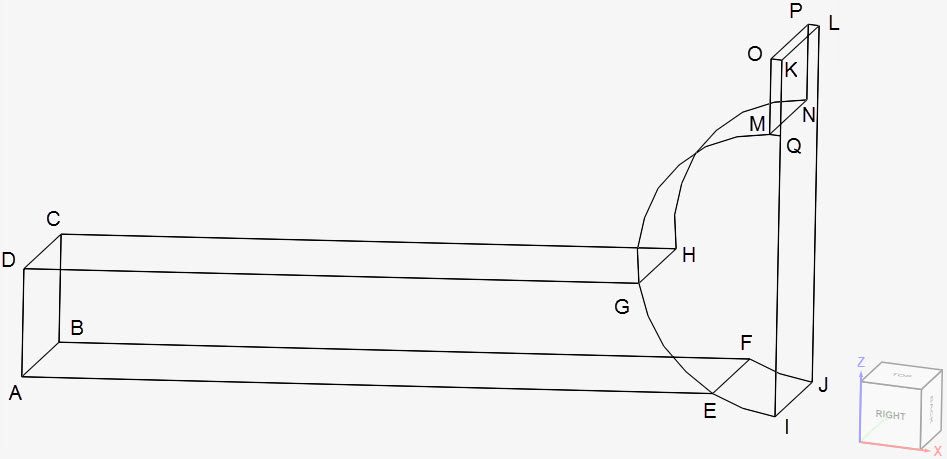
The 13 geometries are divided into two groups. Using Figure 2 as a reference, for the group A geometries, the length L and width W of the microactuator remains constant, whereas the bending angle \(\theta\) varies.
For group B, the length L and bending angle \(\theta\) are constant, and the width W changes. For all geometries, the radius R and thickness of the microactuator, in the y-direction, remains constant. Due to symmetry, only half of the model was taken for the analysis.
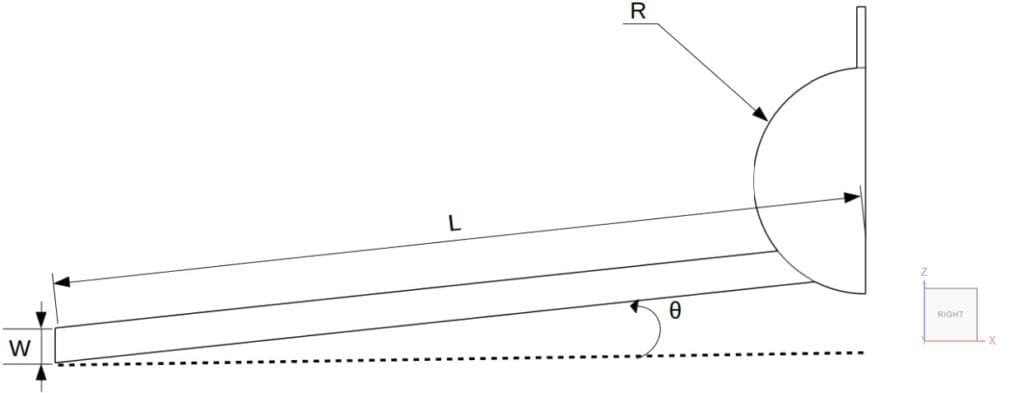
Table 1 provides an overview of the dimensions:
| Case | R \([\mu m]\) | Thickness in y-direction \([\mu m]\) | W \([\mu m]\) | L \([\mu m]\) | \(\theta\) [º] |
| A1 | 130 | 100 | 50 | 1000 | 6 |
| A2 | 130 | 100 | 50 | 1000 | 8 |
| A3 | 130 | 100 | 50 | 1000 | 10 |
| A4 | 130 | 100 | 50 | 1000 | 12 |
| A5 | 130 | 100 | 50 | 1000 | 14 |
| B1 | 130 | 100 | 30 | 700 | 6 |
| B2 | 130 | 100 | 40 | 700 | 6 |
| B3 | 130 | 100 | 50 | 700 | 6 |
| B4 | 130 | 100 | 60 | 700 | 6 |
| B5 | 130 | 100 | 70 | 700 | 6 |
| B6 | 130 | 100 | 80 | 700 | 6 |
| B7 | 130 | 100 | 90 | 700 | 6 |
| B8 | 130 | 100 | 100 | 700 | 6 |
Tool Type: Code Aster
Analysis Type: Thermomechanical analysis type
Mesh and Element Types: All meshes were created with the standard algorithm, using second-order elements. Table 2 presents a summary of the meshes:
| Case | Mesh Type | Nodes | Element Type |
| A1 | 2nd-order standard | 194853 | Standard |
| A2 | 2nd-order standard | 479747 | Standard |
| A3 | 2nd-order standard | 360734 | Standard |
| A4 | 2nd-order standard | 466753 | Standard |
| A5 | 2nd-order standard | 257295 | Standard |
| B1 | 2nd-order standard | 102941 | Standard |
| B2 | 2nd-order standard | 134074 | Standard |
| B3 | 2nd-order standard | 130987 | Standard |
| B4 | 2nd-order standard | 132192 | Standard |
| B5 | 2nd-order standard | 142016 | Standard |
| B6 | 2nd-order standard | 152533 | Standard |
| B7 | 2nd-order standard | 165596 | Standard |
| B8 | 2nd-order standard | 173364 | Standard |
Find below the mesh used for case B8. It’s a standard mesh with second-order tetrahedral cells.
Material:
Boundary Conditions:
The analytical solution is given by the equations presented in [Elbuken et al.]\(^1\).
Find below the comparison between the analytical solution and SimScale results. The quantity measured is the displacement of the tip of the structure (face OPLK).
The first plot shows the results for cases A1 through A5:
Similarly, for cases B1 through B8, Figure 5 shows the result comparison:
In Figure 6, we can see the displacement contours for case B8:
Last updated: November 7th, 2023
We appreciate and value your feedback.
Sign up for SimScale
and start simulating now