websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Thermal Bridge Case 1 – Half Square Column

    Validation Case: Thermal Bridge Case 1 – Half Square Column

    This validation case belongs to heat transfer, with the case of a half square column subjected to the imposed temperature gradient. The aim of this project is to demonstrate the validity of SimScale’s Heat Transfer solver by replicating the standard test case and comparing the following parameters:

    • Temperature distribution

    The simulation results from SimScale were compared to the reference results presented in the standard EN-ISO 10211, validation case 1 (Annex C)\(^1\).

    View Project

    Geometry

    The half square column is illustrated in Figure 1:

    half square column heat transfer simscale
    Figure 1: Model geometry, with half of the square column being considered for the analysis.

    The column has dimensions of 2 x 1 x 0.1 \(m\), forming a half-square.

    Analysis Type and Mesh

    Tool Type: Code_Aster

    Analysis Type: Heat Transfer

    Mesh and Element Types:

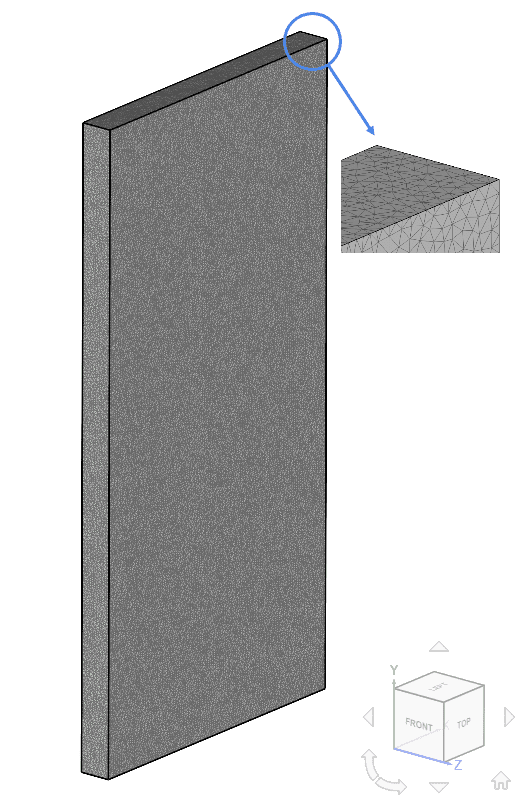
    The mesh was computed using SimScale’s Standard meshing algorithm, with the fineness parameter maxed up to 10. Statistics of the resulting mesh are presented in Table 1, and illustration shown in Figure 2:

    Mesh #Mesh TypeElement TypeNumber of NodesNumber of Elements
    1Standard1st order tetrahedrals2733451431857
    Table 1: Finite elements mesh details
    mesh heat transfer simscale
    Figure 2: Finite elements tetrahedral mesh used for the thermal simulation using SimScale’s Standard meshing algorithm.

    Simulation Setup

    Material:

    • \((\rho)\) Density: 1 \(kg/m^3\)
    • Conductivity: Isotropic
    • \( (\kappa)\) Thermal conductivity: 1 \( W/(m.K) \)
    • Specific Heat: 1 \( J/(kg.K) \)

    Boundary Conditions:

    • Fixed Temperatures:
      • Top wall: 20 \(°C\)
      • External wall: 0 \(°C\)
      • Bottom wall: 0 \(°C\)
    • Adiabatic:
      • Front and back walls
      • Symmetry face
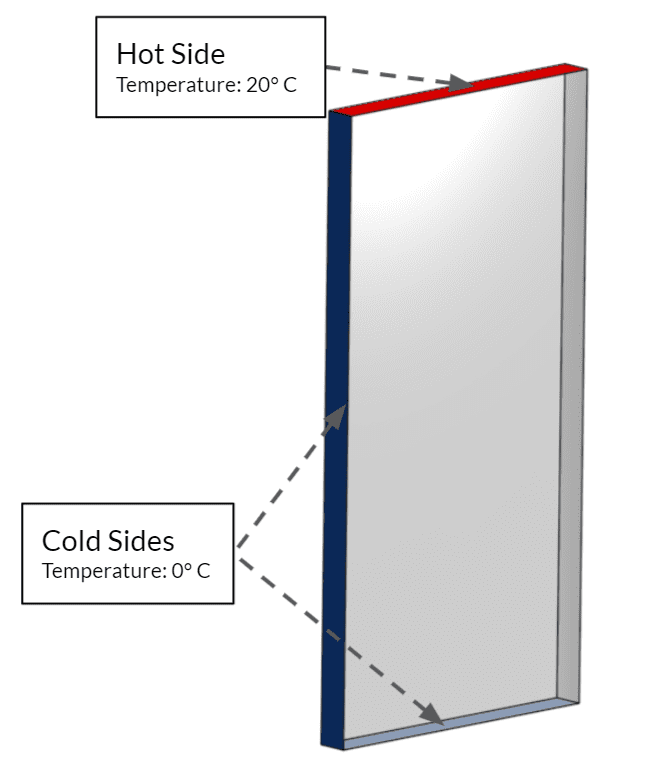
    boundary conditions heat transfer simscale
    Figure 3: Illustration of the boundary conditions. The unassigned faces (front, back and symmetry) automatically get treated as adiabatic walls.

    Reference Solution

    The reference solution for the half square column is of the analytical type. It is presented as the computed temperatures in \(°C\) at a set of points located in a 7×4 equidistant grid across the column (28 points). The reference values are presented in Table 2:

    Row/Column1234
    19.713.414.715.1
    25.38.610.310.8
    33.25.67.07.5
    42.03.64.75.0
    51.32.33.03.2
    60.71.41.81.9
    70.30.60.80.9
    Table 2: Grid point temperatures values in \(°C\) across the half square column from the reference\(^1\)
    probe points heat transfer simscale
    Figure 4: Point locations for temperature values comparison. Rows are numbered top to bottom and columns left to right.

    Results Comparison

    The computed temperature values in SimScale are presented in Table 3:

    Row/Column1234
    19.713.414.715.1
    25.38.610.310.8
    33.25.67.07.5
    42.03.64.75.0
    51.32.33.03.2
    60.71.41.81.9
    70.30.60.80.9
    Table 3: Grid points temperatures values in \(°C\) across the half square column as obtained using SimScale

    Results show that, up to one decimal place of precision, the values computed by SimScale match the theoretical values presented in the standard. The acceptance criterion states that the difference between the computed temperatures by the method being validated and the listed temperatures shall not exceed 0.1\(°C\). Thus, it is found that the SimScale solver is accepted under the standard’s validation case 1.

    half square column temperature plot heat transfer simscale
    Figure 5: Temperature contours in the half square column, showing gradient from hot to cold regions

    References

    Note

    If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.

    Last updated: June 14th, 2021

    Contents