Validation Case: Solar Load on an Airbox

This solar load validation case belongs to fluid dynamics and heat transfer including solar radiation. This test case aims to validate the solar load model on a small airbox. The results obtained from the simulation were compared to the analytical solution. The parameter that was compared is:

• Surface temperature of the plate

Geometry

The geometry of the airbox has the following dimensions:

• Height: 0.005 \(m\)
• Width: 0.15 \(m\)
• Length: 0.15 \(m\)

The top surface has a fixed temperature and the side walls are set adiabatically. The bottom surface is the wall for which the temperature is to be calculated and compared. The solar load is applied in the normal direction of the wall.

Analysis Type and Mesh

Tool type: OpenFOAM

Analysis type: Incompressible Conjugate Heat Transfer with radiation

Turbulence model: \(k-\omega\) SST turbulence model

Time dependency: Steady-state

Mesh and element types: The mesh was created using SimScale’s standard mesher. The box has 13,000 cells and a boundary layer mesh on the wall surface.

Simulation Setup

Material:

• Air
  • Kinematic viscosity \(\nu\) = 1.529e-5 \(\frac{m^2}{s}\)

Boundary conditions:

Top and side surfaces:

• Top surface: Constant Temperature 300 \(K\)
• Side walls: Adiabatic

Wall without thermal wall modeling:

• Wall Model: External Wall Heat Flux Heat transfer coefficient: 10 \( \frac{W}{Km^2}\)
  • Ambient Temperature: 330 \(K\)
  • Wall thermal: No Wall Thermal
  • Outer surface emissivity: 0.9
  • Solar radiative behavior: Opaque
  • Emissivity: 0.9

Wall with thermal wall modeling:

• Wall Model: External Wall Heat Flux
  • Heat transfer coefficient: 10 \( \frac{W}{Km^2}\)
  • Ambient Temperature: 330 \(K\)
  • Wall thermal: Layer Wall thermal
  • Thermal conductivity: 0.3 \(\frac{W}{m K}\)
  • Layer thickness: 1 \(m\)
  • Outer surface emissivity: 0.9
  • Solar radiative behavior: Opaque
  • Emissivity: 0.9

Side Walls: Adiabatic

Reference Solution

For the validation of the solar load, the analytical solution for the wall temperature was calculated using the following equations\(^1\):

Temperature Calculation Without Thermal Wall Modeling

Equations for heat flux from ambient to wall and heat flux from wall to top:

$$ q_{Ambient To Wall} = (T_{Wall}-T_{A}) * h \ – q_{SolarDiff} * \epsilon \tag{1}$$

$$ q_{Wall To Top} = (T_{T}-T_{Wall}) * {\frac{\kappa_f}{h_f}} + q_{SolarDir} * \epsilon \tag{2}$$

Continuity of heat flux:

$$ q_{Ambient To Wall} = q_{Wall To Top} \tag{3} $$

Put equation 1 and 2 into equation 3 and solve for \(T_{Wall}\)

$$ T_{Wall} = \frac{1}{h + \frac{\kappa_f}{h_{f}}} \left( T_{T} * \frac{\kappa_f}{h_{f}} + T_{A} * h + (q_{SolarDiff} + q_{SolarDir}) * \epsilon \right)\tag{4} $$

Where,

• \(T_{Wall}\) : Wall Temperature \(K\)
• \(T_{A}\): Ambient Temperature \(K\)
• \(T_{T}\): Top Temperature \(K\)
• \(h\): Heat transfer coefficient wall \(\frac{W}{Km^2}\)
• \(q_{SolarDiff}\): Diffuse solar load \(\frac{W}{m^2}\)
• \(q_{SolarDir}\): Direct solar load \(\frac{W}{m^2}\)
• \(\epsilon\): Emissivity
• \(\kappa_f\): Thermal conductivity of the fluid \(\frac{W}{Km}\)
• \(h_{f}\): Height of fluid \(m\)

Temperature Calculation With Thermal Wall Modeling

For the validation of the solar load, the analytical solution for the wall temperature was calculated using the following equations:

$$ q_{Ambient To Wall} = (T_{Th}-T_{A})*h- q_{SolarDiff}*\epsilon \tag{5} $$

$$ q_{Wall To Top} = (T_{T}-T_{Wall})*\frac{\kappa_f}{h_f} + q_{SolarDir}*\epsilon \tag{6} $$

Calculation of the thermal wall temperature:

$$ T_{Th} = T_{Wall}*(1-\lambda)+\lambda*T_{A} +q_{SolarDiff}*\frac{\epsilon}{h+\frac{\kappa_{tw}}{h_{tw}}} \tag{7}$$

Calculation of \(\lambda\) from the setup of the thermal wall:

$$\lambda = \frac{h}{h+\frac{\kappa_{tw}}{h_{tw}}}\tag{8}$$

Continuity of heat flux:

$$q_{Ambient To Wall} = q_{Wall To Top} \tag{9}$$

Equation 5, 6, 7, 8 into Equation 9 and solving for \(T_{Wall}\)

$$ T_{Wall} =\frac{1}{(1-\lambda)*h+\frac{\kappa_f}{h_f}} \left(-h * \left( (\lambda -1) * T_{A} + q_{SolarDiff} * \frac{\epsilon}{h+\frac{\kappa_{tw}} {h_{tw}}}\right) + T_{T} * \frac{\kappa_f}{h_f}+\epsilon * \left( q_{SolarDiff}+ q_{SolarDir}\right) \right) \tag{10}$$

Where,

• \(T_{Th}\) : Temperature of thermal wall \(K\)
• \(\kappa_{tw}\): Thermal conductivity of the thermal wall \(\frac{W}{Km}\)
• \(h_{tw}\): Height of thermal wall \(m\)

Results

Comparison of the analytical results to the results obtained from SimScale simulation for the surface temperature:

Case	Analytical Result \([K]\)	Simulation Result \([K]\)	Deviation \( [\%] \)
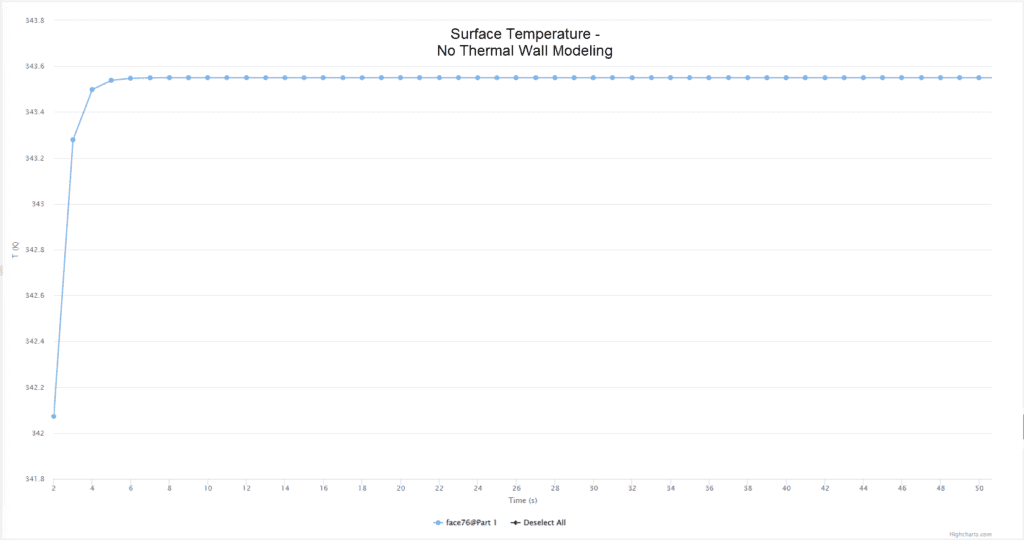
No thermal Wall Modeling	343.3	343.55	0.072
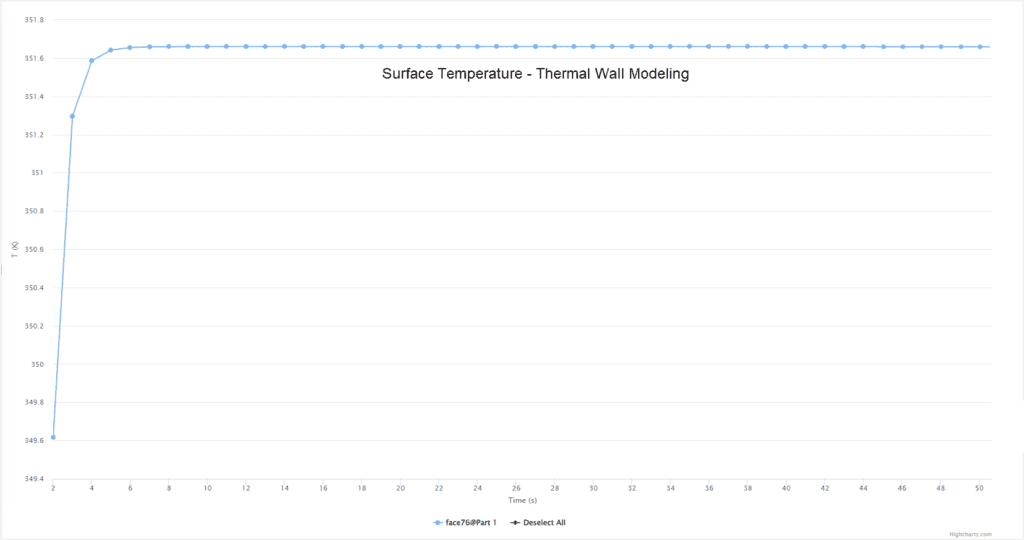
Thermal Wall Modeling	351.67	351.66	0.002

Convergence of Results

Convergence of the wall temperature without thermal wall modeling:

Convergence of the wall temperature with thermal wall modeling:

Temperature Distribution

Next, we take a look at the temperature distribution on the walls of the airbox:

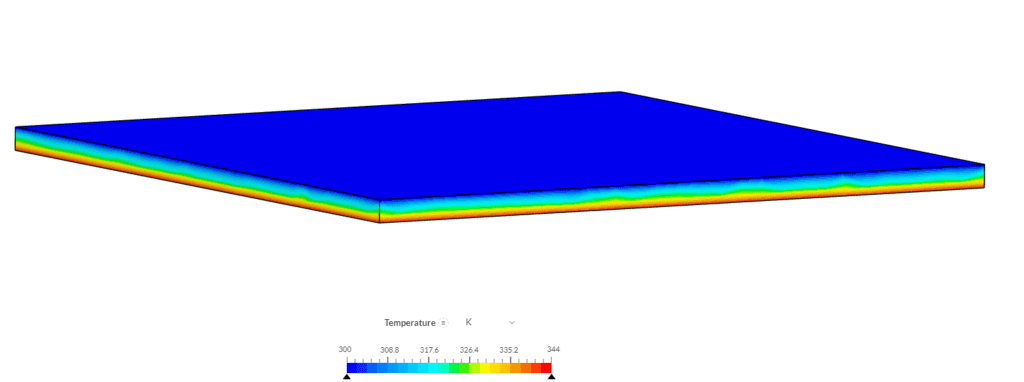
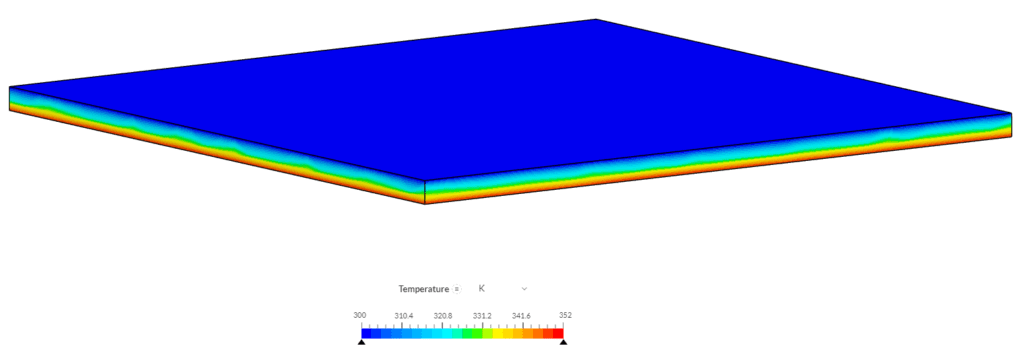
Overall the results obtained from the SimScale platform are in good agreement with the analytical solutions, and hence this serves as a good solar load validation for this feature.

Last updated: June 9th, 2022