Validation Case: Mach 2.0 Flow Over a 15 Degree Wedge

The aim of this validation is to compare the simulation results performed in SimScale using the compressible flow feature in its proprietary solver, Multi-purpose, with the simulation results in the study done by NASA titled, “Mach 2.0 Flow Over a 15 Degree Wedge${}^1$” as well as the analytical results ${}^2$.

The objective is to test the Multi-purpose solver’s ability to compute supersonic inviscid flows and in particular to capture oblique shock waves.

Geometry

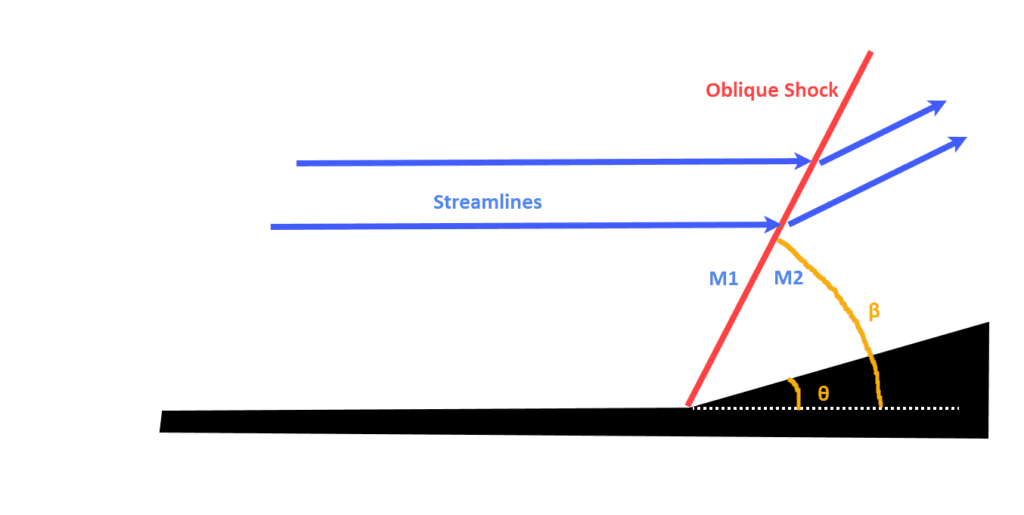
The geometry replicates a flow domain with an inviscid wedge. It has a tiny thickness to represent a two-dimensional flow. The geometry is inspired from the schematic${}^1$ as shown in Figure1:

For simulation purposes, since the wedge is symmetric about the x-axis only, one-half of the wedge is considered in the CAD geometry.

Analysis Type and Mesh

Analysis Type: Steady-state, Multi-purpose with k-epsilon and Compressible model

Mesh and Element Types:

The mesh was created with SimScale’s Multi-purpose mesh type, which is a body-fitted structured mesh. A manual sizing definition relative to the CAD was used.

Mesh Type	Minimum Cell Size	Maximum Cell Size	Cell Size on Surfaces	Number of cells	Element Type
Manual	1e-5 (relative to CAD)	0.004 (relative to CAD)	0.0025 (relative to CAD)	61868	3D Hexahedral

Simulation Setup

Material

Fluid:

• Air
  • Dynamic viscosity $(\mu )$: 1.83e-5 $kg/m.s$
  • Molar mass $(M_m)$: 28.97 $kg/kmol$
  • Prandlt number $Pr)$: 0.713
  • Specific heat $(C_p)$: 1004 $J/kg.K$

Boundary Conditions

Figure 4 shows the schematic of boundary conditions applied

Boundary Condition	Value
Velocity inlet $[m/s]$	686 (Fixed value with 527.4 $K$ total temperature)
Pressure outlet $[Pa]$	101325 (Fixed absolute static pressure)
Slip wall	1. Wedge to represent the inviscid boundary 2. Front and back faces to replicate a 2D flow
Symmetry	1. Upstream portion at the bottom 2. Top face

The symmetry boundary condition is used to simulate only one-half of the wedge (see Figure 1).

The total temperature at the inlet was calculated using the isentropic total temperature equation:

$$\begin{array}{}\text{(1)}& T_t=T(1+\frac{\gamma –1}{2}{M}^2)\end{array}$$

All the variable definitions can be found in Table 3.

Analytical Solution

The ratios for the Mach number, temperature, pressure, and density after and before the shock are given by the equations using wave theory.

$$\begin{array}{}\text{(2)}& \frac{P_2}{P_1}=1+\frac{2\gamma }{\gamma +1}(M_1^{2}si{n}^2\beta –1)\end{array}$$

$$\begin{array}{}\text{(3)}& \frac{{\rho }_2}{{\rho }_1}=\frac{(\gamma +1)M_1^{2}si{n}^2\beta }{(\gamma -1)M_1^{2}si{n}^2\beta +2}\end{array}$$

$$\begin{array}{}\text{(4)}& \frac{T_2}{T_1}=\frac{P_2}{P_1}\frac{{\rho }_1}{{\rho }_2}\end{array}$$

$$\begin{array}{}\text{(5)}& M_2=\frac{1}{sin(\beta -\theta )}\sqrt{\frac{1+\frac{\gamma –1}{2}{M}_1^{2}si{n}^2\beta }{\gamma M_1^{2}si{n}^2\beta –\frac{\gamma –1}{2}}}\end{array}$$

The shock angle $\beta$ is calculated using the equation

$$\begin{array}{}\text{(6)}& \tan \theta =2\cot \beta \frac{M_1^{2}si{n}^2\beta –1}{M_1^2(\gamma +\cos 2\beta )+2}\end{array}$$

Where,

Variable	Definition
$M$	Mach number
$T$	Temperature
$P$	Pressure
$\rho$	Air density
$\gamma$	Specific heat ratio
Subscripts 1, 2	1= before shock, 2 = after shock
$\beta$	Oblique shock angle
$\theta$	Wedge angle

Result Comparison

The result output from SimScale simulation is compared with the analytical results ${}^2$ as well as the Mach number contours obtained from the NASA study ${}^1$.

Analytical Comparison

To compute and compare the before and after shock quantities, probe points were added as shown in Figure 6 before the simulation run.

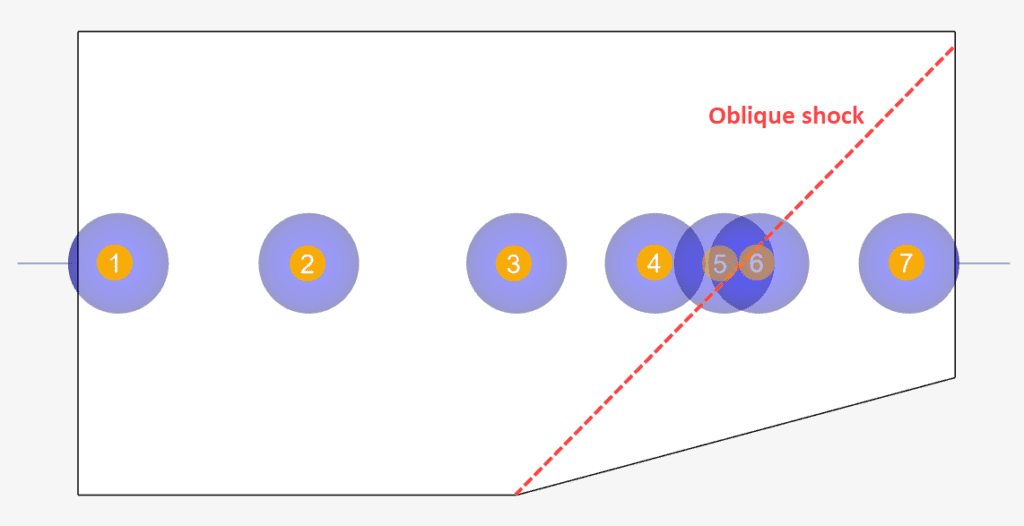
Using equations 2, 3, 4, and 5 the ratios of pressure, density, temperature, and Mach number are respectively compared against those obtained using probe points 5 and 6. These are given below:

Quantity	Analytical	SimScale	Error [%]
Static pressure ratio	2.1947	2.185	-0.44
Density ratio	1.7289	1.7239	-0.289
Temperature ratio	1.2694	1.267	-0.189
Mach number ratio	0.72285	0.7239	0.1457
Oblique shock angle	45.34°	~45°	~0

As it can be derived the Multi-purpose solver was able to accurately match the nature of the oblique shock as the ratios of the involved quantities before and after the shock compare well.

NASA Study Comparison

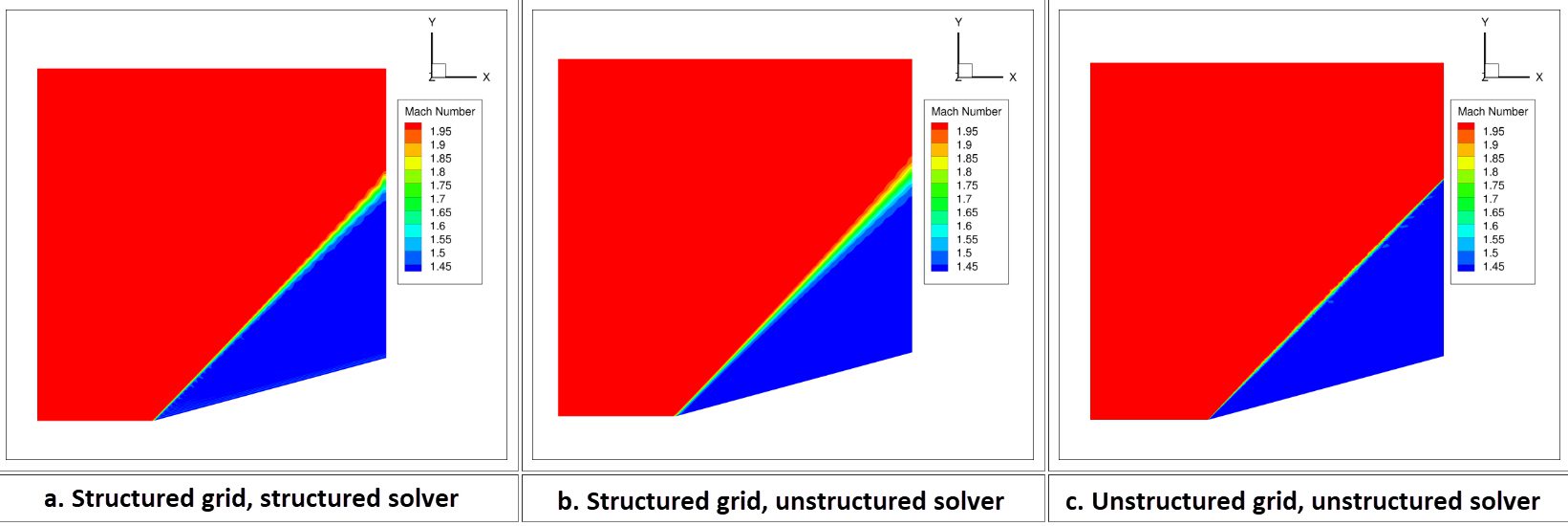
The NASA study${}^1$ compared eight separate cases using a combination of structured/unstructured grids with structured/unstructured solvers.

Depending on how the grid is clustered the shock wave is thin near the tip of the wedge and smears as it moves away from the wedge. This shock smearing is caused by the increase in the grid cell sizes away from the wedge surface. The solution obtained by the unstructured solver on the unstructured grid shows a very thin shock wave over the entire domain (Figure 7.c.). This is because the unstructured grid is clustered near the shock line throughout the domain.

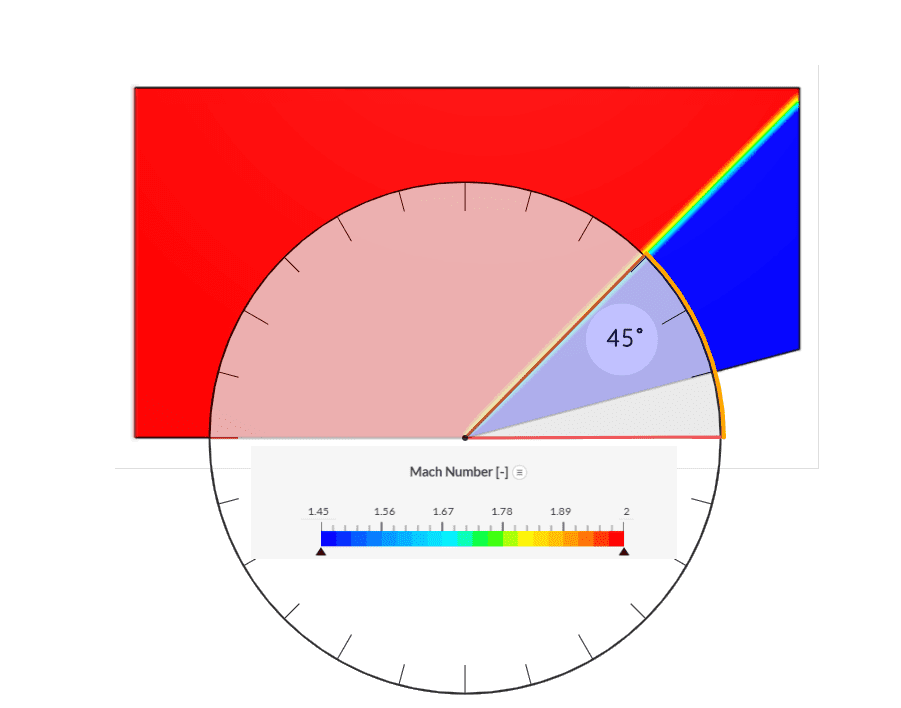
The Mach number contours obtained using SimScale’s Multipurpose solver show a similar trend as observed in Figure 8. The shock is thin at the tip and shows slight smearing as we move away. Further studies performed with finer mesh showed a decreasing diffusion trend and thinner shock.

The oblique shock is captured at an angle of ~45°. The legend was adjusted to match with those from the NASA study for ideal comparison.

Last updated: March 14th, 2025