Validation Case: Battery Pack Cooling

This validation case belongs to conjugate heat transfer, with the case of a battery pack cooling test. The aim of this project is to demonstrate the validity of SimScale’s CHTv2 solver by performing a conjugate heat transfer analysis of an air-cooled battery pack by comparing the following parameters:

Temperature of solid bodies
Temperature of fluid
Flow velocity profiles

The simulation results from SimScale were compared to the results presented in the reference paper [JILTE]\(^1\).

View Project

Geometry

The battery pack consists of a 3×3 cell configuration, as illustrated in Figure 1:

battery cell pack model simscale — Figure 1: Geometry model for the battery pack

The cell geometry dimensions are taken from the parameters given in the reference paper\(^1\), except for the cell’s top tab, whose proportions are approximated from the pictures. The value for the number of cells \((N)\) is 9. The dimension values are given in Table 1:

Parameter	Variable	Value \([mm]\)
Cell diameter	\(D\)	42.4
Cell height	\(H\)	97.7
Tab diameter	\(d\)	15
Tab height	\(h\)	3.7
Cell spacing	\(S_L\)	63.6
Enclosure width	\(W_E\)	212
Enclosure height	\(H_E\)	140.1

Table 1: Geometry parameters

Analysis Type and Mesh

Tool Type: OpenFOAM®

Analysis Type: Conjugate Heat Transfer v2

Mesh and Element Types:

The meshes were computed using the SimScale’s Standard meshing algorithm:

Mesh #	Mesh Type	Number of Cells	Setup
1	Standard	2829369	Fineness 7
2	Standard	2853925	Fineness 5, manual refinement 0.002 \(m\) and boundary layers
3	Standard	13970254	Fineness 5, manual refinement 0.001 \(m\) and boundary layers
4	Standard	4176543	Fineness 5, manual refinement 0.0015 \(m\) and boundary layers

Table 2: Mesh refinement per case

battery pack cooling mesh simscale — Figure 2: Standard mesh 1, clipped for showing the hexahedral core and tetrahedral surface. Such visualization can be created with the ‘Mesh quality‘ tool.

Simulation Setup

Model:

Flow compressibility: Incompressible/Compressible
Time dependency: Steady state
Turbulence model: Laminar
Incompressible Working Fluid (Air):
- (\(\nu\)) Kinematic viscosity: 1.529e-5 \(m^2/s\)
- (\(\rho\)) Density: 1.196 \(kg/m^3\)
- Thermal expansion coefficient: 3.43e-3 \(1/K\)
- (\(T_0\)) Reference temperature: 273.1 \(K\)
- (\(Pr_{lam}\)) Laminar Prandtl number: 0.713
- (\(Pr_{t}\)) Turbulent Prandtl number: 0.85
- Specific heat: 1004 \(J/(kg.K)\)
Compressible Working Fluid (Air):
- (\(M_m\)) Molar mass: 28.97 \(kg/kml\)
- Transport: Const
- (\(\mu\)) Dynamic viscosity: 1.83e-5 \(kg/s.m\)
- (\(Pr\)) Prandtl number: 0.713
- (\(Pr_{t}\)) Turbulent Prandtl number: 0.85
- Thermal model: hConst (Constant entalphy)
- Specific heat: 1004 \(J/(kg.K)\)
- Equation of state: Perfect gas
Solid Material (Cells):
- Conductivity type: Isotropic
- (\(\kappa\)) Thermal conductivity: 1 \(W/(m.K)\)
- Specific heat: 837.4 \(J/(kg.K)\)
- Equation of state: Constant density
- (\(\rho\)) Density: 2008 \(kg/m^2\)

Two simulations were run using the compressible fluid model, in order to test the accuracy of the Boussinesq approximation in the incompressible solver.

Boundary Conditions:

Velocity Inlet: 0.1 \(m/s\)
Pressure Outlet: 101 325 \(Pa\) – Fixed value
Absolute power source on cells: 0.35 \(W\)
External walls: No slip flow, adiabatic.

Reference Solution

The reference solution for the battery pack cooling is of the numerical type, as developed in [JILTE]\(^1\). It was computed using the Ansys FLUENT 6.3 CFD package. The reference simulation is transient, thus approximations were required to compare the results to SimScale’s steady-state CHT v2 solver.

The reference solutions are the temperature and velocity fields, measured at different locations:

Area average temperatures at cells 4, 5 and 6 (refer to Figure 3).
Converged temperature profile in two planes perpendicular to the flow direction, between rows 1 and 2 (Plane 1) and between rows 2 and 3 (Plane 2) of the cells. The profile is reported along lines at two different heights in the planes, 25 and 50 \(mm\).
Flow velocity magnitude profile for Plane 1 at heights as described above.

locations where results for lpu battery pack cooling are analyzed — Figure 4: Illustration of planes and heights at which the data will be analyzed

Results Comparison

For the average temperature across cells, the comparison of the different meshes shows the convergence behavior:

Temperature Location	Mesh 1 \([°C]\)	Mesh 2 \([°C]\)	Mesh 3 \([°C]\)	Mesh 4 \([°C]\)	Final Deviation
Cell 4 Average	25.20	25.20	26.60	26.30	1.14 %
Cell 5 Average	27.50	26.70	28.60	28.60	0.00 %
Cell 6 Average	27.40	27.10	28.90	28.90	0.00 %

Table 3: Temperature results \((°C)\) for the mesh convergence study. Final deviation is between Mesh 3 and Mesh 4.

It was found that Mesh 4 is optimal because it captures the converged results while using a smaller cell count than mesh 3.

Comparison of the computed values in SimScale with Mesh 3 (finest) and the reference solution is shown below:

Temperature Location	SimScale Result (Mesh 3)	Reference Result	Deviation
Cell 4 Average	26.60	27.17	-2.10 %
Cell 5 Average	28.60	27.32	4.69 %
Cell 6 Average	28.90	27.18	6.33 %

Table 4: Comparison of temperature results \((°C)\) against the reference values\(^1\)

A maximum temperature deviation of 1.7 \(°C\) is observed at Cell 6, between SimScale and the reference results. This corresponds to an error of 6.33% in the battery pack cooling strategy.

The temperature profiles comparison in Plane 1 is presented at two heights, 25 and 50 \(mm\). ‘Reference’ curves correspond to the paper results, and ‘SimScale’ curves correspond to the Mesh 3 results.

battery pack cooling temperature results simscale — Figure 5: Comparison of temperature profiles at Plane 1

The same comparison is performed for Plane 2:

The deviation of air temperature with respect to reference values is within 2 \(°C\). Similar to cell temperatures, air temperature values are mostly over predicted.

The comparison of flow velocity magnitude profiles for Plane 1 is presented below:

battery pack cooling velocity results simscale — Figure 7: Comparison of flow velocity magnitude profiles at Plane 1

The maximum velocity values are over-predicted by SimScale by a maximum of around 0.06 \(m/s\). This error can be attributed to the comparison of steady-state to transient results.

Finally, for the verification of the Boussinesq approximation, the temperature and velocity profiles are compared for results of runs using compressible and incompressible flow models. The velocity magnitude and temperature profiles are presented for Plane 1:

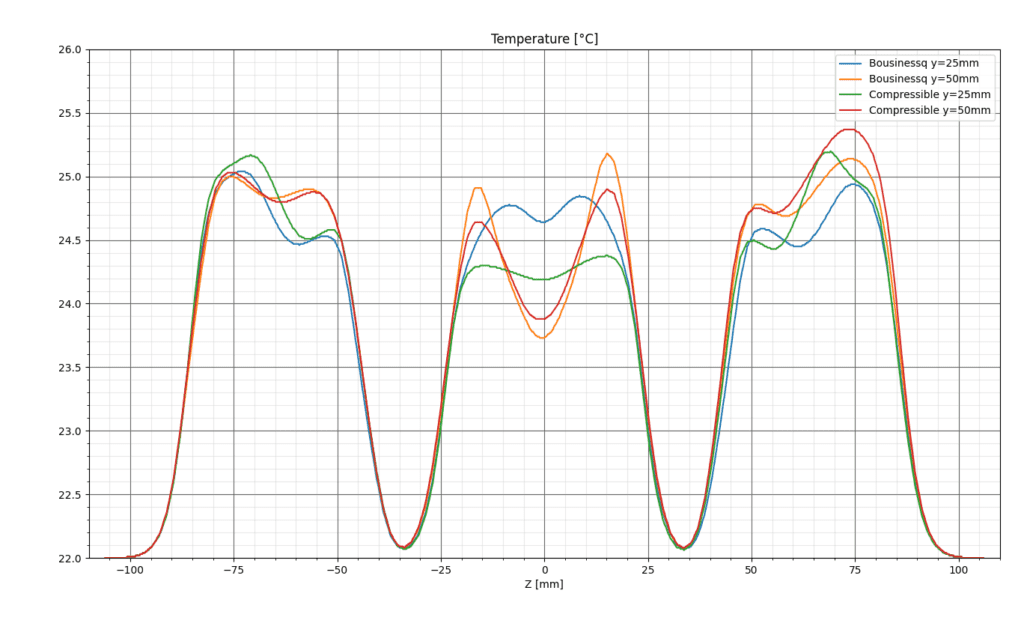
boussinesq temperature results simscale — Figure 8: Temperature profiles for the incompressible model using Boussinesq approximation and compressible flow model

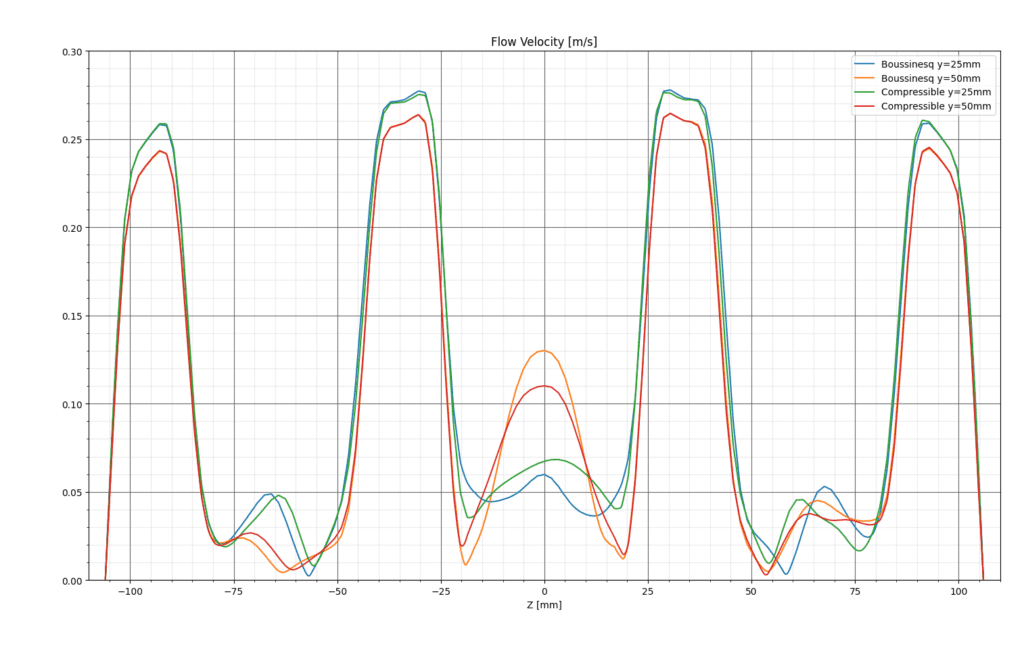
boussinesq velocity results simscale — Figure 9: Velocity magnitude profiles for incompressible model using Boussinesq approximation and compressible flow model

Good correlation is achieved between profiles using Boussinesq approximation and compressible flow, thus it is determined that the air velocity profile is independent of the approximation.

temperature and velocity results simscale — Figure 10: Temperature of the cells and flow velocity at 50 \(mm\) height

References

R.D. Jilte, Raviden Kumar – Numerical investigation on cooling performance of Li-ion battery thermal management system at high galvanostatic discharge – Engineering Science and Technology, an International Journal – Elsevier – Octuber 2018

Note

If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.

Last updated: June 7th, 2021

Did this article solve your issue?

How can we do better?

We appreciate and value your feedback.