websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Static Analysis of an I-Beam Under Remote Force

    Validation Case: Static Analysis of an I-Beam Under Remote Force

    This validation case belongs to solid mechanics. This test case aims to validate the following parameters:

    The simulation results of SimScale were compared to the results derived from [Roark]\(^1\).

    View Project

    Geometry

    The geometry used for the case is as follows:

    geometry model static analysis of i-beam
    Figure 1: Geometry model of an I beam

    The beam has a length \(L\) of 1 \(m\), with the cross-section dimensions as shown:

    cross section parameters static analysis of i beam under remote force validation case
    Figure 2: Beam cross-section dimensions parameters
    ParameterValue [\(m\)]
    B0.06
    H0.08
    b0.04
    h0.06
    Table 1: Cross-section geometry parameters

    Analysis Type and Mesh

    Tool Type: Code_Aster

    Analysis Type: Static Linear

    Mesh and Element Types:

    Tetrahedral meshes were computed using SimScale Standard mesh algorithm and manual sizing. The table below shows an overview of the mesh characteristics.

    CaseMesh TypeNumber of
    Nodes    		Element Type
    AStandard 33451st order tetrahedral
    BStandard207422nd order tetrahedral
    Table 2: Number of mesh nodes and types of elements for each case
    tetrahedral mesh static analysis of i beam under remote force validation case
    Figure 3: Second order tetrahedral mesh used in case B

    Simulation Setup

    Material:

    • Linear Elastic Isotropic:
      • \( E = \) 205 \(GPa \)
      • \( \nu = \) 0.28

    Boundary Conditions:

    • Constraints:
      • Face A is fixed
    • Loads:
      • Remote force of 1000 \(N\) applied at a distance \(d = \) 1 \(m\) on face B
    remote force static analysis of i-beam validation
    Figure 4: Remote force diagram showing the applied load on the beam

    Reference Solution

    The analytical solutions for the deflection \(w\) at the free end of the beam are given by the following equations. The remote force \(F\) is substituted with a force and moment pair \(M\):

    $${M = Fd} \tag{1}$$

    $$ w = \frac{F L^3}{3 E I} + \frac{M L^2}{2 E I} \tag{2} $$

    $$ I = \frac{1}{12} ( B H^3 – b h^3) \tag{3} $$

    The computed reference solution is:

    $$ M = 1000\ Nm $$

    $$ I = 1.84×10^{-6}\ m^4 $$

    $$ w = 2.209×10^{-3}\ m $$

    Result Comparison

    Comparison of displacement DZ of the center point of face B with the computed reference solution \(w\):

    CASEDZ
    [\(10^{-3}\ m\)]    		\(w\)
    [\(10^{-3}\ m\)]    		Error
    A2.141092.2093.07 %
    B2.21212.209-0.14 %
    Table 3: Deflection results comparison

    Comparison of the neutral fiber deflection shapes:

    neutral fiber deflection static analysis of i-beam
    Figure 5: Neutral fiber deflection comparison for analytical and computed solutions

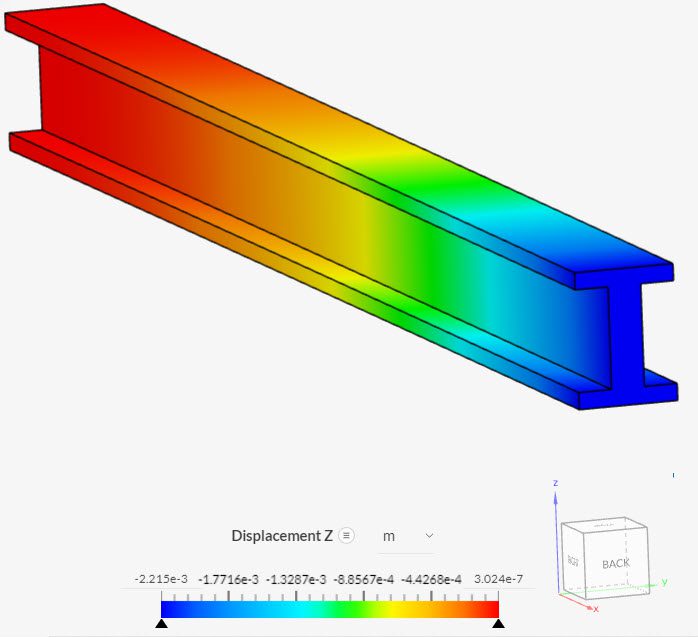
    And finally, a plot showing the deformed shape and the magnitude of DZ displacement:

    deformed and colored shape plot static analysis of i beam under remote force validation case
    Figure 6: Case B, showing the deformed shape of the beam with contours for the displacement in the z-direction

    References

    • (2011) “Roark’s Formulas For Stress And Strain, Eighth Edition”, W. C. Young, R. G. Budynas, A. M. Sadegh

    Note

    If you still encounter problems validating your simulation, then please post the issue on our forum or contact us.

    Last updated: September 9th, 2022

    Contents