Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Hollow Cylinder in Plane Strain Condition

    Validation Case: Hollow Cylinder in Plane Strain Condition

    This plane strain condition validation case belongs to solid mechanics. This test case aims to validate the following parameters:

    • Distributed pressure
    • Symmetry boundary condition
    • Nodal displacement
    • Strains and Nodal stresses

    The simulation results from SimScale were compared to the analytical results presented in [SSLV04]\(^1\).

    View Project

    Geometry

    The geometry used for the case is as follows:

    hollow cylinder geometry
    Figure 1: Hollow cylinder geometry wireframe

    The 3D geometry is a 45-degree section of a hollow cylinder with dimensions as tabulated below:

    ABEFA’B’E’F’
    x0.10.20.07070.14140.10.20.07070.1414
    y000.07070.1414000.07070.1414
    z00000.010.010.010.01
    Table 1: Geometry dimensions in meters

    Analysis Type and Mesh

    Tool Type: Code Aster

    Analysis Type: Static linear

    Mesh and Element Types: The meshes used in this project were created using the standard meshing tool on the SimScale platform. In Table 2 you will find a summary of the mesh characteristics.

    CaseMesh TypeNumber of NodesElement Type
    (A)Standard325531st order tetrahedral
    (B)Standard2394212nd order tetrahedral
    Table 2: Mesh characteristics

    Find below the manually refined 1st order standard mesh used in case A:

    linear standard mesh in simscale for plane strain validation case
    Figure 2: First order standard mesh used for case A

    Simulation Setup

    Material:

    • Steel (linear elastic)
      • \(E\) = 200 \(GPa\), \(v\) = 0.3

    Boundary Conditions:

    • Constraints
      • Face EFE’F’ zero normal-displacement
      • Face ABA’B’ zero y-displacement
      • Face ABEF and face A’B’E’F’ zero z-displacements fixed
    • Loads
      • The pressure of 60 \(MPa\) on Face AEA’E’

    Reference Solution

    The analytical solution is given by the equations presented under Reference Solution\(^1\).

    Result Comparison

    The results obtained from SimScale for displacements, stresses, and strains at point A are compared with those presented in SSLV04.

    CaseQuantity[SSLV04]SimScaleError [%]
    (A)Displacement \(dx\ [m]\)5.90e-055.72e-05-3.05
    (B)Displacement \(dx\ [m]\)5.90e-055.72e-05-3.05
    (A)Cauchy Stress \(\sigma_{xx}\ [MPa]\)-6.00e01-5.89e01-1.83
    (B)Cauchy Stress \(\sigma_{xx}\ [MPa]\)-6.00e01-5.99e01-0.16
    (A)Cauchy Stress \(\sigma_{yy}\ [MPa]\)1.00e021.00e020
    (B)Cauchy Stress \(\sigma_{yy}\ [MPa]\)1.00e021.00e020
    (A)Total Strain \(\epsilon_{xx} \)-4.50e-04-4.63e-042.89
    (B)Total Strain \(\epsilon_{xx} \)-4.50e-04-4.67e-043.78
    (A)Total Strain \(\epsilon_{yy} \)5.90e-045.72e-04-3.05
    (B)Total Strain \(\epsilon_{yy} \)5.90e-045.72e-04-3.05
    Table 3: Comparison of results at point A

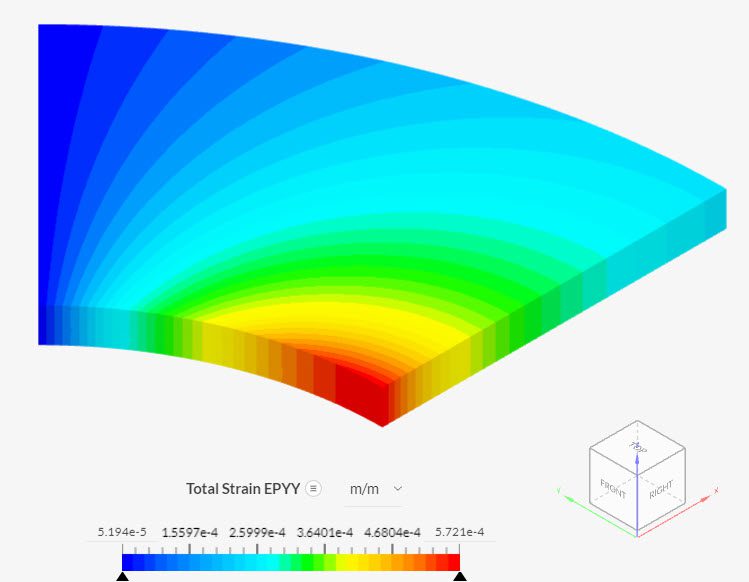
    Find in Figure 3 below the case B results for the total strain \(\epsilon_{yy}\) distributed across the cylinder:

    contours of strain simscale post processing
    Figure 3: Contours of total strain \(\epsilon_{yy} \) acting on the hollow cylinder under a plane strain condition.

    References

    Last updated: July 21st, 2021

    Contents