websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Heat Transfer in an Electronics Design

    Validation Case: Heat Transfer in an Electronics Design

    This case belongs to solid mechanics. The aim of this test case is to validate the following parameters within the components of an electronics design:

    • Transient change in temperature with respect to ambient temperature.

    The simulation results of SimScale are compared to the results presented in [Bruce]\(^1\).

    View Project

    Geometry

    The geometry used for the case is as follows:

    simulation ready geometry cad model workbench
    Figure 1: Simulation ready CAD model

    A more descriptive schematic of the components explains the configuration as shown in Figure 2:

    ic electronics package lid die pcb tim heat sink base configuration
    Figure 2: High-power IC package geometry

    The analysis is carried out on a high-power IC package that is attached between the heatsink base and the PCB substrate. The components explicitly represented in the simulation model are the die, TIM 1, lid, TIM 2, and the heat sink base (where TIM = Thermal Interface Material). These components are shown inside the dashed square box above.

    The following table displays the dimensions of each component in the electronics design:

    ComponentLength \([mm]\)Width \([mm]\)Thickness \([mm]\)
    Die13130.50
    TIM 113130.10
    Lid13130.50
    TIM 213130.05
    Heat sink base13136.00
    Table 1: The dimensions of the model’s components

    Analysis Type and Mesh

    Tool type: Code_Aster

    Analysis type: Heat transfer, Non-linear

    Time dependency: Transient

    Mesh and element types: SimScale’s Standard algorithm was used to generate the mesh for the electronics design.

    Meshing algorithmNo. of nodesNo. of volumesMesh Elements
    Standard38694184359Tetrahedral/Hexahedral
    Table 2: Details of the IC package mesh

    The final mesh can be seen below:

    standard meshing algorithm electronics design
    Figure 3: The final mesh consisting of tetrahedral and hexahedral elements.

    Simulation Setup

    Material:

    • Isotropic with the following specifications for each part:
    ComponentMaterialThermal conductivity \([ \frac{W}{m\ K}] \) Density \([\frac{kg}{m^3}]\) Specific heat \([\frac{J}{kg\ K}] \)
    Die Silicon1112330668
    TIM1Ag-Epoxy2.04400400
    LidCopper3908890385
    TIM2Grease Aluminium filler particle1.02500900
    Heat sink baseCopper3908890385
    Table 3: Material properties for each component

    Initial conditions:

    • Temperature \(T\) = 273.15 \(K\)  

    Boundary conditions:

    • Heat flux loads:
      • Surface heat flux:
        A power of 1 \(W\) is applied to the top surface of the die which is in contact with TIM 1. Therefore, the resulting surface heat flux at this surface is calculated by dividing the power with respect to the die surface area.
        Surface heat flux = 1/(169e-6) = 5917.1598 \(W \over \ m^2\)
      • Convective heat flux:
        The cooling effect of the heatsink fins is collectively represented through a heat transfer coefficient that is directly applied to the heatsink base (top surface of the geometry). Therefore, a convective heat flux boundary condition is used to represent the thermal resistance offered by the heatsink to the surrounding air.
        Convective heat flux = 20000 \(W \over \ m^2 \ K\)

    Electronics Design Result Comparison

    The temperature distribution of the IC package is as shown below:

    temperature distribution IC package
    Figure 4: Temperature distribution as seen in the SimScale’s post processor.

    The comparison of SimScale results with that of [Bruce]\(^1\) for the die, lid, and heat sink is shown below:

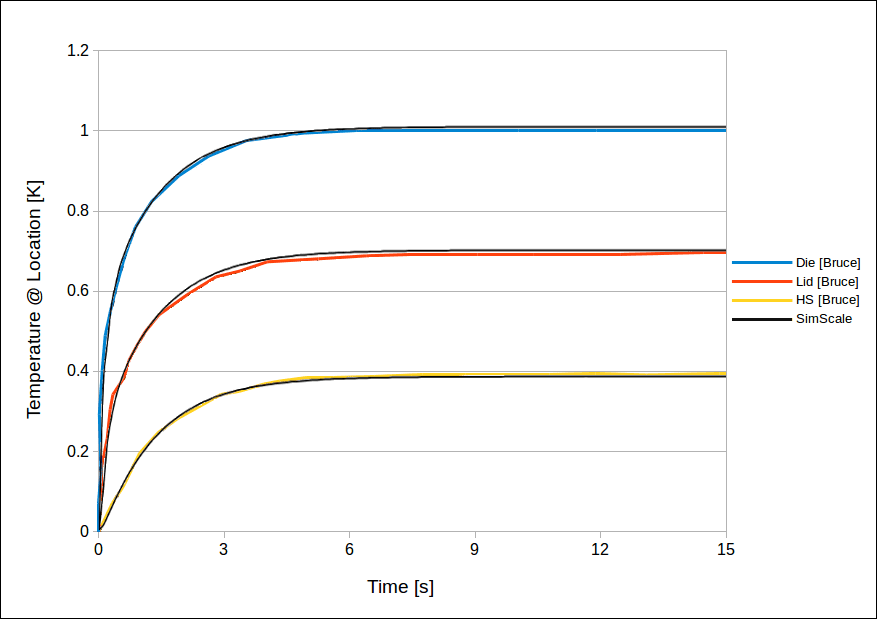
    temperature distribution ambient results comparison ic package heat transfer
    Figure 5: Temperature change w.r.t ambient temperature versus time plot comparison with [Bruce]

    The results are calculated by deducting the initial temperature condition of 273.15 \(K\) from the average temperature value of each area for 150 timesteps.
    A slight deviation in the temperature graphs comparison above is due to the approximation error caused during the extraction of temperature values from the digital plots.

    References

    Last updated: May 20th, 2021

    Contents