This validation case belongs to solid mechanics. The aim of this test case is to validate the following parameters on a fixed beam, that is subjected to a temperature change of 10 \(K\):
The simulation results of SimScale were compared to the results presented in [Roark]\(^1\).
A bar with a square cross-section was used for this case:
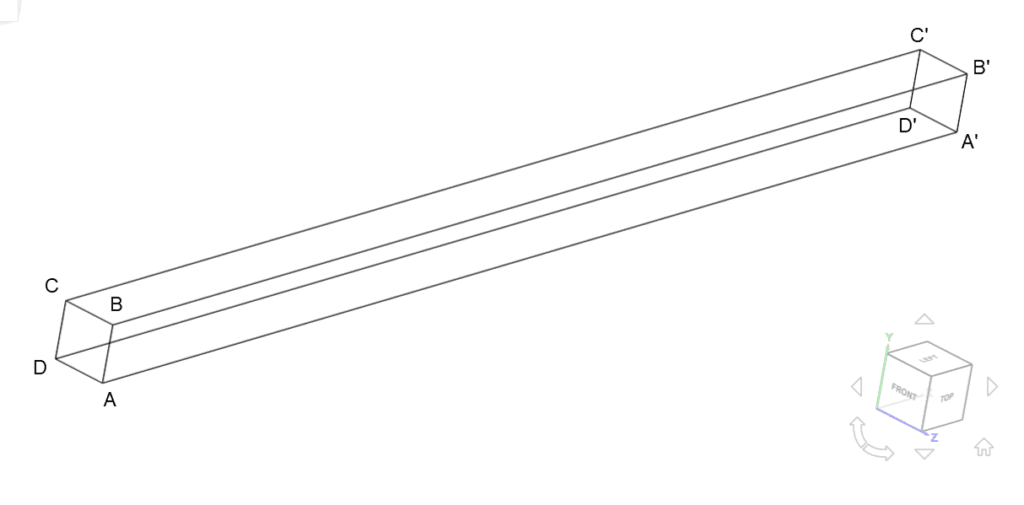
The cross section area of the bar is \(A\) = 0.05 x 0.05 \(m^2\) and it’s length is \(l\) = 1.0 \(m\).
Tool Type: Code_Aster
Analysis Type: Thermomechanical, linear with static inertia effect
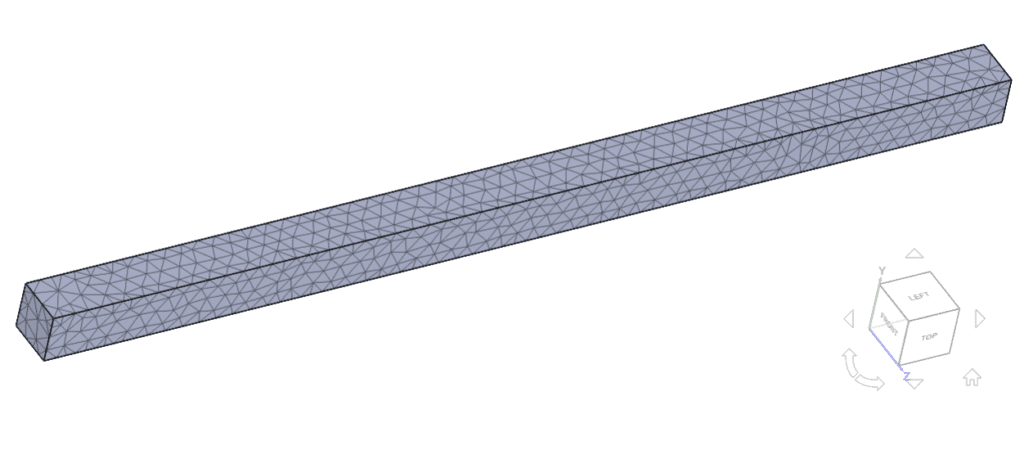
Mesh and Element Types:
The meshes used in (A) and (B) were created with the Standard mesher tool on the SimScale platform. Details can be found in Table 1:
| Case | Mesh type | Number of nodes | Element type |
| A | Standard | 1484 | 1st order tetrahedral |
| B | Standard | 9320 | 2nd order tetrahedral |
Material:
Boundary Conditions:
The analytical solution for the unit stress is given by the following equation:
$$σ =ΔT \times \ γ \times \ E $$
where:
As a result, the analytical calculation gives a unit stress of: $$σ =24.6\ MPa $$
Comparison of the unit stress \(\sigma\) obtained from SimScale against the reference results obtained from [Roark]\(^1\) is given in the following table:
| Case | [Roark] \([MPa]\) | SimScale \([MPa]\) | Error \([\%]\) |
| A | 24.6 | 24.6 | 0.00 |
| B | 24.6 | 24.6 | 0.00 |
As shown in Table 2, the SimScale results perfectly match the analytical ones with 0.00% error.
Last updated: July 21st, 2021
We appreciate and value your feedback.
