websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Elastoplastic Notched Plate

    Validation Case: Elastoplastic Notched Plate

    This validation case belongs to solid mechanics. It aims to validate the following parameters:

    • Plastic material behavior
    • Reduced integration element type

    The simulation results of SimScale were compared to the reference values presented in [SSNP123]\(^1\).

    View Project

    Geometry

    Find below the notched plate geometry used for this validation case:

    notched plate geometry validation simscale
    Figure 1: Notched plate geometry used in the present validation case

    The plate dimensions are tabulated below:

    ABCDEF
    x00.0040.0050.00500
    y000.0010.0050.0050.001
    z0.00010.00010.00010.00010.00010.0001
    Table 1: Geometry dimensions in meters

    The corresponding nodes marked with an apostrophe (‘) are translated 0.0001 \(m\) along the negative z-direction.

    Analysis Type and Mesh

    Tool Type: Code_Aster

    Analysis Type: Nonlinear static

    Mesh and Element Types: The meshes used in this project were created in SimScale with the standard algorithm.

    CaseElement TypeNumber of NodesElement Technology
    (A) 2nd Order Tetrahedral44211Standard
    (B) 2nd Order Tetrahedral 44211Reduced integration
    Table 2: Mesh characteristics

    Find below the mesh used for cases A and B. It’s a standard mesh with second-order tetrahedral cells.

    tetrahedral second order mesh notched plate
    Figure 2: Second order standard mesh used for cases A and B

    Simulation Setup

    Material:

    • Steel (plastic behavior)
      • \(E\) = 200 \(GPa\), \(v\) = 0.3
      • \(\rho\) = 7870 \(kg/m^3\)
      • \(\sigma_y\) = 200 \(MPa\), \(E_T\) = 1000 \(MPa\), as shown below:
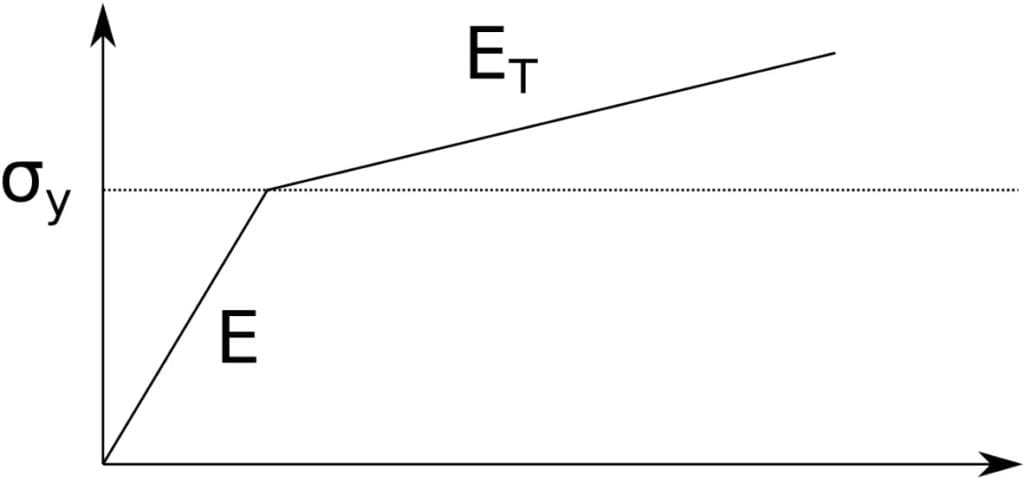
    young's modulus plastic behavior
    Figure 4: Dependency of the Young’s modulus

    Boundary Conditions:

    • Constraints
      • \(d_x\) = 0 on face AA’E’EF
      • \(d_y\) = 0 on face AA’B’B
      • \(d_z\) = 0 for all nodes
      • Face EE’D’D: displacement of 0.0001 \(m\) in the positive y-direction

    Result Comparison

    The results obtained from SimScale for the Cauchy stress \(\sigma_{yy}\) along the FC line are compared to the values of reference from [SSNP123]\(^1\). These values of reference were extracted with WebPlotDigitizer. Figure 5 shows the results for case A, where element technology is set to standard:

    notched plate validation results standard elements
    Figure 5: Comparison of case A with the reference values from [SSNP123]¹

    Similarly, for case B, where reduced integration was used:

    notched plate validation results reduced integration elements
    Figure 6: Comparison of case B with the reference values from [SSNP123]¹

    In both Figures 5 and 6, SimScale’s results show good agreement with the reference values.

    Inspecting the Cauchy stress \(\sigma_{yy}\) for case B in the post-processor:

    notched plate validation post processing contours
    Figure 7: Case B, showing the contours for Cauchy stress σyy, in SimScale’s post-processor

    References

    Last updated: November 7th, 2023

    Contents