websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Butterfly Valve with Multi-purpose solver

    Validation Case: Butterfly Valve with Multi-purpose solver

    This validation case belongs to fluid dynamics and the aim of this case is to validate the following parameters inside a pipe with a butterfly valve:

    • Pressure drop using the Multi-purpose solver in SimScale

    The simulation results of SimScale were compared to the results presented in the study done by Song, Xue Guan, and Park, Young Chui with the title “Numerical Analysis of Butterfly Valve – Prediction of Flow Coefficient and Hydrodynamic Torque Coefficient“\(^1\).

    View Project

    Geometry

    The model used in this validation case is a pipe with a disc-shaped butterfly valve inside, which can be seen below:

    butterfly valve at 20 degrees inside pipe
    Figure 1: Pipe model with butterfly valve inside the opening at 20° angle

    The dimensions of the pipe can be seen in the table below:

    DimensionValue \([m]\)
    Upstream length14.4
    Downstream length27
    Valve & pipe diameter (D)1.8
    Valve maximum thickness0.36
    Table 1: Pipe and valve dimension

    9 variants of valve opening angles ranging from 20° to 85° were used as a comparison to the reference study.

    Analysis Type and Mesh

    Analysis Type: Steady-state, Multi-purpose with K-Epsilon turbulence model

    Mesh and Element Types: The mesh was created with SimScale’s Multi-purpose mesh type.

    Mesh Sensitivity

    The Multi-purpose meshing algorithm with hexahedral cells was used to generate the mesh. For this simulation, refinement level 8 was chosen for the comparison of different valve openings.

    Mesh TypeNumber of cellsElement Type
    Automatic Level 8990003D Tetrahedral/Hexahedral
    Table 2: Mesh data for butterfly valve validation case
    Mesh Valve opening angle 50 deg cutting plane butterfly valve Multi-purpose
    Figure 2: Mesh within the flow domain with fineness level 8
    Mesh Valve opening angle 50 deg ISO butterfly valve Multi-purpose
    Figure 3: Multi-purpose meshing performed on the valve with refinement around the edge of the valve

    Simulation Setup

    Fluid:

    • Water
      • Kinematic viscosity \((\nu)\): 9.338e-7 \(m^2/s\)
      • Density \((\rho)\): 997.3 \(kg/m^3\)

    Boundary Conditions:

    boundary condition overview butterfly valve Multi-purpose
    Figure 4: Boundary condition overview where the flow goes from left to right

    The boundary conditions are the same for all opening angles and were assigned as shown in Table 3:

    Boundary ConditionValue
    Velocity inlet3 \(m/s\)
    Pressure outlet0 \(Pa\)
    No-slip wallPipe walls and valve surface
    Table 3: Boundary conditions for pipe and valve

    Reference Solution

    The reference solution for the flow coefficient and the torque coefficient is given in the following formulae:

    Flow coefficient:

    $$c_v = Q \sqrt{\frac{S_g}{\Delta P}} \tag{1}$$

    where:

    • \(c_v\): flow coefficient
    • \(Q\): flow discharge \((GPM-Gallons\,per\,minute)\)
    • \(\Delta P\): pressure drop \((psi)\)
    • \(S_g\): specific gravity of water

    Torque coefficient:

    $$c_t = \frac{T(x)}{\Delta P \times d^3} \tag{2}$$

    where:

    • \(c_t\): torque coefficient
    • \(T(x)\): torque in the x-axis \((N.m)\)
    • \(\Delta P\): pressure drop \((psi)\)
    • \(d\): diameter of pipe \((in)\)

    Result Comparison

    Comparison of the flow coefficient obtained from SimScale against the reference results obtained from [1] is given below:

    Valve validation Flow Coefficient _ Valve Opening Angle -Multi-purpose
    Figure 5: Flow coefficient comparison between reference results and SimScale

    Deviation to Reference

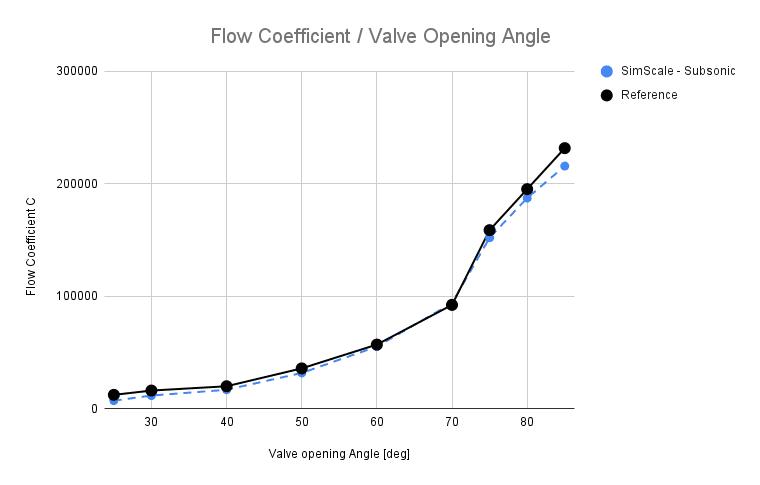
    Deviation of the results gained from SimScale in comparison to the results obtained from [1] can be seen in Figure 6. The deviation gets very close to the reference results for the opening angle from 50-70 degrees. It has to be noted that small valve opening angles are deviating highly, which is expected according to Song, Xue Guan, and Park, Young Chui\(^1\).

    However, it must be noticed that at valve opening smaller than 20 degrees, the minimum error between CFX simulation and experimental data reach to 49.27958%.

    Song, Xue Guan and Park, Young Chui Reference [1]
    deviation percentage against valve opening angle
    Figure 6: Deviation of SimScale results in comparison to the experimental data.

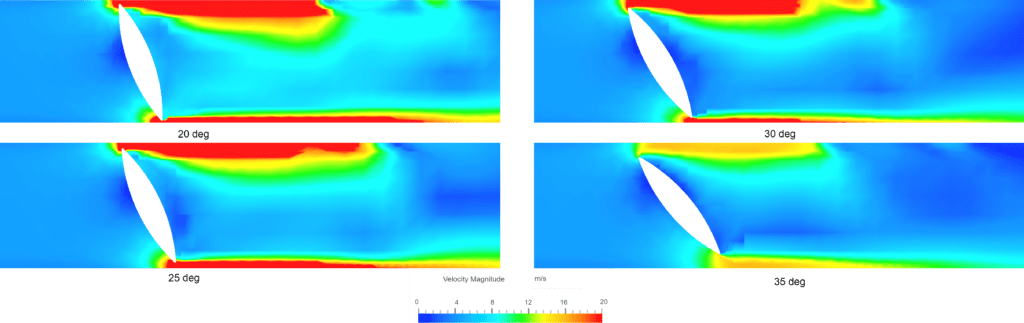
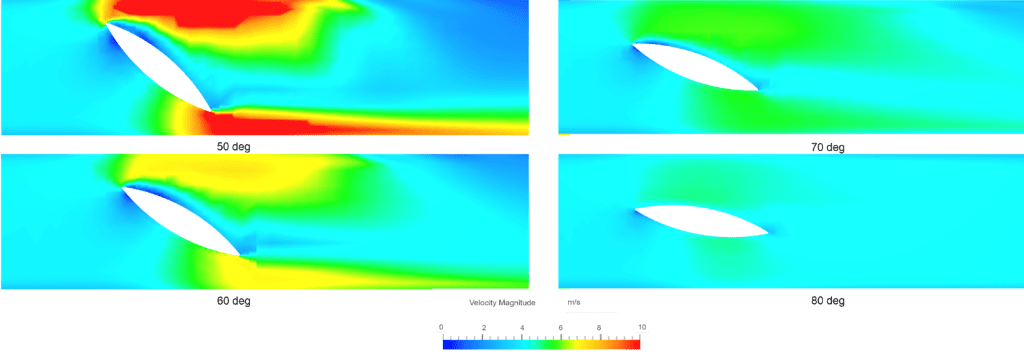
    The flow contours inside the pipe when the valve is opened at the simulated opening angles as observed in our online post-processor:

    Valve comparison subsonic Validation Velocity 20 -35 deg
    Figure 7: Velocity magnitude contours inside the pipe at the centerline when the valve is opened at a 20° – 35° angle.
    Valve comparison subsonic Validation Velocity 50-80 deg
    Figure 8: Velocity magnitude contours inside the pipe at the centerline when the valve is opened at a 50° – 80° angle.

    References

    Note

    If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.

    Last updated: September 23rd, 2024

    Contents