Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    Start Simulating Now

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Bonded Contact on a Quarter Shaft

    Validation Case: Bonded Contact on a Quarter Shaft

    This bonded contact validation case belongs to solid mechanics. This test case aims to validate the following parameter:

    • Bonded contact

    The simulation results obtained with SimScale were compared to the analytical results presented in [Roark]\(^1\).

    View Project

    Geometry

    Two geometries are used for this bonded contact validation. The first one consists of a quarter shaft. Radius is 0.1 \(m\) and length is 0.5 \(m\):

    quarter shaft validation simscale
    Figure 1: Quarter shaft consisting of a single part

    The second geometry has the same dimensions, however, it is split exactly in half, between the ABC and A’B’C’ planes:

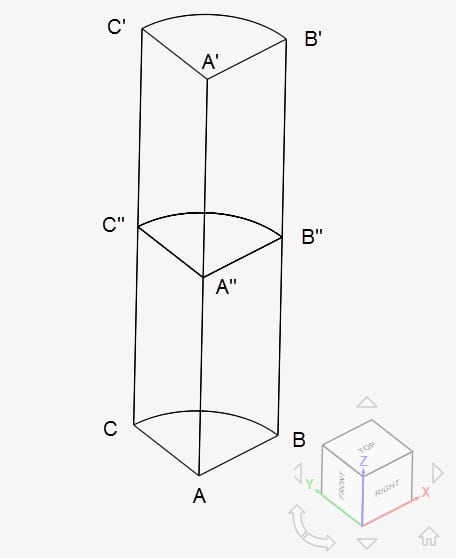
    bonded contact validation shaft
    Figure 2: Quarter shaft geometry, consisting of two parts

    The 3D geometry is a 90\(^0\) section of a cylinder with dimensions as tabulated below:

    ABCA’B’C’A”B”C”
    x00.1000.1000.10
    y000.1000.1000.1
    z0000.50.50.50.250.250.25
    Table 1: Geometry dimensions in meters

    Analysis Type and Mesh

    Tool Type: Code Aster

    Analysis Type: Linear static

    Mesh and Element Types: The meshes for Cases A through D were created in SimScale. The standard algorithm was used.

    CaseGeometryElement TypeNumber of NodesElement Technology
    (A)Quarter Shaft1st Order Tetrahedral8660Standard
    (B)Quarter Shaft – Split1st Order Tetrahedral 8846Standard
    (C)Quarter Shaft2nd Order Tetrahedral 62943Reduced Integration
    (D)Quarter Shaft – Split2nd Order Tetrahedral 63772Reduced Integration
    Table 2: Mesh characteristics

    Find below the mesh used for Case D. It is a standard mesh with second-order tetrahedral cells.

    tetrahedral second order mesh
    Figure 3: Mesh used for Case D

    Simulation Setup

    Material:

    • Steel (linear elastic)
      • \(E\) = 208 \(GPa\), \(v\) = 0.3
      • Therefore, the shear modulus is 80 \(GPa\).

    Boundary Conditions:

    • Constraints
      • Fixed support on face ABC
      • Face A’B’C’ is rotated with an angle \((\theta)\) of 2e-4 \(rad\)
    • Contacts
      • Single part shaft
        • Cyclic symmetry: face AA’B’B is tied to face AA’C’C. Rotation axis: z-axis. Sector angle: 90º
      • Split shaft
        • Cyclic symmetry: face AA”B”B is tied to face AA”C”C. Rotation axis: z-axis. Sector angle: 90º
        • Cyclic symmetry: face A”A’B’B” is tied to face A”A’C’C”. Rotation axis: z-axis. Sector angle: 90º
        • Bonded contact: both parts are bonded at A”B”C”.

    Reference Solution

    The analytical solution for maximum shear stress \(\tau_{max}\) given below is based on Roark\(^1\).

    $$\large{\tau _{max}}=\frac {\theta.G.r}{l} = 3.2 \ [MPa]$$

    Result Comparison

    The results obtained from SimScale for the maximum shear stress \(\tau_{max}\) at point B’ are compared with the analytical solution by [Roark].

    CaseQuantityRoarkSimScaleError (%)
    (A)Maximum shear stress \(\tau_{max} [MPa]\)3.23.209+0.289
    (B)Maximum shear stress \(\tau_{max} [MPa]\)3.23.191-0.279
    (C)Maximum shear stress \(\tau_{max} [MPa]\)3.23.195-0.152
    (D)Maximum shear stress \(\tau_{max} [MPa]\)3.23.180-0.639
    Table 3: Comparison of results at point B’.

    Inspecting the Cauchy stress magnitude for Case B in the post-processor:

    bonded contact validation cauchy stress
    Figure 4: Case B (split geometry), showing Cauchy stress magnitude contours

    References

    • W. C. YOUNG, R. G. BUDYNAS. Roark’s Formulas for Stress and Strain. Seventh Edition. McGraw-Hill. 2002. p. 415.

    Last updated: September 24th, 2021

    Contents