Documentation
Fluid flows can be classified as laminar flow and turbulent flow. Laminar flow occurs when the fluid flows in infinitesimal parallel layers with no disruption between them. In laminar flows, fluid layers slide in parallel, with no eddies, swirls or currents normal to the flow.
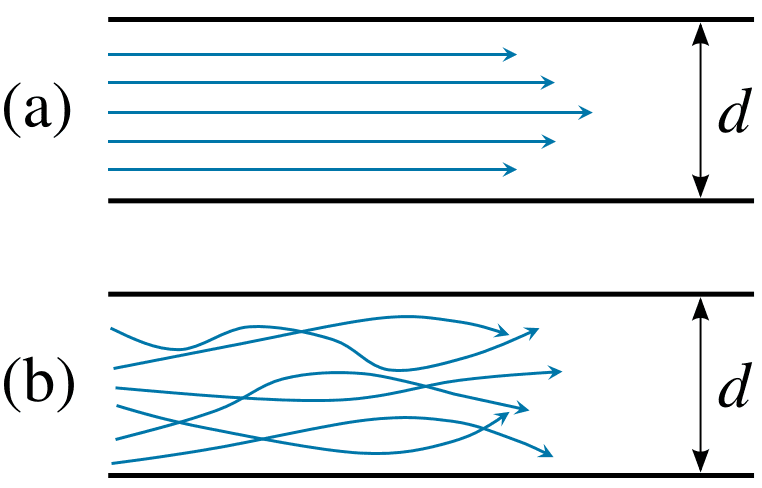
This type of flow is also referred to as streamline flow because it is characterized by non-crossing streamlines (Figure 1). That means every fluid particle follows the same trajectory of its preceding particle. Laminar flow is common when the fluid is moving slowly, through a relatively small channel, and/or with high viscosity.
The laminar regime follows momentum diffusion, while momentum convection is less important. In more physical terms, it means that viscous forces are higher than inertial forces.
The distinction between laminar and turbulent regimes was first studied and theorized by Osborne Reynolds in the second half of the 19th century. His first publication
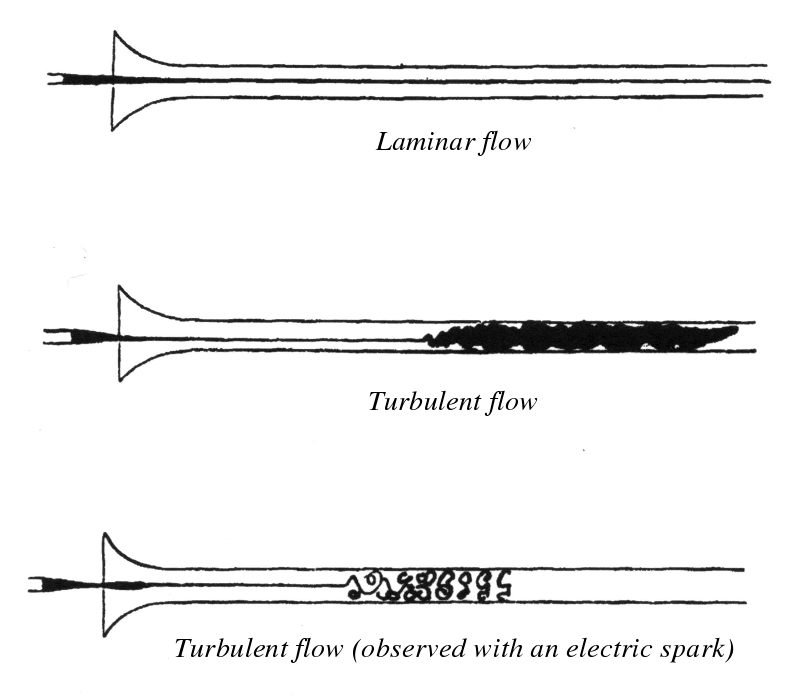
This work was based on the experiment used by Reynolds to show the transition from the laminar to the turbulent regime.
The experiment consisted of examining the behavior of water flow in a large glass pipe. In order to visualize the flow, Reynolds injected a small vein of dyed water into the flow and observed its behavior at different flow rates.
Thus, Reynolds demonstrated the existence of two different flow regimes, called laminar flow and turbulent flow, separated by a transition phase. He also identified a number of factors that affect the occurrence of this transition.
Reynolds number (Re) is a dimensionless number expressing the ratio between inertial and viscous forces. George Gabriel Stokes first introduced the concept in 1851, but Osborne Reynolds popularized it and proposed it as the parameter to identify the transition between laminar and turbulent flows. For that reason, the dimensionless number became Reynolds number, named by Arnold Sommerfeld after Osborne Reynolds in 1908
Reynolds number is a macroscopic parameter of flow in its globality and is mathematically defined as:
where:
At low values of Reynolds number, the flow is laminar. When the Reynolds number exceeds a threshold value, semi-developed turbulence occurs in the flow. This regime is usually referred to as the “transition regime” and occurs for a specific range of the Reynolds number. Beyond that range, the flow becomes fully turbulent.
The mean value of Reynolds number in the transition regime is usually named “Critical Reynolds number”. It is the threshold between the laminar and the turbulent flow.
It is interesting to notice that the Reynolds number depends both on the material properties of the fluid and the geometrical properties of the application. This has two main consequences:
The following table shows the correspondence between the Reynolds number and the regime obtained in different problems.
| Problem Configuration | Laminar regime | Transition regime | Turbulent Regime |
|---|---|---|---|
| Flow around a foil parallel to the main flow | |||
| Flow around a cylinder whose axis is perpendicular to the main flow | |||
| Flow around a sphere | |||
| Flow inside a circular-section pipe |
The transition regime separates the laminar flow from the turbulent flow. It occurs for a range of Reynolds numbers in which laminar and turbulent regimes cohabit in the same flow. This happens because the Reynolds number is a global estimator of the turbulence and does not characterize the flow locally. In fact, other parameters may affect the flow regime locally.
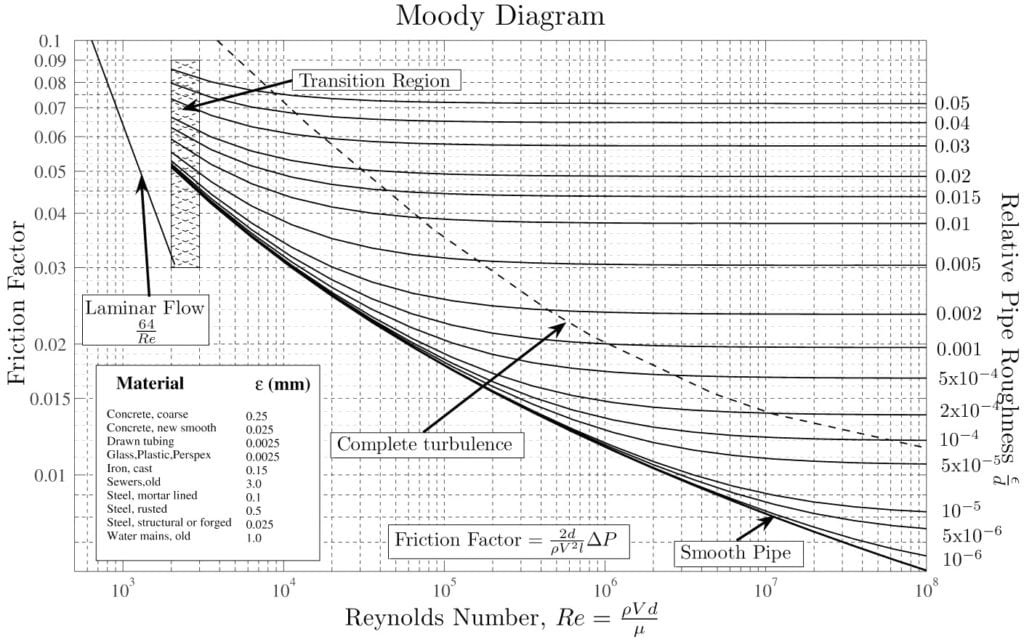
An example is a flow in a closed pipe, studied analytically through the Moody’s chart (Figure 3). The behavior of the flow (described through the friction factor) depends both on the Reynolds number and the relative roughness
Laminar flows have both academic and industrial applications.
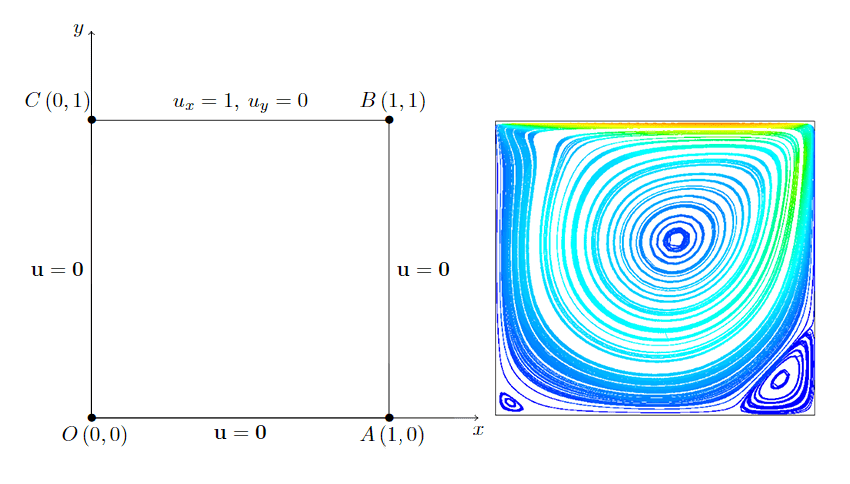
Many flows in the laminar regime are used as benchmarks for the development of advanced simulation techniques. This is the case of the “lid-driven cavity”
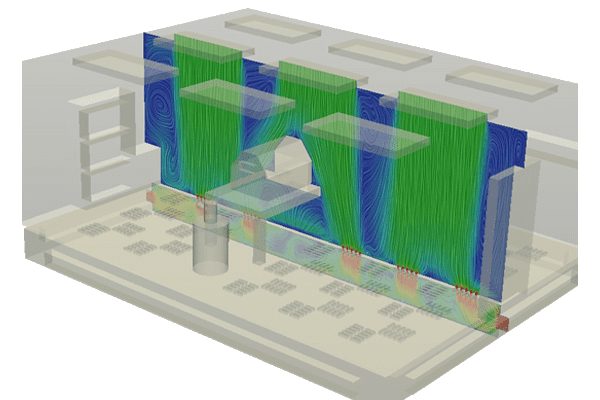
From the industrial point of view, the laminar regime is usually developed in flows with low velocity, low density or high viscosity. This is usually the case with natural convection (Figure 5) or ventilation systems working at low velocities (Figure 6).
References
Last updated: August 11th, 2023
We appreciate and value your feedback.
What's Next
What is Turbulent Flow?Sign up for SimScale
and start simulating now