Documentation
Thermophysical models define how the energy, heat, and physical properties of the fluid are calculated. These variables are then determined based on the analysis type and the selected models. The models are relations of a pressure-temperature equation system using which the required fluid properties and variables are then calculated.\(^1\)
Thermophysical fluid models can be selected under Materials after a material has been selected from the library. They are only available for compressible flow simulations. Hence, convective, conjugate heat transfer, and subsonic simulations need to have compressibility toggled on.
Important
The thermophysical models are currently applicable to Newtonian fluids only.
These settings are briefly described as follows:
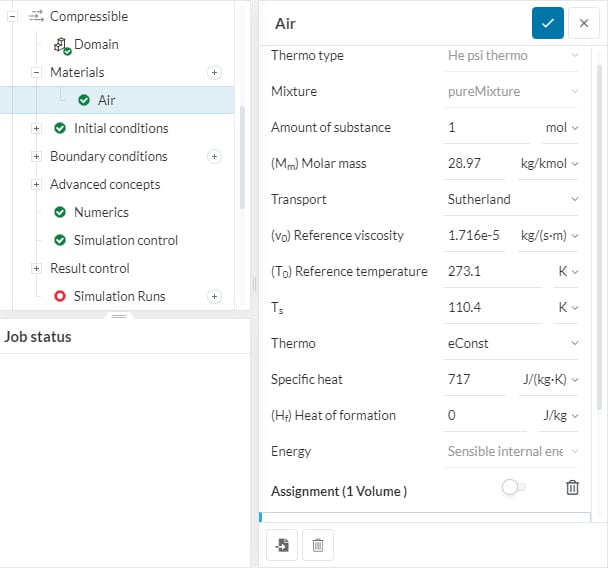
The thermo type is distinguished by the approach used to calculate the flow thermal variables. The available types on the SimScale platform are the psiThermo and rhoThermo types that are briefly detailed below:
This model is for fluids with a fixed chemical composition. It uses a variable ‘psi’, \(\psi\) that determines the compressibility as follows:
$$ \psi = \left ( RT \right )^{-1} \qquad \tag{1}$$
where \(R\) is the gas constant and \(T\) is temperature. Based on this compressibility and the changes in pressure, the density is then determined by the chosen equation of state.
Important
The He psi thermo thermo type is applicable for compressible flow analysis only
The He rho thermo type is also for fluids with fixed chemical composition. This type calculates the basic thermodynamic properties based on density variation of the fluid, \(\rho\). This is used in heat transfer analyses where the density of the fluid is changing due to changes in its temperature.
Important
The He rho thermo thermo type is applicable for convective and conjugate heat transfer analyses involving compressibility effects.
It specifies the fluid mixture composition. Generally, thermophysical models without chemical reactions are categorized as pure mixtures, which represents a mixture with fixed chemical composition. Currently, pureMixture is the only available mixture model and is selected by default.
Next, the composition of the constituents is specified. As currently, a single constituent is available, so parameter values for one constituent are required.
This is the number of moles of the component. This parameter has a default value of 1 and generally is not required to be changed.
Molar mass \((M_m)\) represents the molecular weight of the component per mole in units of \(kg/kmol\) or \(lb/kmol\) and is dependent on the molecular structure of the fluid material.
The transport model relates to the calculation of the transport variables dynamic viscosity \((\mu)\), thermal conductivity \((\kappa)\), and thermal diffusivity \((\alpha)\) for energy and enthalpy equations.\(^1\) Depending on the problem, the following types of transport models are available:
The Const type will assume a constant dynamic viscosity, \(\mu\) and Prandtl number, \(P_{r}= c_{p}\ \mu / \kappa\) . These parameters are then specified in the panel.
For the Sutherland type, the dynamic viscosity \((\mu)\) is not constant, and changes with temperature \((T)\). The dynamic viscosity is then calculated as a function of temperature given by the relation:
$$ \mu = \mu_0 \frac{T_0 + T_s}{T + T_s} \left(\frac{T}{T_0}\right)^{3/2} \tag{2}$$
where:
Referring back to Figure 1 in this documentation page, the user provides \(\mu_0\), \(T_0\), and \(T_s\) in the simulation set up. The Sutherland’s temperature (sometimes referred to Sutherland’s Constant) can be found online\(^2\) for a variety of fluids.
Thermo models are used to calculate the specific heat at constant pressure \((c_{p})\) for the fluid, from which the other properties are then derived. The following methods are available for the evaluation of \(c_{p}\).
This option assumes a constant value for specific heat at constant pressure, \(c_{p}\) and the heat of fusion, \(H_{f}\).
This option does not assume a constant value for \(c_{p}\). Rather, it assumes the specific heat at constant volume, \(c_{v}\) and the heat of fusion, \(H_{f}\) to be constant.
An equation of state is a thermodynamic relation describing the interconnection between various macroscopic properties of a fluid. In OpenFoam solver, it describes the relation between density \((\rho)\) of a fluid and the fluid pressure \((P)\) and temperature \((T)\).\(^1\)
Based on the thermophysical model type, the following equations of state can be used :
In this case, the fluid density \((\rho)\) is kept constant and does not change by pressure \((P)\) or temperature \((T)\)
$$ \rho = constant \tag{3}$$
For the case of perfect gas, the fluid is assumed to be an ideal gas and obey the ideal gas law, that is the equation of state as given by the following relation:
$$ \rho = P/(R_{specific}T) \qquad \tag{4}$$
where, \(P\) is the pressure, \(R_{specific}\) is the specific gas constant and \(T\) is the temperature.
Furthermore, the specific gas constant is given by the following equation:
$$ R_{specific} = R/M \qquad \tag{5}$$
where \(R\) is the universal gas constant, and \(M\) is the molar mass of the gas, defined under the Materials tab.
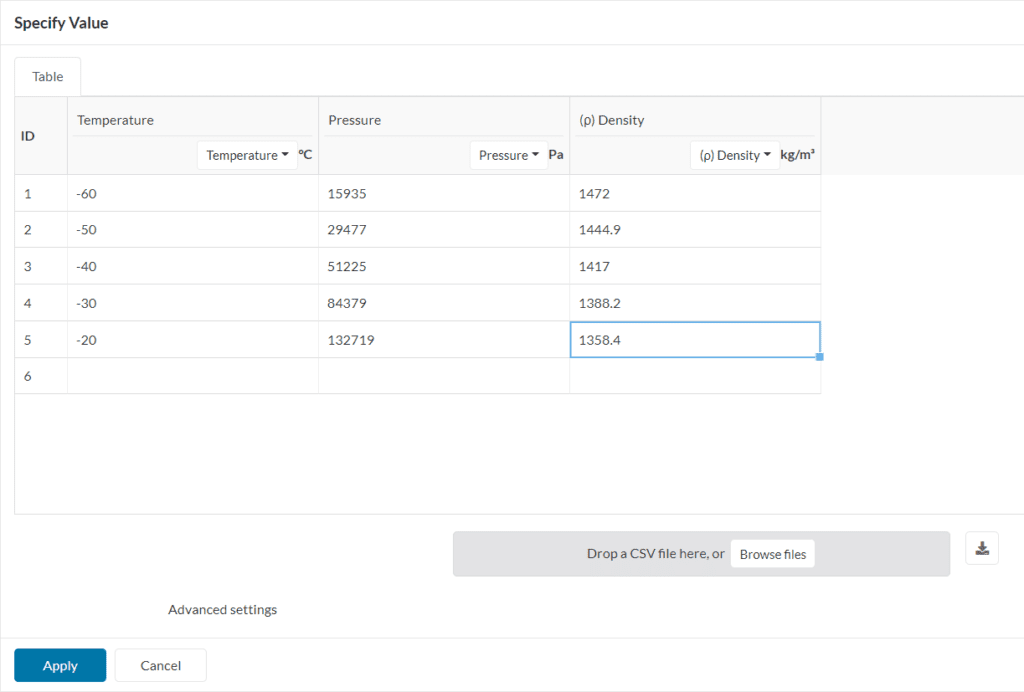
For all the cases where the fluid does not obey the ideal gas law, a generic real gas law definition can be used. This is a good option when the thermodynamic behavior of the fluid is known.
Users should be able to upload table input of thermodynamic properties like dynamic viscosity, density, and enthalpy as a function of temperature in a CSV format.
In this case, the fluid is assumed a perfect gas that is only incompressible with respect to changes in pressure, \(P\). The equation of state is then given as:
$$ \rho = P_{ref}/(R_{specific}T) \qquad \tag{6}$$
where, \(P_{ref}\) is the reference pressure, \(R_{specific}\) is the specific gas constant and \(T\) is the temperature. The specific gas constant is calculated using equation 5.
Important
For incompressible perfect gas, the gas density \((\rho)\) can vary due to changes in temperature \((T)\) .
In the perfect fluid case, the equation of state takes the form as given below:
$$ \rho=P/(RT) \ +\ \rho_{0} \qquad \tag{7}$$
where, \(\rho_{0}\) is the density at \(T = 0\). Then the density of the fluid can change both due to pressure and temperature.
Important
This option is recommended to model natural convection in liquids, e.g., water, due to changes in temperature.
Adiabatic perfect fluid follows the following equation of state:
$$ \rho = \rho_0 \left(\frac{P+B}{P_0+B}\right)^{1/\gamma} \tag{8}$$
where \(P_0\) is the reference pressure, \(B\) is offset pressure for a stiffened fluid, and \(\gamma\) is the isentropic constant.
Under Energy, two options are available for the form of energy to be used in the solution. One is the sensible internal energy and the other is sensible enthalpy. The difference between absolute and sensible energy is the absence of heat of formation in the latter.
For example, absolute enthalpy \((h)\) is related to sensible enthalpy \((h_s)\) for a single specie as follows:
$$ h=h_s+c\ \Delta h_{f} \qquad \tag{9}$$
where, \(c\) is the molar fraction and \(\Delta h_{f}\) is the heat of formation.
Important
In most cases it is recommended to use sensible enthalpy, unless energy change due to reactions is expected.
References
Last updated: October 11th, 2022
We appreciate and value your feedback.
Sign up for SimScale
and start simulating now