Modal-Based Harmonics

When performing vibration analysis, one of the important frequencies of interest is the eigenfrequencies of the part or assembly. Therefore the workflow to run a harmonics analysis requires performing a frequency analysis in advance to know these eigenfrequencies. To ease the setup SimScale allows the user to perform a modal-based analysis, within the harmonic analysis type.

To perform modal-based harmonics activate the ‘Modal-based’ solution method under the numerical settings of a harmonic simulation as shown in Figure 1.

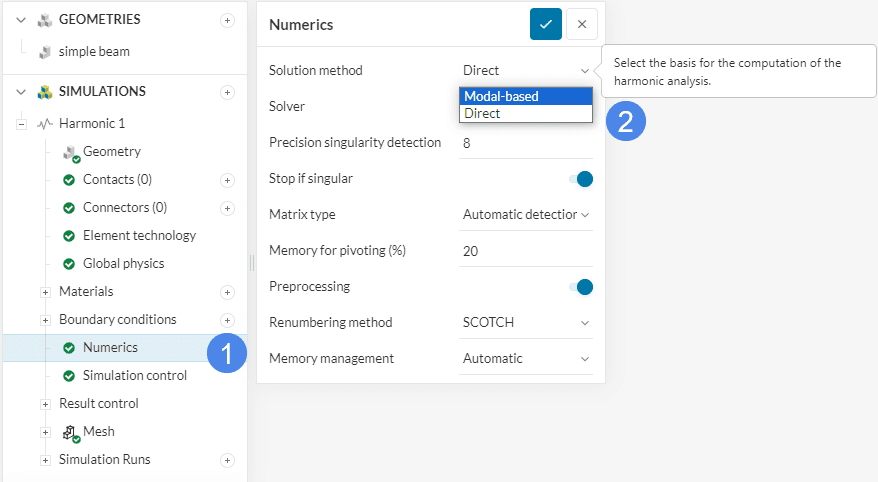
Modal based harmonics switch to modal based — Figure 1: Activate *Modal-based* harmonic solution method in the numerics section of a harmonic simulation.

Numerical Settings

Once the Modal-based option has been applied the user can adjust the numerical settings for the Modal base as well as Harmonic response.

Modal based harmonics numerics view — Figure 2: Numerics view for *Modal-based* harmonics

For more information on the numerical settings please read the following documentation:

Structural Analysis Numerics

Simulation Control

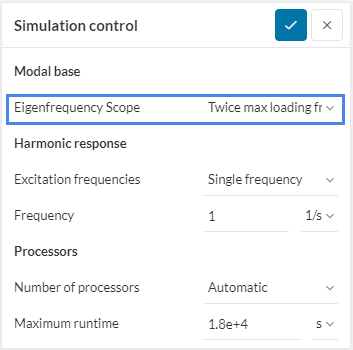
For modal-based harmonics, the eigenfrequency scope has to be defined, as well as the excitation frequency for the harmonic response. Here the setting for the harmonic response can be defined based on the eigenfrequencies of the system.

Modal base options define the method on how the eigenfrequencies should be computed. Four different options are available to find these modes.

Twice max loading frequency

This option performs a frequency analysis that covers two times the maximum frequency of the specified harmonic range, starting from 0 \(Hz\).

Modal based twice max load — Figure 3: Use twice max loading frequencies in reference to the maximum harmonic response frequency.

First Modes

The first Number of modes will be searched and computed in the order of low to high frequency.

Modal based first n modes — Figure 4: In this example, the first 10 modes will be found starting from 0 \(Hz\)

Frequency range

All the modes within the specified frequency range will be searched and computed. The frequency range is defined by a Start frequency and an End frequency.

Modal based harmonics frequenzy range — Figure 5: Compute the eigenfrequencies within the given frequency range.

Center frequency

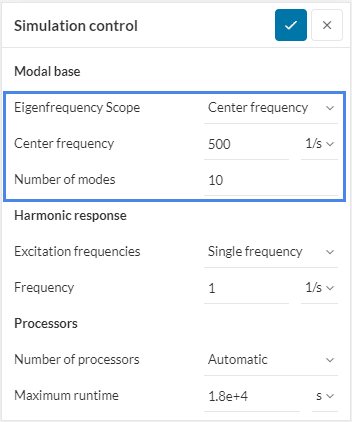
Compute the Number of modes closest to the frequency defined by the Center frequency.

Modal based center frquency — Figure 6: In this example, the first 10 eigenfrequencies will be computed that are closest to 500 \(Hz\)

Harmonic Response Options

Define the different frequencies that should be used for the harmonic simulation. The user has the option to either define a separate list of frequencies or specify the harmonic simulation based on the eigenfrequencies computed during the modal analysis.

Single frequency

Harmonic loads are applied at one frequency only.

Frequency list

Harmonic loads are applied across a range of frequencies with either a constant frequency stepping interval or a variable interval defined via a table.

Modal based harmonics hamronic frequncie list — Figure 8: Specify a frequency list for the harmonic response simulation.

Cluster around modes

Harmonic loads are applied at frequencies clustered around eigenfrequencies in the range between the start and end frequency. For each eigenfrequency within the given range, a number of frequencies within a given percentage spread.

In this example of Figure 9 five frequencies will be simulated for each eigenfrequency within the range of 1 \(Hz\) to 100 \(Hz\). The spread for these five frequencies is specified to be 10 \(\%\), which means that the spread will go from -5 \(\%\) to +5\(\%\). Within this range, the 5 frequencies are evenly spread.

Frequencies per Mode

Please note that for an even number, the eigenfrequency will still be simulated. For example, if 2 frequencies per mode are specified at a 10 \(%\) spread, three simulations will be performed. Two simulations at the spread of 5 \(%\) and one at the eigenfrequency.

Cover spectrum

Harmonic loads are applied at frequencies clustered around and in between eigenfrequencies to fully capture the entire spectrum. The user can specify a frequency range, in which the cluster around the eigenfrequencies will be computed. For each eigenfrequency within the provided range, a number of frequencies will be simulated. The first frequency will be chosen at the center between two eigenfrequencies. The distance between any further frequencies simulation is defined by the growth ratio.

Last updated: March 19th, 2024

Did this article solve your issue?

How can we do better?

We appreciate and value your feedback.