This article focuses on how to construct a mesh for multiphase analysis, and aims to answer the following questions:
- How to effectively generate a mesh for a multiphase flow analysis?
- What are the best practices for the meshing operation?
Multiphase Analysis
Before showing the best practices for the meshing of Multiphase cases, first, we need to know the peculiarities of the multiphase analysis type.
Firstly, multiphase simulations are always transient. As a result, we need to account for additional factors as we are running the meshing operation. The maximum Courant number and the timestep size are limitations that must be considered.
For stability purposes, it’s important to keep the Courant number limited to 1. From the Courant number formulation, we have:
Where
From equation 1, we can infer that using coarser cells (i.e. a larger value for
Solution
The most common mistake in the setup of multiphase analysis is to use very fine mesh cells. From the section above, we know that this results in smaller timestep sizes and ultimately makes the simulation more costly to run.
Therefore, the best practices for multiphase meshes are:
- Make sure that your CAD model is simplified, without very detailed regions. Remember that a detailed geometry takes very fine cells to mesh.
- We recommend hexahedral meshes for multiphase cases. Tetrahedral cells have difficulties to capture sharp interfaces.
- Avoid using boundary layers in the mesh. If it’s necessary to use layers, limit their number to 1.
- Keep the mesh as optimized and uniform as possible.
With these requirements, the best option for multiphase cases is the Hex-dominant (parametric) algorithm, since it gives the user full control over the cell size and refinements. Although not optimal, the Hex-dominant (automatic) algorithm can also be used, with coarse settings. Finally, the Standard meshing tool uses tetrahedral cells, therefore it is not a good option for multiphase cases.
In case you are not familiar with the hex-dominant (parametric) tool, please check this meshing tutorial.
Expected Outcome
In this section, we will show you a comparison between a standard mesh and the two versions of the hex-dominant algorithm.
The geometry is a simple tank that will be filled with water. Find below the geometry and the resulting mesh with the hex-dominant (parametric) tool:
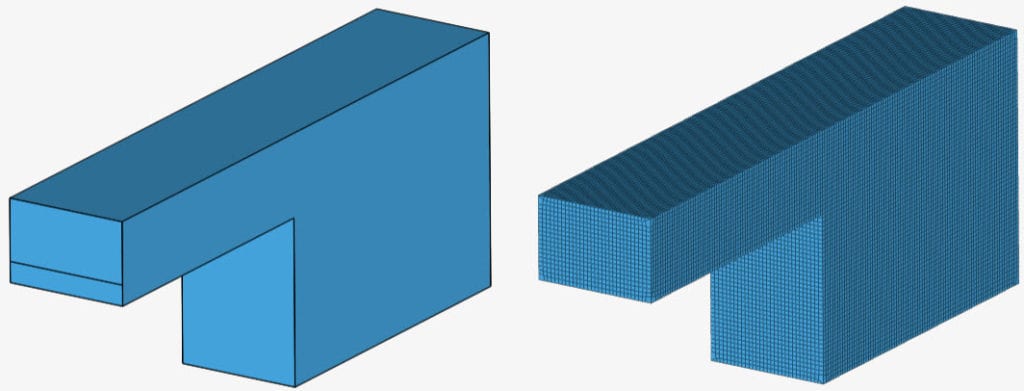
Since the user has full control over the refinements, it’s possible to craft an optimized mesh, which allows us to run a cost-effective multiphase analysis.
In Figure 2, you will find the results with the standard and the hex-dominant (automatic) algorithms.

Even though the hex-dominant automatic mesh would work for a multiphase analysis, the mesh is not optimized. Even with coarse settings, the algorithm generates small cells that will limit the timestep size. This problem is yet more visible with the standard meshing tool.
The result of a multiphase simulation with the hex-dominant (parametric) algorithm can be seen below:
Due to the construction of the mesh, the setup is much more efficient, and the water/air interface is sharp.
Note
If none of the above suggestions solved your problem, then please post the issue on our forum or contact us.