Validation Case: Rising Bubble

This validation case belongs to fluid dynamics and the aim of this test case is to validate the multiphase solver implemented in SimScale with the rising bubble case. Specifically, the following parameters are of interest:

• Bubble vertical velocity
• Bubble center of mass
• Bubble profile

The simulation results from SimScale were compared to the results presented in the study “Bubble Benchmark“\(^1\) done by TU Dortmund.

Geometry

The domain of interest is a 2-dimensional rectangular space with dimensions as below:

The width AB, CD is 1 \(m\) while the height AD, BC is 2 \(m\).

For simulation purposes, a mesh was created with the blockMesh tool in OpenFOAM® whose details can be found later in the following section.

Analysis Type and Mesh

Tool Type: OpenFOAM®

Analysis Type: Multiphase

Mesh and Element Types:

As explained before, the mesh was created with the blockMesh tool. This is a uniform mesh with only one cell-layer in the z-axis, this is done to maintain the two-dimensional flow.

Mesh Type	Number of cells	Type
snappyHexMesh	28800	2D hexahedral

Simulation Setup

Fluid:

• Case 1:
  • Gravity \((g)\) : 0.98 \(m/s^2\)
  • Surface tension \((\sigma)\): 24.5 \(N/m\)
  • Material 1:
    • Kinematic viscosity \((\nu)\): 0.01 \(m^2/s\)
    • Density \((\rho)\): 1000 \(kg/m^3\)
  • Material 2:
    • Kinematic viscosity \((\nu)\): 0.01 \(m^2/s\)
    • Density \((\rho)\): 100 \(kg/m^3\)

• Case 2
  • Gravity \((g)\) : 0.98 \(m/s^2\)
  • Surface tension \((\sigma)\): 1.96 \(N/m\)
  • Material 1:
    • Kinematic viscosity \((\nu)\): 0.01 \(m^2/s\)
    • Density \((\rho)\): 1000 \(kg/m^3\)
  • Material 2:
    • Kinematic viscosity \((\nu)\): 0.1 \(m^2/s\)
    • Density \((\rho)\): 1 \(kg/m^3\)
• The location of the bubble at t = 0 \(s\) is at y = 0.5 \(m\).

Initial and Boundary Conditions:

• Initial conditions

Only the global phase fraction was initialized and was set to the value of 1, which is the fluid surrounding the bubble.

• Boundary conditions

To simulate the rising bubble phenomenon, custom boundary conditions were used. The specific settings of the boundary conditions can be seen in the table below:

Parameter	Top and Bottom	Left and Right	Front and Back
Velocity	Fixed Value – 0 \(m/s\)	Slip	Empty 2D
Pressure	Fixed flux pressure – 0 \(Pa\)	Fixed flux pressure – 0 \(Pa\)	Empty 2D
Phase fraction	Zero gradient	Zero gradient	Empty 2D

Reference Solution

The reference solution for the center of mass and the rising velocity is given by the following equations:

$$X_c = (x_c,y_c) = \frac{\int_{\Omega_2}x\,dx}{\int_{\Omega_2}1\,dx} \tag{1}$$

$$U_c = \frac{\int_{\Omega_2}u\,dx}{\int_{\Omega_2}1\,dx} \tag{2}$$

where:

• \(X_c\): x- and y-coordinates of the center of the bubble
• \(\Omega_2\): the region the bubble resides\(^1\)
• \(U_c\): rising velocity of the bubble
• \(u\): velocity of the center of the bubble

Result Comparison

The comparison for the center of mass and the rising velocity of the bubble obtained from SimScale against the reference results obtained from the “Bubble Benchmark“\(^1\) is shown in figures below:

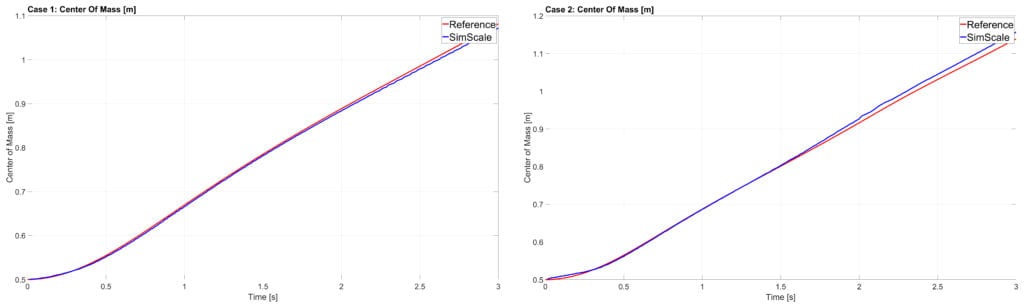
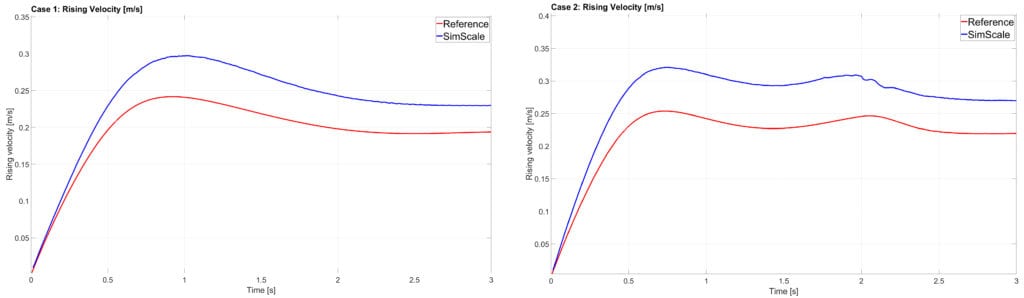
The movement of the bubble for each case can be seen in the animation below:

Last updated: October 23rd, 2020