Large Eddy Simulation: Flow Over a Cylinder

The purpose of this numerical simulation is to validate the following parameters of the incompressible Large Eddy Simulation (LES) flow over a cylinder:

• Pressure distribution on the cylinder surface
• Stream-wise Velocity distribution in the wake

The numerical simulation results of SimScale were compared with the experimental results\(^{1,2,3}\). The flow regime selected for the study is classified as sub-critical with a flow Reynolds number of \(Re\)=3900.

Geometry

The geometry of the study is a straight cylindrical body (see Figure 1). A brief description of the dimensions is provided by the table below.

An O-type domain is selected as the flow domain around the cylinder. For cylinder diameter \(D\), the domain is 15 \(D\) in the radial direction and \(\pi D\) in the span-wise direction (see Figure 2). 

Dimensions are given below

Dimension	Value \([m]\)
Cylinder Diameter	0.1
Domain Thickness	0.314
Domain Diameter	3

Analysis Type and Mesh

Tool Type: OpenFOAM®

Analysis Type: Transient, Incompressible with LES Smagorinsky turbulence model.

Mesh and Element Types:

For this study, a structured hexahedral mesh was created with the open-source ‘BlockMesh-tool’. The grid nodes are distributed by a geometric grading in the radial direction. Further, the nodes are clustered near the stagnation point and in the wake region along the streamwise direction. The mesh is based on a y-plus \((y+)\) criterion of \(y+\)<1 in the radial direction. The complete details of the mesh are listed in Table 2:

Simulation Setup

Fluid:

• \((\nu)\) Kinematic viscosity: 0.0000151116 \(m^2/s\)
• \((\rho)\) Density: 1 \(kg/ m^3\)

Boundary Conditions:

The inlet boundary was set as a non-turbulent fixed velocity condition, while a pressure boundary condition was applied at the outlet. For the spanwise boundaries, a symmetry condition was applied. The following table provides further details.

Boundary Surface	Velocity	Pressure
Inlet	Fixed value of 0.59 \(m/s\)	Zero gradient
Outlet	Inlet-outlet	0 \(Pa\) Fixed value gauge pressure
Cylinder Wall	Fixed value of 0 \(m/s\)	Zero gradient
Front and back faces	Symmetry	Symmetry

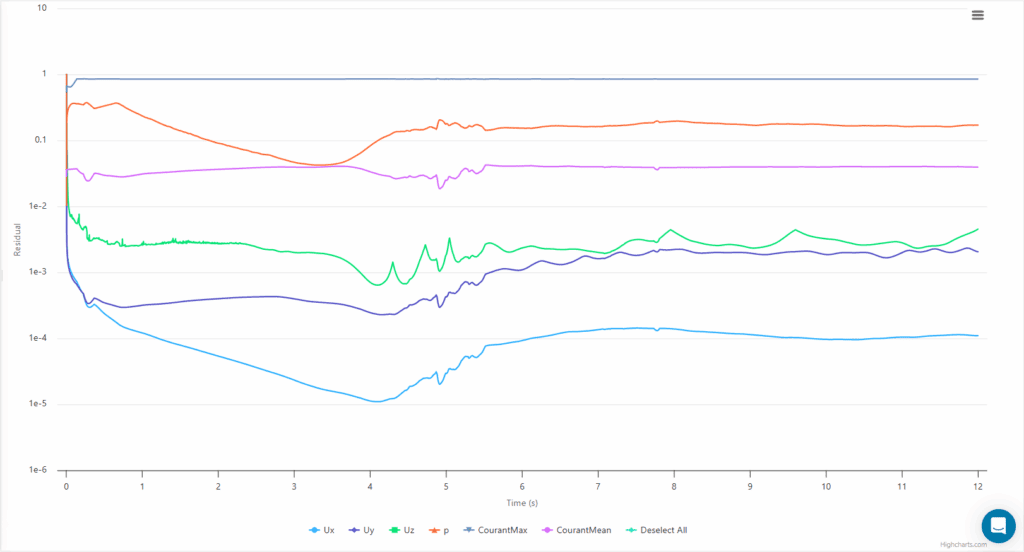
To ensure meaningful results, it was ensured that the simulation was run for at least 3 fluid passes. The distance from the cylinder to the outlet is 1.5 \(m\). Thus, for the 0.59 \(m/s\) inlet velocity, 3 fluid passes would take approximately 8 seconds. The simulation was run for 12 seconds to achieve trustworthy results.

Result Comparison

The convergence plots seem to find an acceptable stability after 7 seconds. Since this is a transient simulation with eddies resolved, it was important to find the mean value of the comparing variables over the final few time steps (8-12 seconds).

The mean stream-wise velocity profile was calculated by averaging the x-component of the velocity at time steps 8, 9, 10, 11, and 12 seconds. This is compared with experimental data provided by L.Ong and J.Wallace\(^2\), and L.M.Lourenco and C.Shih\(^3\) as shown in Figure 4.

A comparison of the mean pressure distribution obtained with SimScale and experimental data provided by C.Norberg\(^1\) is given in Figure 5.

A visualization of the instantaneous flow field for the velocity and pressure fields of the LES cylinder validation case is shown in Figures 6 to 10, along the cross-sectional and spanwise planes, at a time step of 9 seconds.

Last updated: July 18th, 2025