Tutorial: Nonlinear Structural Analysis of a Wheel

This article provides a step-by-step tutorial for the nonlinear structural analysis of a wheel. The objective of this simulation is to analyze the deformation and stress distribution across the wheel in operation mode, taking into account the nonlinear phenomena such as hyperelastic material, physical contact, and alternating load.

This tutorial teaches how to:

• Set up and run a nonlinear structural analysis.
• Assign boundary conditions, materials, and other models to the simulation.
• Mesh the geometry with SimScale’s standard meshing algorithm.
• Explore the results using SimScale’s online post-processor.

The typical SimScale workflow will be followed:

1. Prepare the CAD model for the simulation.
2. Set up the simulation.
3. Create the mesh.
4. Run the simulation.
5. Analyze the results.

1. Prepare the CAD Model and Select Analysis Type

To start, you can import a copy of the project into your workbench to follow along the steps by clicking the button below:

The following picture shows what should be visible after importing the tutorial project. You can find the geometry Wheel and its 3D model displayed in the Workbench. You can interact with the model as with any CAD program by rotating, zooming, and panning.

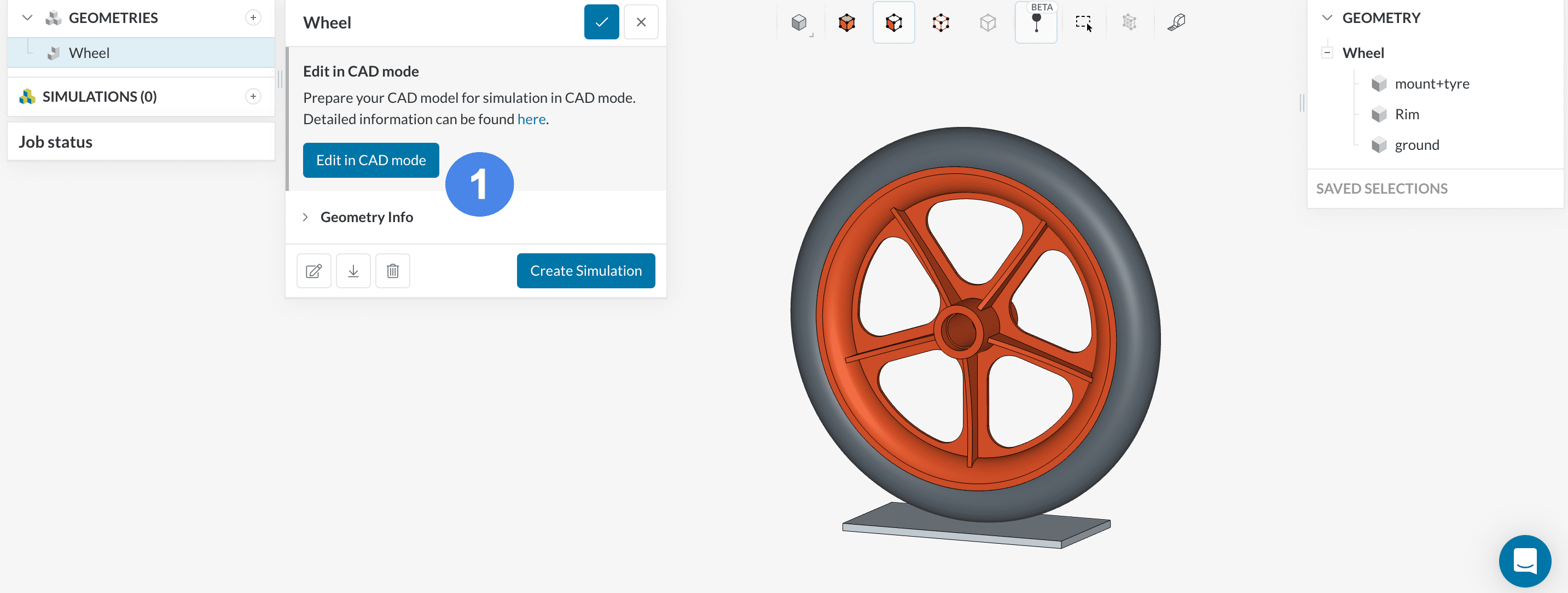
This simulation leverages the double symmetry of the model, with two goals:

1. Save on computational resources
2. Be able to restrict the model from rigid body motions in the X and Y directions, making it more stable.

It is always advisable to take advantage of symmetrical models in simulations. In order to extract the symmetrical model, we will use the CAD Edit Mode. For this, click the ‘Edit in CAD mode’ button (1 in figure 2) from the geometry pop-up. The CAD mode is opened for this geometry.

In order to extract the symmetrical model, we use the Split operation:

1. Select the ‘MODEL’ > ‘Split’ operation from the toolbar.
2. Make sure that the orientation is ‘Y’.
3. Click ‘Apply’.

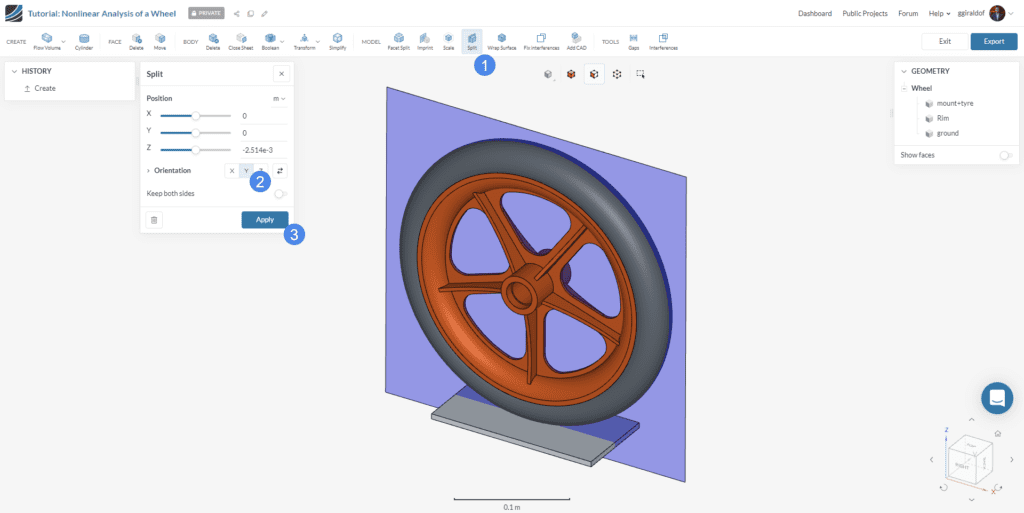
This process will result in the halved model being extracted. Now you can repeat the process to extract the quarter symmetrical model, just changing the orientation from ‘Y’ to ‘X’ in step 2. You should end up with the following geometry:

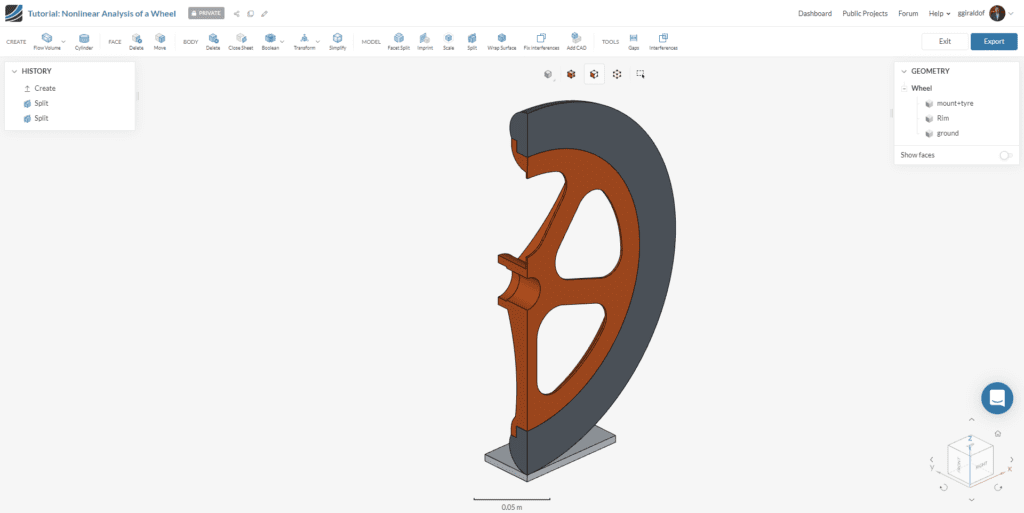
Finally, click ‘Export’ at the top right to save the changes and import the modified model to the Workbench for simulation. You can change the name of the new geometry named Copy of Wheel for something more meaningful, like Wheel-Quarter:

1.1 Create a Nonlinear Structural Analysis

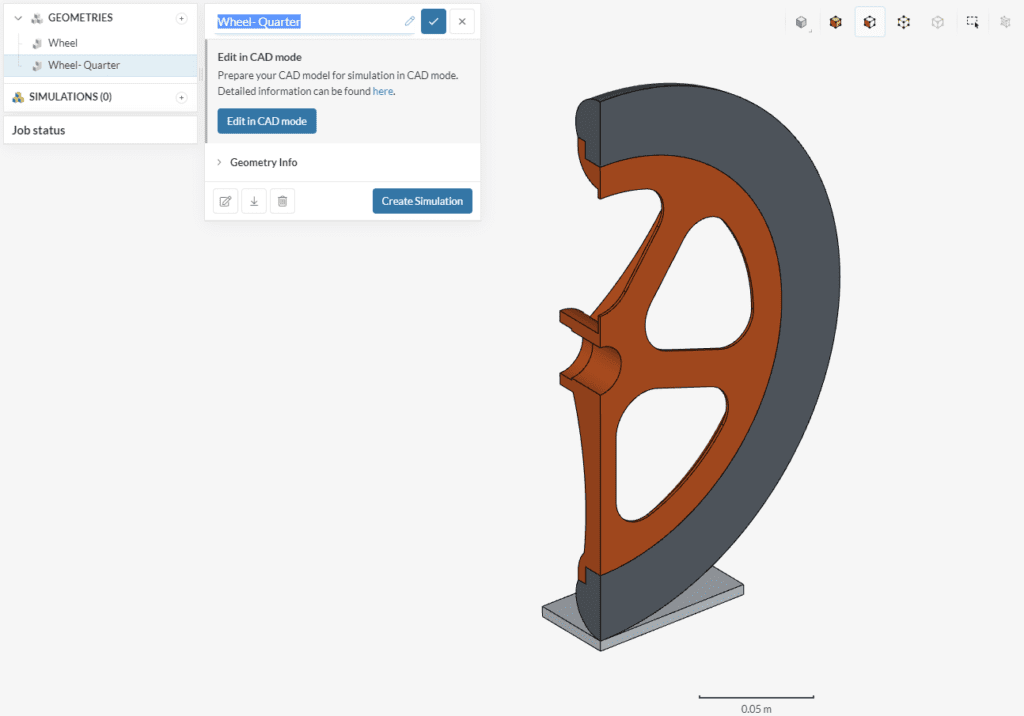
Now the simulation setup can be started. Follow these steps to create a new simulation:

1. Select the ‘Wheel-Quarter’ geometry in the left panel.
2. Click the ‘Create Simulation’ button in the pop-up window.

The simulation library window appears. Select the ‘Static‘ analysis type and click the blue ‘Create Simulation’ button at the bottom:

As this structural simulation will include nonlinearities such as physical contact, hyperelastic materials, and varying load, the nonlinear analysis type must be activated. In the global settings panel that is opened after creating the simulation, activate the Nonlinear analysis toggle:

Now a new simulation tree will be automatically generated in the left panel containing all the parameters and settings that are necessary to completely specify the analysis. All the portions of the setup that are completed are highlighted with a green check. On the other hand, the portions that need to be specified have a red circle. A blue circle indicates an optional setting that is not mandatory. Check the following figure for illustration:

You can find more details about what characterizes a static analysis here.

2. Set Up the Nonlinear Structural Analysis

The analysis of the wheel will include the following operating conditions:

1. The wheel rim is made out of polypropylene material.
2. The wheel tyre is made out of rubber, with big deformations expected to occur.
3. Maximum operating load of 1000 \(N\).
4. Mean operating load of 500 \(N\).
5. The tyre-ground pair must model the physical contact.

The following picture summarizes the nonlinear modeling conditions:

2.1 Contacts

Two contact conditions will be specified:

1. Interface between rim and tyre: A linear bonded contact is specified to get compliant deformation.
2. Interface between ground and tyre: A nonlinear physical contact is specified to get realistic behavior.

The bonded contact (1) is automatically detected and created by SimScale. It can be found under the Contact items under the simulation tree as Bonded 1:

Now, physical contact (2) is created. Follow the instructions shown in the picture:

1. Click the ‘+’ icon next to Physical contacts and select Physical contact from the menu.
2. Change the Contact stiffness to High.
3. Click on the Master assignment box, then select the corresponding face from the ground part.
4. Click on the Slave assignment box, then select the corresponding face from the tyre.

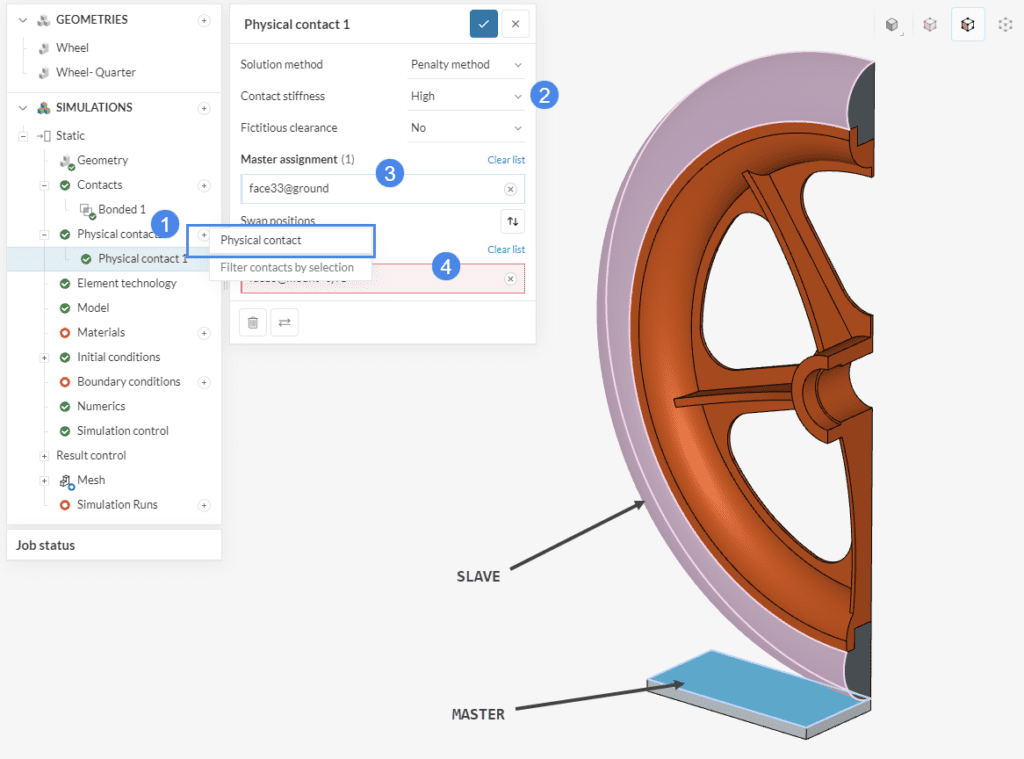
Click the check mark to finish the setup.

The selection of faces to be assigned the master/slave is performed according to the key concepts explained in the following article.

this article.

Which Surface Should I Select as the Master in a Contact Pair?

2.2 Material Model

Next, add the material models from the material library. For this, we start by clicking the ‘+’ button next to the Materials node in the simulation tree. This opens a material library from which we select the adequate material and click on the ‘Apply’ button. This will then load the standard properties for the selected material.

In the settings panel, the target body that will have the material properties applied is assigned. Accept the selection with the blue checkmark .

Use these instructions to assign the following material to each body in the CAD model:

A. Ground

For the ground body, select the Concrete material from the material library, and assign the ground body (selected from the viewer or the Scene tree on the right), as shown in the picture:

B. Rim

For the wheel rim, select the PP (polypropylene) material from the material library, and assign the Rim body, as shown in the picture:

C. Tyre

For the wheel tyre, select the Rubber material from the material library, and assign the mount+tyre body. As this body is so soft and will undergo large deformations due to the load and the physical contact with the ground, a hyperelastic material model is specified. Change the Material behavior to Hyperelastic, and set up the parameters as shown in the picture:

The input values are:

• Hyperelastic model: Mooney-Rivlin
• \(C_{10} = \) 7.36e6 \(Pa\)
• \(C_{01} = \) 1.84e6 \(Pa\)
• \(D_{1} = \) 1e-4 \(1/Pa\)
• \(\rho = \) 930 \(kg/m^3\)

2.3 Boundary Conditions

Now, we define the boundary conditions. To create a boundary condition, click on the ‘+’ button next to the Boundary conditions node in the simulation tree, and select the required boundary condition type from the drop-down menu, as shown in Figure 15.

A. Ground Fixed Support

Our first boundary condition will be to fix the ground. Select the Fixed support boundary condition from the boundary conditions drop-down menu. Assign the ground body by first activating Assign Volume from the top bar, as shown on figure 16. Give an appropriate name to the boundary condition, such as ‘Fixed support ground’.

B. Symmetry Plane Normal to X

The second boundary condition specifies the restricted normal displacement in the symmetry plane through which the model was cut. Select a Symmetry plane boundary condition and assign all the faces belonging to the symmetry plane as shown in the picture:

C. Symmetry Plane Normal to Y

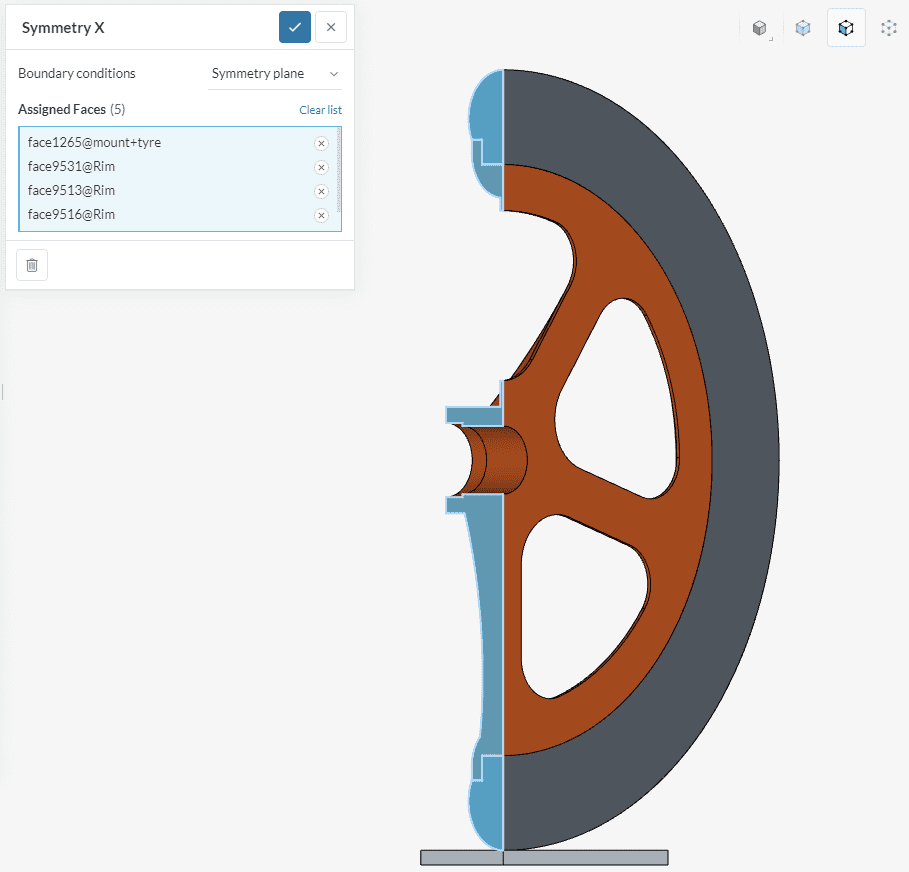
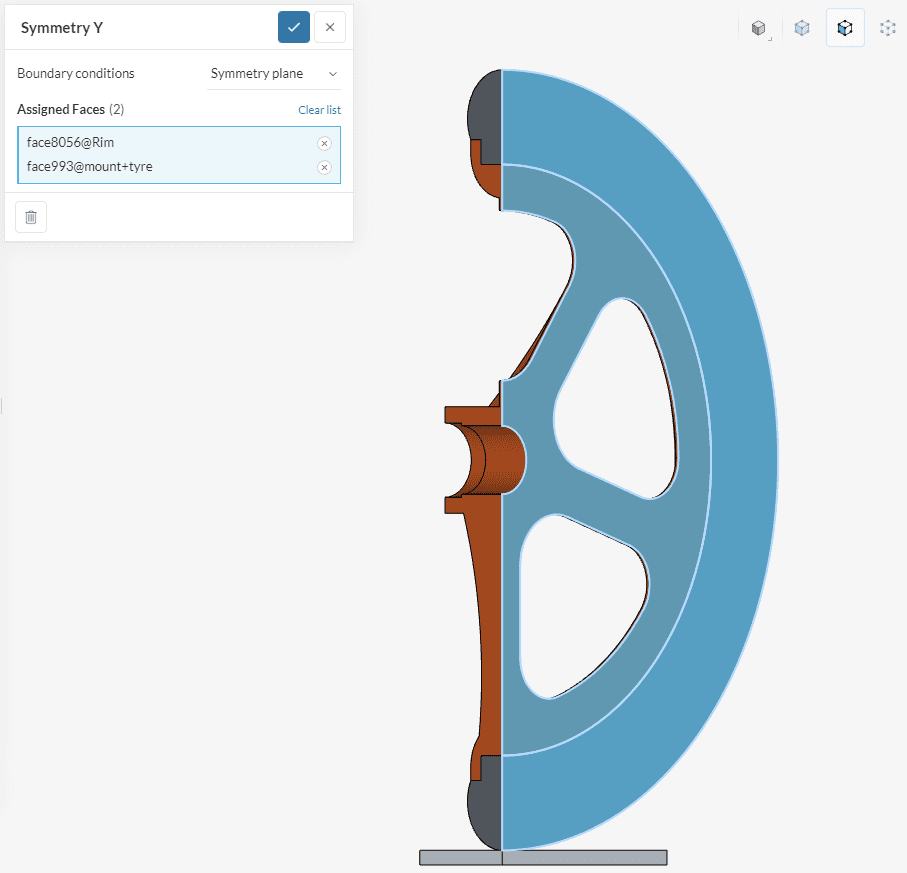
Use the same procedure as before to specify the second symmetry plane. Set up the condition as shown in the picture, assigning the corresponding faces:

D. Load

For the operating load supported by the wheel, select a Force boundary condition. Assign the central cylindrical faces as shown in Figure 10. Then, click the varying load icon as shown in the picture:

The Specify value window will appear for us to input the load curve. In this case, we will use a table input, with the setup as shown in the picture:

t \([s]\)	Fx \([N]\)	Fy \([N]\)	Fz \([N]\)
0	0	0	0
0.5	0	0	-1000
1.0	0	0	-500

Notice that our load force starts at zero, maxes out at \(t = 0.5\ s\) and then goes back down to the mean value at \(t = 1.0\ s\). The negative value indicates the force direction with respect to the Z axis. The load curve can be visualized in the following plot:

3. Numerics and Simulation Control

The Numerics section of the simulation tree can be left with the default values, as they are good enough to solve this case. In most cases, you will not have the need to modify these parameters, due to the carefully tuned default parameters.

For Simulation Control you also do not need to change any parameter. As we assumed the simulation interval to be the default value of 0 to 1, we can proceed without needing to touch this section.

4. Mesh Setup

In order to achieve optimal results, we are going to build a structured mesh using the Standard meshing algorithm. Select the mesh option and check the default settings, which will not be changed. Also, you do not need to click the Generate button at this step, as the mesh will be computed as part of the simulation run.

We will use mesh refinements to achieve the structured mesh. To create a mesh refinement, simply click the ‘+’ button next to Refinements below Mesh and select the type of refinement that you wish to create:

4.1 Swept Mesh for the Ground

For the first refinement, select a Sweep meshing refinement. This allows us to specify a structured mesh that can produce hexahedral and prismatic elements, which have the best numerical performance than the unstructured tetrahedrons.

Select opposite faces, that are connected one-to-one on their vertices to have a valid sweep, as shown in the figure:

1. Set the Sweep sizing type to ‘Number of elements along sweep’.
2. Set the Number of elements to ‘3’.
3. Set the Surface element type to Quad dominant.
4. Toggle on the Specify start/end mesh size.
5. Set the Maximum edge length to ‘0.02’ \(m\).
6. Select the Start faces box, then assign the top face of the ground.
7. Select the End faces box, then assign the bottom face of the ground.

4.2 Swept Mesh for the Tyre

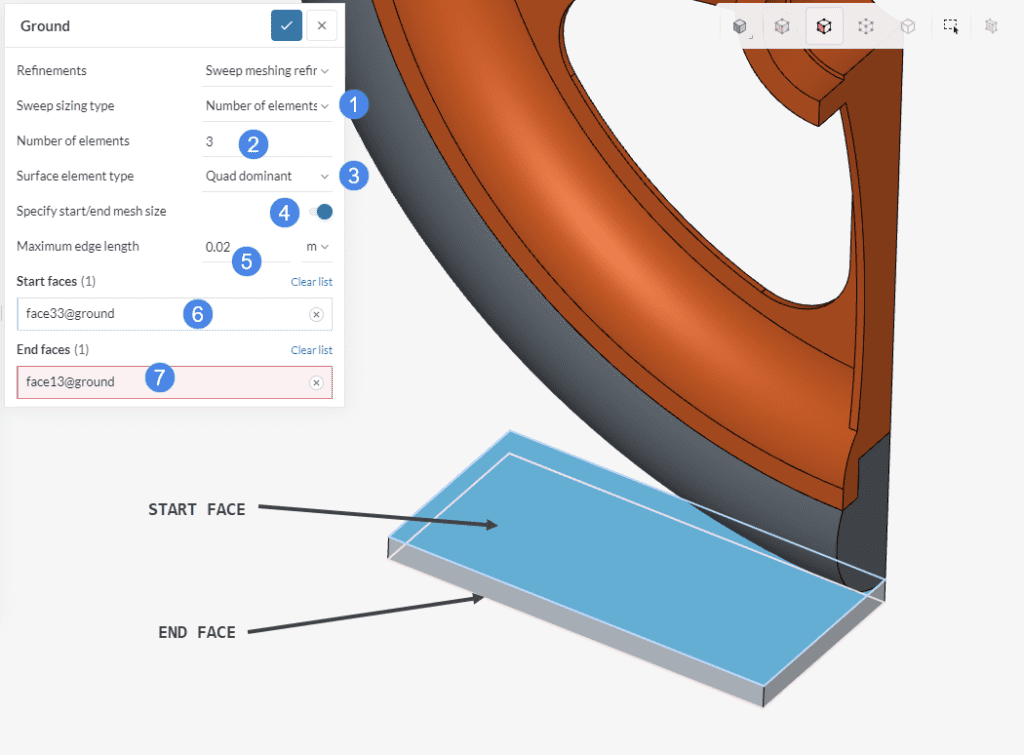
We can also leverage the prismatic shape of the tyre to create a structured mesh for this part. Create a second Sweep meshing refinement and set it up as indicated:

1. Set the Sweep sizing type to Number of elements along sweep.
2. Set the Number of elements to ’40’.
3. Set the Surface element type to ‘Quad dominant’.
4. Toggle on the Specify start/end mesh size.
5. Set the Maximum edge length to 0.002 \(m\).
6. Select the Start faces box, then assign the shown face.
7. Select the End faces box, then assign the shown face.

4.3 Region Refinement for the Rim

Finally, as the rim part mandates an unstructured mesh, we will limit the element edge length to achieve the maximum quality in terms of aspect ratio. Create a Region refinement, and set up as follows:

1. Set the Maximum edge length to ‘0.002’ \(m\).
2. Assign the Rim to the refinement.

5. Start the Simulation

The last thing to do for running this simulation is to create a run. The new run is created by clicking on the ‘+’ button next to Simulation Runs:

In the pop-up window, you can give a meaningful name to the run, then click the ‘Start’ button to launch the computation.

The Job status item below the simulation tree updates the status of the run. Also, a Solver log is provided after a few seconds which shows the advancements of the actual computing algorithm. The simulation run should take a few minutes to be carried out. Once the simulation run is Finished, we can post-process the results.

6. Post-Processing

Once the simulation is finished, you can post-process the wheel load results on the platform in one of two ways:

1. Click the ‘Post-process results’ button in the simulation run dialog, or
2. Click ‘Solution Fields’ under the simulation run tree item.

6.1 Visualizing Stress

In order to examine the stress results on the wheel, we should select the field assigned to the Parts Color as ‘Von Mises Stress’:

The parts are now colored according to the levels of stress, but we will perform some tweaking to better visualize the results:

1. Change the time step to ‘0.5 \(s\)’, which corresponds to the point of maximum loading.
2. Change the stress units to ‘\(MPa\)’.
3. Right-click on the legend bar and select ‘Use continuous scale’ from the contextual menu.

You should end up with the following visualization:

Figure 32 shows the stress distribution on the model of the wheel at the time of maximum load. It can be seen that maximum stress levels of around 41.3 \(MPa\) occur at the rim radius element and at the contact patch between the tire and the ground.

6.2 Deformed Shape

1. In the Parts Color panel, select the ‘Displacement Magnitude’ as Coloring.
2. Right-click on the legend bar and select ‘Use continuous scale’ from the contextual menu.

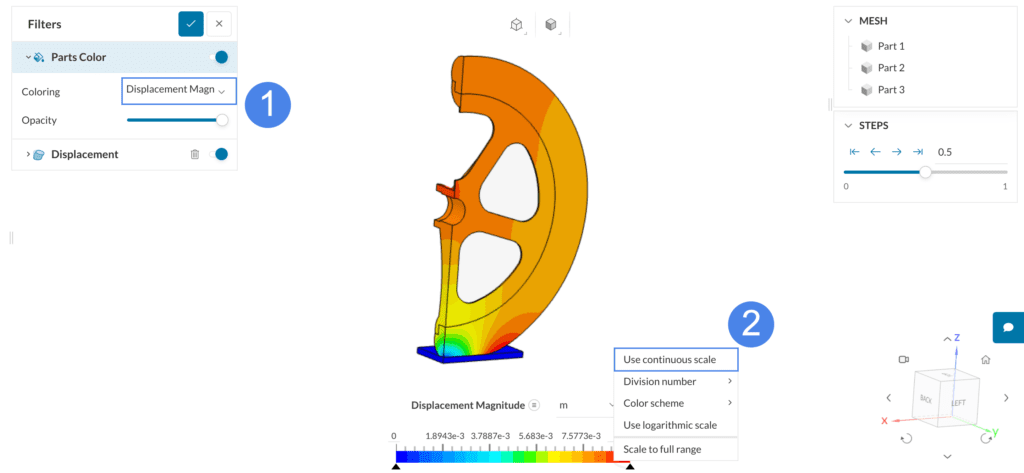
In order to visualize the deformed shape of the wheel, create a Displacement plot:

The deformed shape along with the coloring can then be inspected:

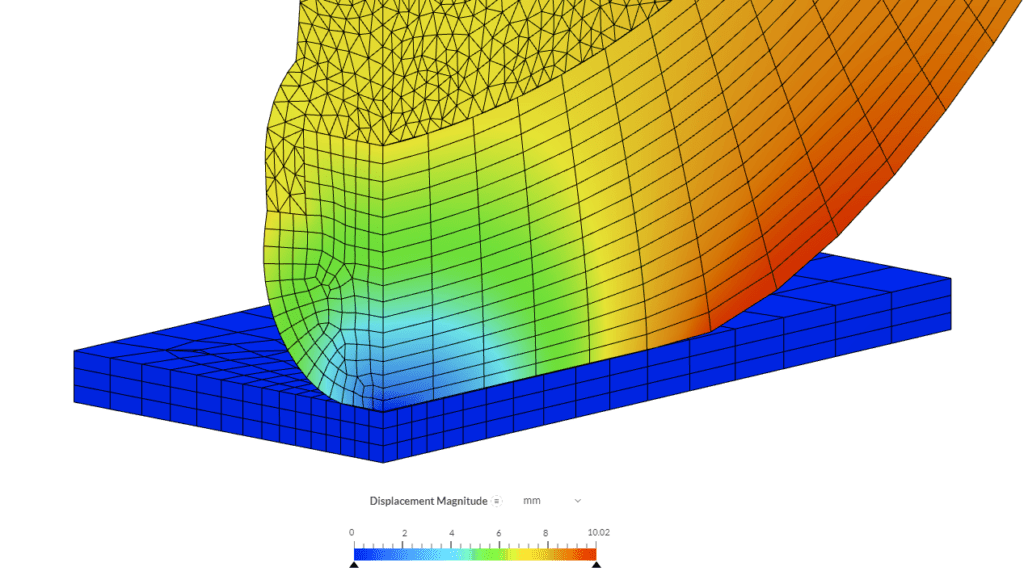
The details of the deformation of the tyre in the region of contact with the ground is well appreciated.

6.3 Animation of the Results

We can visualize the loading and unloading process and the evolution of the deformation by creating an Animation filter, the same way we added the Displacement filter (see Figure 34):

The default parameters are enough for our purpose. Click the ‘Play’ button to start the animation and you should see something as shown:

Animation 1 shows the deformation process and the corresponding contour plot for the von Mises stress. The effect of the load curve and the points of maximum deformation and stress can be appreciated.

Finally, we can take a look at the load vs. deformation plot, created locally by measuring the displacement of a point at the center of the wheel in post-processing tool Paraview, and using the known force curve:

Figure 37 shows the vertical displacement magnitude of a point at the load application face, versus the applied load magnitude. Here, the nonlinear behavior of the model can be clearly seen, with the curvature of the load vs displacement curve following the hyperelastic behavior on the loading and unloading steps.

If you want to learn more about SimScale’s online post-processor, you can have a look at our dedicated guide:

Integrated Post-Processor

Congratulations, you finished the differential casing tutorial!

Last updated: September 28th, 2023