Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

Documentation

SimScale DocumentationValidation CasesValidation Case: Taylor-Couette Flow

Validation Case: Taylor-Couette Flow

The Taylor-Couette flow validation case belongs to fluid dynamics. This test case aims to validate the following parameters:

  • Rotating wall
  • Velocity profile
  • Pressure profile

SimScale’s simulation results were compared to analytical results obtained from methods elucidated in the Scholarpedia article on Taylor-Couette flow\(^1\).

View Project

Geometry

The so-called Taylor-Couette flow occurs in the gap between two infinitely long concentric cylinders, when at least one of them is rotating. Therefore, the geometry for this project consists of a slice of an annulus between two cylinders, as seen in Figure 1:

taylor-couette flow geometry
Figure 1: Annulus between two concentric cylinders, used to study the Taylor-Couette flow.

The dimensions of the geometry are given in Table 1:

Geometry parametersDimension \([m]\)
Outer radius (a)1
Inner radius (b)0.35
Thickness of the slice (c)0.1
Table 1: Dimensions of the concentric cylinders.

Analysis Type and Mesh

Tool Type: OPENFOAM®

Analysis Type: Steady-state incompressible flow

Turbulence Model: Laminar

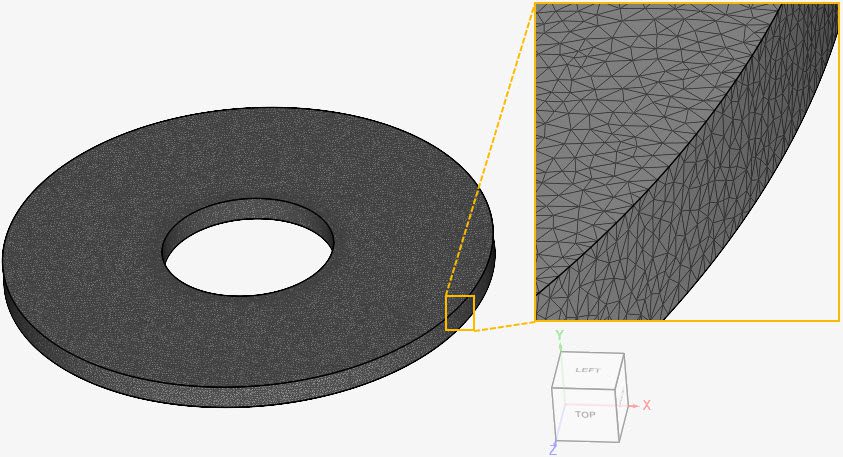
Mesh and Element Types: The mesh used in this case was created in SimScale with the standard algorithm.

Find in Table 2 an overview of the resulting mesh:

CaseMesh TypeCellsElement Type
Taylor-Couette flowStandard4884573D tetrahedral/hexahedral
Table 2: Standard mesh characteristics. The mesh consists of tetrahedral and hexahedral elements.

Find below the standard mesh used for this case:

standard mesh validation case taylor couette
Figure 2: Standard mesh, with region refinements applied to the area around the inner cylinder wall.

Simulation Setup

Material:

  • Viscosity model: Newtonian;
  • \((\nu)\) Kinematic viscosity: 1e-5 \(m²/s\);
  • \((\rho)\) Density: 1 \(kg/m^3\).

Boundary Conditions:

Before defining the boundary conditions, the current nomenclature will be used for the rest of this documentation:

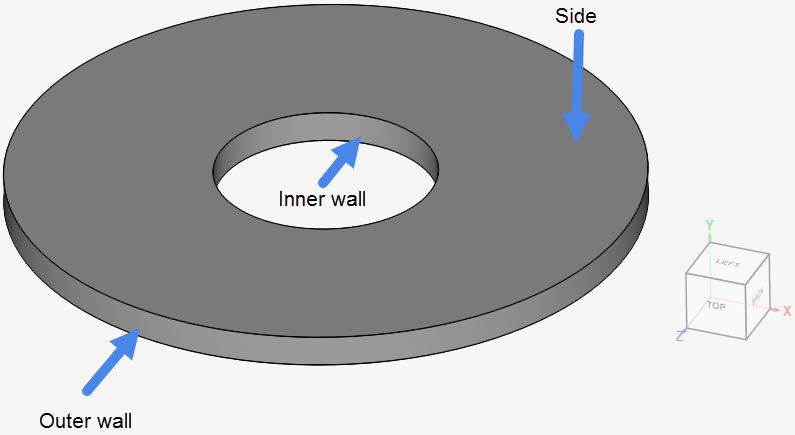
identification of patches for boundary conditions taylor-couette flow
Figure 3: Nomenclature for the assignment of boundary conditions.

In the table below, the configuration for both velocity and pressure are given at each of the boundaries:

NomenclatureBoundary TypeVelocityPressure
Inner wallCustomRotating wall: 0.001 \(rad/s\) around the positive y-axisZero gradient
Outer wallCustomFixed value: 0 (no-slip condition)Zero gradient
SidesCustomSymmetrySymmetry
Table 3: Summary of the boundary conditions used for all cases

Reference Solution

The analytical solution\(^1\) for Taylor-Couette flow is computed from the simplified Navier-Stokes in cylindrical coordinates. Before calculating the velocity and pressure profiles, we need to calculate two constants, \(A\) and \(B\):

$$A = \frac {\omega_{out}R_{out}^2-\omega_{in}R_{in}^2}{R_{out}^2-R_{in}^2} \tag {1}$$

$$B = (\omega_{in} – \omega_{out})R_{out}^2\frac {R_{in}^2}{R_{out}^2-R_{in}^2} \tag{2}$$

where:

  • \(\omega_{in}\) and \(\omega_{out}\) \([rad/s]\) are the rotational velocities of the inner and outer walls, respectively;
  • \(R_{in}\) and \(R_{out}\) \([m]\) are the inner and outer walls’ radius.

The resulting velocity profile \(U\) is a function of radius \(r\). The equation is given below:

$$U(r) = Ar + \frac {B}{r} \tag {3}$$

Similarly, for pressure \(P\):

$$P(r) = A^2\frac {r^2}{2}+2ABln(r)-\frac {B^2}{2r^2} \tag {4}$$

Result Comparison

The velocity and pressure variation in the radial direction obtained with SimScale are compared to the analytical solution.

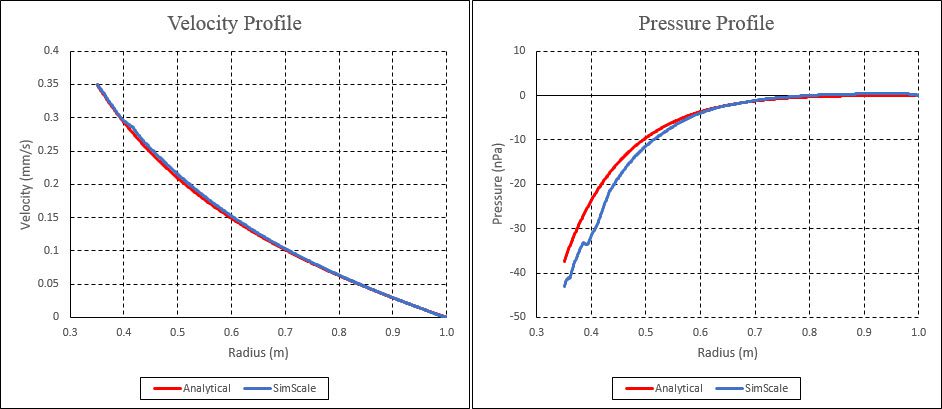
pressure and velocity profiles taylor-couette flow
Figure 4: Result comparison between SimScale’s results and the analytical solution, for velocity and pressure.

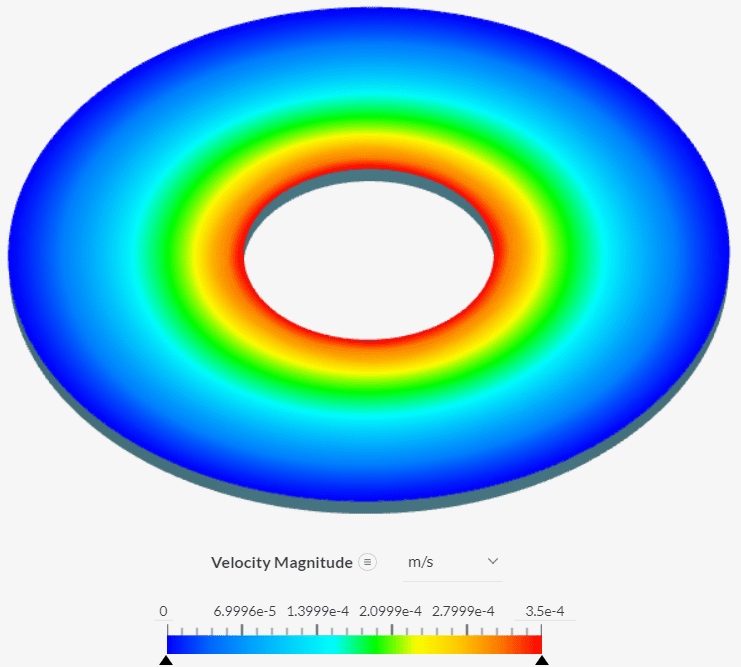
In Figure 5, we can see the velocity profile due to the rotation of the inner wall.

velocity contours taylor-couette flow
Figure 5: Velocity magnitude contours obtained in the present validation case with the standard mesher.

References

Last updated: June 23rd, 2021

Contents