Validation Case: Compressible Flow In a de Laval Nozzle

This validation case belongs to fluid dynamics. The aim of this test is to validate the following parameters for a compressible, steady-state turbulent flow through a de Laval Nozzle:

• Mach number across the nozzle.
• Pressure across the nozzle.

The simulation results from SimScale were compared to analytical results obtained from methods presented in [1].

Geometry

A typical configuration of the de Laval nozzle with a non-smooth throat that was chosen as the geometry can be seen below:

The nozzle is axisymmetric and an angular slice of the complete geometry with a wedge angle of 18$°$ was used. The following table contains the coordinates of the reference points:

Point	$x$ $[mm]$	$y$ $[mm]$	$z$ $[mm]$
A	0	0	0
B	0	5.5434	35
C	0	-5.5434	35
D	68.68	0	0
E	68.68	3.1677	20
F	68.68	-3.1677	20
G	238.8	6.3354	40
H	238.8	0	0
I	238.8	-6.3354	40

Analysis Type and Mesh

Tool Type: OpenFOAM®

Analysis type: Compressible with the k-omega SST turbulence model

Time dependency: Steady state

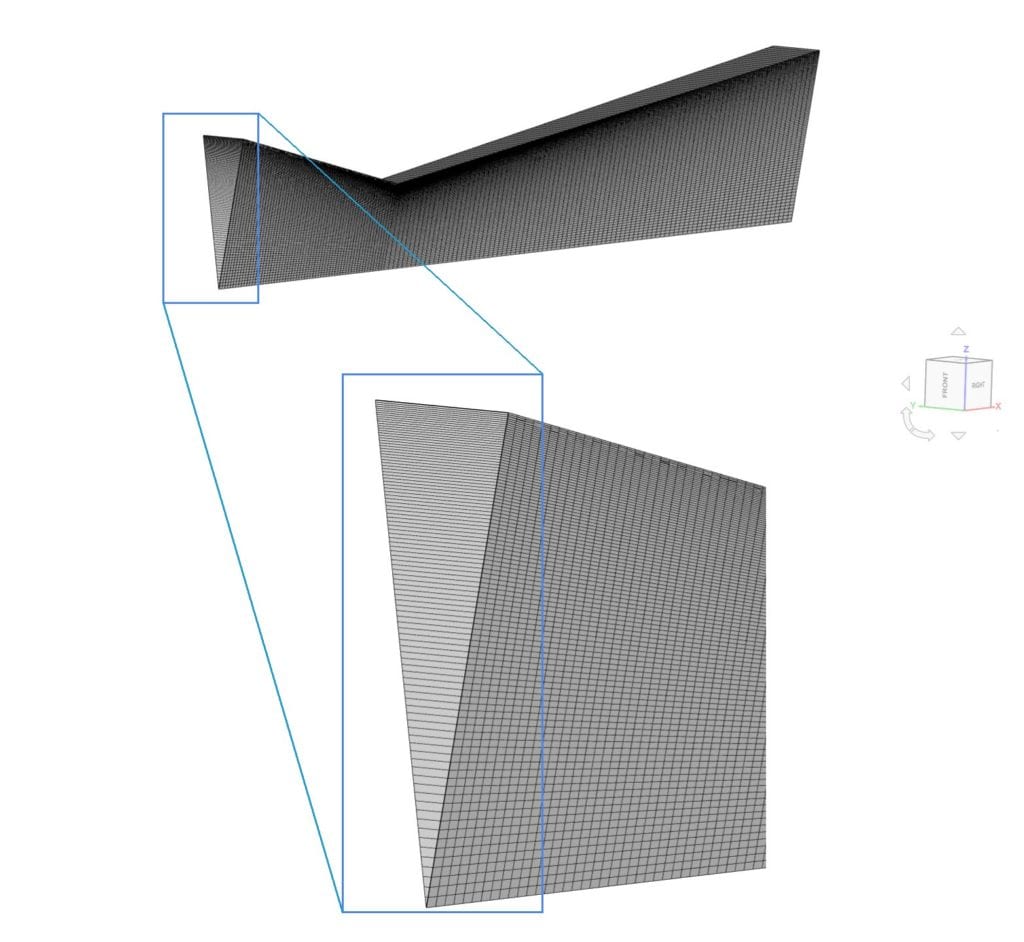
Mesh and Element types:

The hexahedral mesh was created externally and imported on to the SimScale platform, with an inflation of $y^{+}$ = 30 near the walls, as the ‘wall functions’ model was chosen. To keep the flow two-dimensional, the mesh was designed to have only one layer in the $y$ direction.

Mesh type	Cells in the x-direction	Cells in the y-direction	Cells in the z–direction	Number of nodes	Type
blockMesh	150	1	100	15000	2D Hex

Simulation Setup

Fluid:

• Custom He psi thermo type fluid:
  • Amount of substance: 1 mol
  • Molar mass: $M_m$ = 28.9 $\frac{kg}{kmol}$
  • Transport model: Sutherland
  • Reference viscosity: ${\nu }_0$ = 1.716e-5 $\frac{kg}{s\times m}$
  • Reference temperature: $T_0$ = 273.15 $K$
  • $T_s$ = 116 $K$
  • Thermo model: hconst
  • Specific heat: $C_p$ = 1005 $\frac{J}{kg\times K}$
  • Heat of formation: $H_f$ = 0 $\frac{J}{kg}$

Boundary Conditions:

Parameter	Inlet (ABC)	Outlet (GHI)	Wall (BEHIFC)	Wedges (AGHEB + AGIFC)
Velocity $[m/s]$	7.58	Zero Gradient	No-slip	Wedge
Pressure $[Pa]$	Zero Gradient	1.3×105	Zero Gradient	Wedge
Temperature $[K]$	300	Zero Gradient	Zero Gradient	Wedge
Turbulent kinetic energy $k$ $[m^2/s^2]$	0.862	Zero Gradient	Wall Function	Wedge
Specific dissipation rate $\omega$ $[s^{-1}]$	484.269	Zero Gradient	Wall Function	Wedge
Turbulent thermal diffusivity ${\alpha }_t$	Calculated	Calculated	Wall Function	Wedge
Turbulent dynamic viscosity ${\mu }_t$	Calculated	Calculated	Wall Function	Wedge

The wedge boundary condition is used in computational fluid dynamics to define an axisymmetric condition.

Reference Solution

The results are calculated from Bernoulli’s equation and the ideal gas equation. The speed of sound can be calculated as:

$$\begin{array}{}\text{(1)}& c=\sqrt{\frac{\gamma RT}{m}}\end{array}$$

Where:

• $\gamma$ is the specific heat ratio
• $T$ is the temperature
• $m$ is the molecular weight of the fluid
• $R$ is the universal gas constant

The Mach number of a cutting plane be calculated as:
$$\begin{array}{}\text{(2)}& M=\frac{U}{c}\end{array}$$

Where:

• $U$ is the average velocity magnitude of the plane

Finally, the static pressure can be computed as:

$$\begin{array}{}\text{(3)}& P_{stat}=P_{stag}–\frac{1}{2}\rho \times U^2\end{array}$$

Where:

• $P_{stag}$: the stagnation pressure, assumed to be 0.1301 $MPa$
• $\rho$: the density of the fluid

Result Comparison

A comparison of the Mach number and pressure variation in the nozzle obtained with SimScale over the AG line with analytical results is given below:

A source of deviation between the calculated and analytical results exists because the latter is calculated with a one-dimensional hypothesis. This means that all parameters are assumed to be uniform in the radial direction, while in the following figures, it seems that there exists radial variation too in the flow variables.

One can observe the radial variation causing results to slightly deviate:

Last updated: June 30th, 2025