The objective of this article is to explain how to predict Darcy and Forchheimer coefficients for perforated plates through an analytical approach, using empirical equations. Note that empirical equations are only suitable for single-phase flow.
Analytical Approach
Darcy–Forchheimer equation is an empirical equation, which relates the pressure loss, due to friction across a porous medium, with respect to the velocity of the flow inside the medium.
Friction is occurred by a combination of shear forces and pressure forces. While the shear forces are represented by a linear equation (Darcy equation), pressure forces are represented by a quadratic equation (Forchheimer equation). Therefore
Porosity
Porosity is the measure of empty space or the void percentage in a porous material. For a perforated plate of unit thickness porosity can be mathematically described as:
For circular holes, hydraulic diameter is the diameter of the hole. For non-circular conduit, the following equation can be used to calculate hydraulic diameter:
or
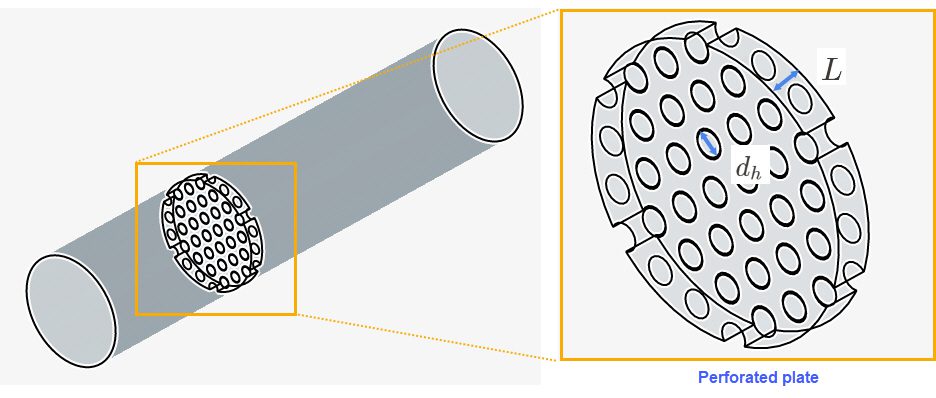
Where
Unconsolidated porous medium
An unconsolidated medium is a pile of solid particles packed inside a bed. Fluid flows around these particles.

If the medium is composed of uniform spherical particles, mean particle diameter (spherical particles) can be found as follows:
Darcy and Forchheimer coefficients can be calculated as follows:
Various studies were conducted to correlate pressure drop versus flow rate and geometry. With literature research, a convenient empirical equation should be found for specific perforated plate geometry and flow conditions. Here, we will show only two methods:
1st Model
The First equation is a simple approach proposed by Idelchik
Resistance coefficient:
Where,
Idelchik’s equation can be modified to be used as Forchheimer coefficient as follows:
Since Idelchik’s pressure coefficient is a quadratic resistance coefficient, one can assume the Darcy coefficient as zero:
2nd Model
The second equation is slightly more complex, modeled to differentiate thin and thick perforated plates
Discharge coefficient
Thin plates are assumed to have relatively large holes. For thin plates (L/dh)→0, resistance coefficient:
Thick plates are assumed to have relatively small holes. For thin plates (L/dh) » 0, resistance coefficient:
Resistance coefficient can be modified to be used as Forchheimer coefficient as follows:
Pressure loss with this method is also a quadratic function, therefore Darcy coefficient should be defined as zero:
You can use this spreadsheet to calculate
References
- Idelchik, I. E., Handbook of hydraulic resistance, third edition, CRC Press Inc., Boca Raton, US (1960)
- Kast W., (Revised by Hermann Nirschl), Gaddis E.S., Wirth KE., Stichlmair J. (2010) L1 Pressure Drop in Single-Phase Flow. In: VDI e. V. (eds) VDI Heat Atlas. VDI-Buch. Springer, Berlin, Heidelberg
- R. Bird, E. Lightfoot and W. Stewart, Transport phenomena, 2nd ed. New York: Wiley, 2007, pp. 190,191.
Important Information
If none of the above suggestions did solve your problem, then please post the issue on our forum or contact us.