Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Hyperelastic Equibiaxial Tension Test

    Validation Case: Hyperelastic Equibiaxial Tension Test

    This validation case belongs to an hyperelastic equibiaxial tension test in solid mechanics. The aim of this test case is to validate the following parameters:

    • Hyperelasticity under equibiaxial tension

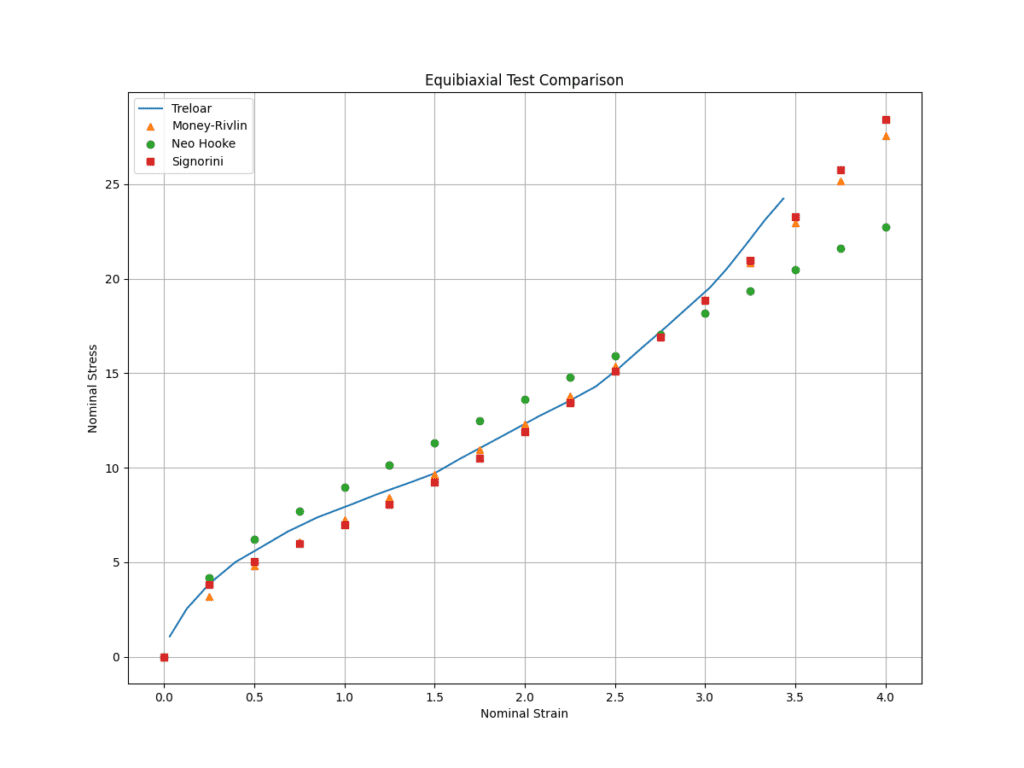
    The simulation results of SimScale were compared to the results derived from [Treloar]\(^1\).

    View Project

    Geometry

    The geometry used for the case is as follows:

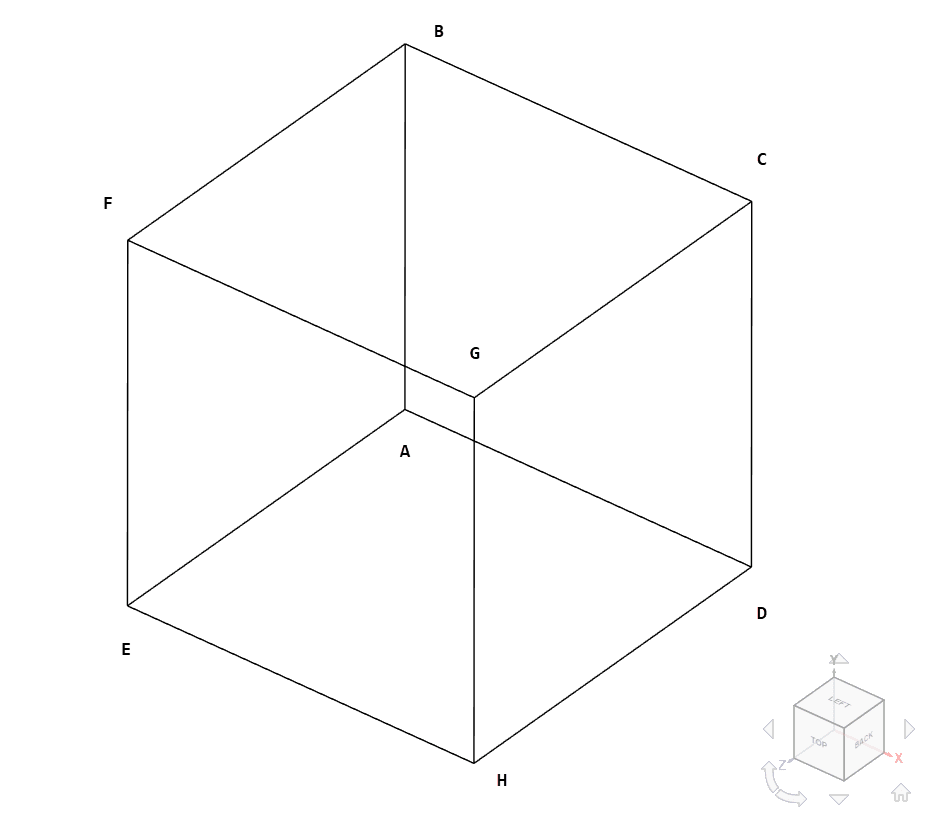
    cube geometrical model
    Figure 1: Geometry model for the cube

    The cube has an edge length of 1 \(m\).

    Analysis Type and Mesh

    Tool Type: Code_Aster

    Analysis Type: Static Non-Linear

    Mesh and Element Types:

    The mesh for the cube geometry was computed using SimScale’s Standard meshing algorithm.

    CaseMesh TypeNumber of
    Nodes    		Element Type
    AllStandard11841st order tetrahedral
    Table 1: Finite element model for each case
    tetrahedral mesh for uniaxial validation case simscale
    Figure 2: Tetrahedral element mesh for the cube

    Simulation Setup

    Material:

    Hyperelasticity material, with the following parameters for each type of law:

    • Neo Hooke:
      • \(C_{10} = \) 2.398 \(Pa\)
      • \(D_{1} = \) 1e-6 \(1/Pa\)
    • Mooney-Rivlin:
      • \(C_{10} = \) 1.751 \(Pa\)
      • \(C_{01} = \) 4.625e-2 \(Pa\)
      • \(D_{1} = \) 1e-6 \(1/Pa\)
    • Signorini:
      • \(C_{10} = \) 5.365 \(Pa\)
      • \(C_{01} = \) -2.477 \(Pa\)
      • \(C_{20} = \) 6.337e-1 \(Pa\)
      • \(D_{1} = \) 1e-6 \(1/Pa\)

    Boundary Conditions:

    • Constraints:
      • Face ABFE with zero x-displacement
      • Face AEHD with zero y-displacement
      • Face ABCD with zero z-displacement
      • Face DCGH with imposed 4 \(m\) x-displacement
      • Face BFGC with imposed 4 \(m\) y-displacement

    Reference Solution

    The reference solution is of the experimental type and was extracted from [Treloar]\(^1\). It corresponds with the nominal stress-strain material curve. The values were extracted using WebPlotDigitizer.

    Result Comparison

    Comparison of the nominal stress-strain curves computed from reaction force on the faces with zero displacement, versus the reference data is shown in Figure 3:

    nominal stress strain result curves comparison for equibiaxial validation case
    Figure 3: Nominal stress-strain curves comparison with Treloar \(^1\)

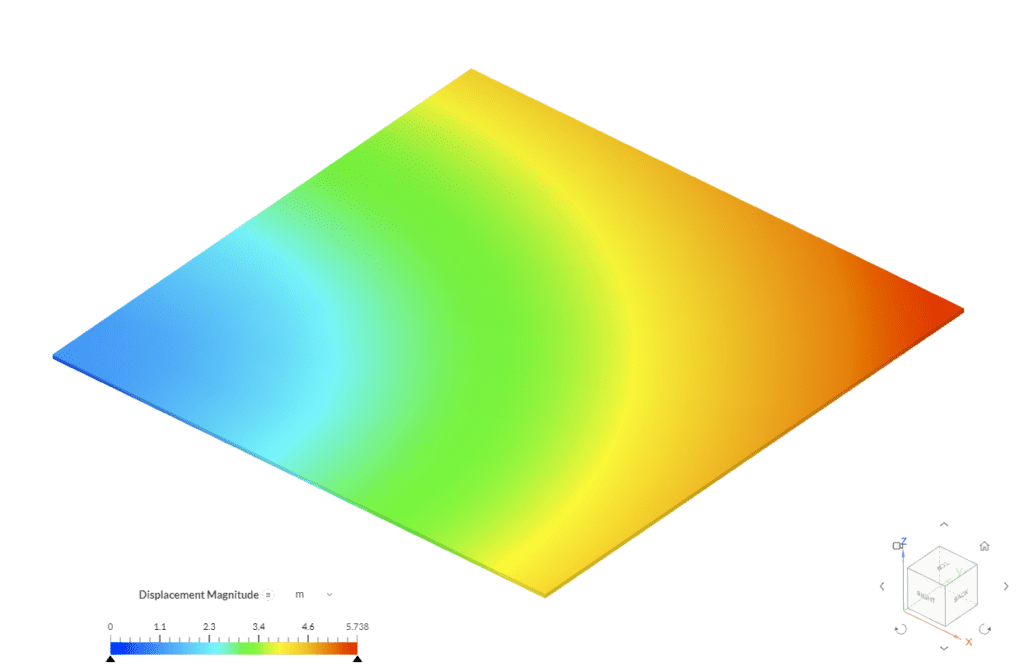
    Following are the contours of the final deformed shape and the von Mises stress from the Signorini case results, where the hyperelastic equibiaxial tension load effect can be appreciated:

    deformed shape color plot for equibiaxial validation case
    Figure 4: Final deformed shape of the cube, with color representing deformation magnitude for the Signorini case

    References

    • L. R. G. Treloar, “Stress-strain data for vulcanised rubber under various types of deformation”, Trans. Faraday Soc., 40:59–70, 1944.

    Note

    If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.

    Last updated: July 28th, 2021

    Contents