Validation Case: Hertzian Contact Between Two Spheres

This validation case belongs to structural dynamics. The aim of this test case is to validate the following parameters at the point of the Hertzian contact between two spheres:

• \(σ_{zz}\) stress using a frictionless penalty contact.
• \(σ_{zz}\) stress using a frictionless augmented Lagrange contact.

The simulation results of SimScale were compared to the results presented in [1].

Geometry

Only one-eighth of each of the two spheres (with a radius of 50 \(mm\) ) is used for the analysis due to the symmetry of the case study.

Analysis Type and Domain

Tool type: Code_Aster

Analysis type: Static nonlinear

Type of contact: Physical

Mesh and element types: The meshes were created with the standard meshing algorithm on the SimScale platform. While a single region refinement is used in the meshes (A) and (C), the meshes in (B) and (D) were created with an additional region refinement around the contact region.

Case	Element Type	Number of Nodes	Element Technology
(A)	1st Order Tetrahedral	1559	Standard
(B)	1st Order Tetrahedral	8229	Standard
(C)	2nd Order Tetrahedral	34320	Reduced Integration
(D)	2nd Order Tetrahedral	58973	Reduced Integration

Below the 1st order standard mesh for case A is visualized:

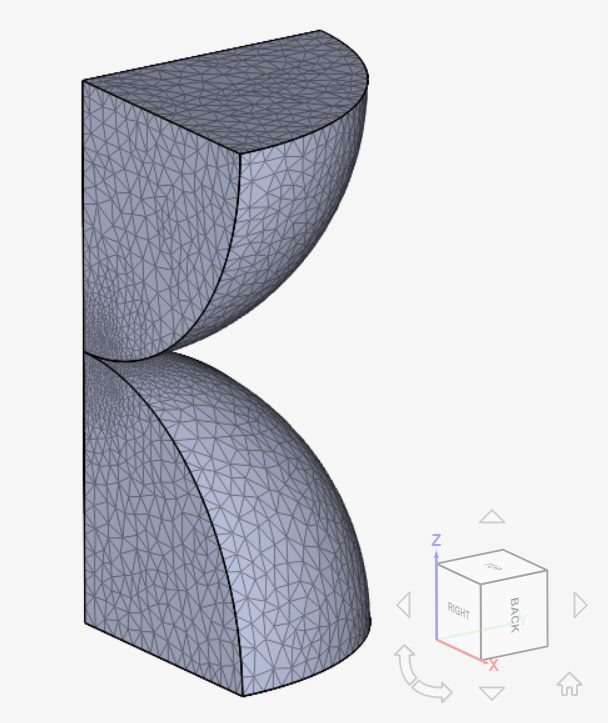
And the mesh (case B), which has a region refinement around the contact region is presented below:

Simulation Setup

Material/Solid:

• Isotropic:
  • \(E\) = 20 \(GPa\),
  • \(ν\)  = 0.3

Constraints:

• Faces ACD and A’C’D: zero x-displacement
• Faces ABD and A’B’D: zero y-displacement
• Face ABC: displacement of 2 \(mm\) in the z-direction
• Face A’B’C’ displacement of -2 \(mm\) in the z-direction

Physical Contacts:

• Augmented Lagrange:
  • Contact smoothing enabled for linear elements and disabled for quadratic elements
  • Frictionless
  • Augmentation coefficient = 100
• Penalty:
  • Contact smoothing enabled for linear elements and disabled for quadratic elements
  • Frictionless
  • Penalty coefficient = 10\(^{15}\)

Reference Solution

$$\sigma_{zz} = \frac{-E}{\pi}\frac{1}{1-{\nu}^2}\sqrt{\frac{2h}{R}} \tag{1}$$

$$h= 2 mm−(−2 mm ) = 4mm\tag{2} $$

With equation (1) and equation (2) the stress at point D results in:

$$\sigma_{zz} = −2798.3\ MPa$$

Results

Comparison of the stress \(σ_{zz}\) at point D of the Hertzian contact obtained with SimScale with the analytical result of the reference solution [SSNV104_A]\(^1\):

Case	Physical Contact	[SSNV104_A] (MPa)	SimScale (MPa)	Error (%)
(A)	Penalty	-2798.3	-2834.34	1.288%
(A)	Augmented Lagrange	-2798.3	-2836.32	1.359%
(B)	Penalty	-2798.3	-2834.97	1.310%
(B)	Augmented Lagrange	-2798.3	-2830.21	1.140%
(C)	Penalty	-2798.3	-2875.45	2.757%
(D)	Penalty	-2798.3	-2841.42	1.541%

It is obvious from the table above that the best results were obtained with SimScale’s 1st order mesh (case B), using the Augmented Lagrange contact:

Last updated: September 24th, 2021