websights

Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Free Vibrations on Elastic Support

    Validation Case: Free Vibrations on Elastic Support

    This validation case belongs to vibrations and the elastic support boundary condition in solid mechanics. The aim of this test case is to validate the following parameters:

    • Elastic support

    The simulation results of SimScale were compared to the results derived from [Schaum]\(^1\).

    View Project

    Geometry

    The geometry used for the case is as follows:

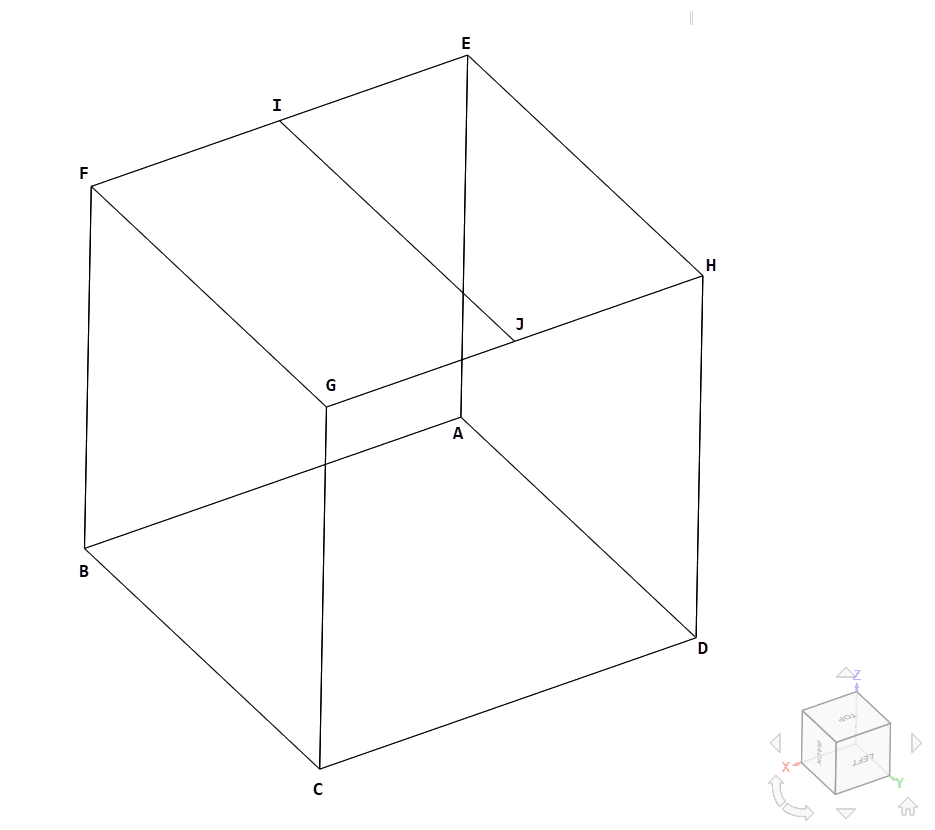
    geometry free vibration elastic support validation case
    Figure 1: Geometrical model of the cube.

    The cube has an edge length of 1 \(m\), with the upper face partitioned in half.

    Analysis Type and Mesh

    Tool Type: Code Aster

    Analysis Type: Static Linear and Dynamic

    Cases corresponding to analysis type are as follow:

    CaseAnalysis Type
    A-1Static Linear
    A-2Dynamic
    B-1Static Linear
    B-2Static Linear
    B-3Static Linear
    Table 1: Analysis type by case.

    Mesh and Element Types:

    Tetrahedral meshes were computed using SimScale’s standard mesh algorithm and manual sizing.

    CaseMesh TypeNumber of
    Nodes    		Number of
    Elements    		Element Type
    A-11st Order Tetrahedral 4597Standard
    A-21st Order Tetrahedral4597Standard
    B-11st Order Tetrahedral128405Standard
    B-21st Order Tetrahedral128405Standard
    B-31st Order Tetrahedral128405Standard
    Table 2: Finite elements model for each case.
    mesh free vibration elastic support validation case
    Figure 2: Tetrahedral mesh employed on case B.

    Simulation Setup

    Material:

    • Linear Elastic Isotropic:
      • \( E = \) 205 \(GPa \)
      • \( \nu = \) 0.28
      • \( \rho = \) 10 \(kg/m^3 \)

    Boundary Conditions:

    • Constraints:
      • Case A-1/A-2:
        • Total isotropic spring stiffness \( K = \) 9810 \(N/m\) on face EFGH
      • Case B-1:
        • Total isotropic spring stiffness \( K = \) 4905 \(N/m\) on face EIGJ
        • Total orthotropic spring stiffness \( K_x = K_y = K_z = \) 4905 \(N/m \) on face IFJH
      • Case B-2:
        • Distributed isotropic stiffness \( K/A = \) 9810 \(N/m^3\) on face EIGJ
        • Distributed orthotropic stiffness \( K_x/A = K_y/A = K_z/A = \) 9810 \(N/m^3 \) on face IFJH
      • Case B-3:
        • Total isotropic spring stiffness \( K = \) 1962 \( N/m \) on face EIGJ
        • Total orthotropic spring stiffness \( K_x = K_y = K_z = \) 1962 \( N/m^3 \) on face IFJH
        • Distributed isotropic spring stiffness \( K/A = \) 3924 \( N/m^3 \) on face EIGJ
        • Distributed orthotropic spring stiffness \( K_x/A = K_y/A = K_z/A = \) 3924 \( N/m^3 \)
        • Total isotropic spring stiffness of \( K = \) 1962 \( N/m \) on face EFGH
    • Loads:
      • Self weight with gravitational acceleration \( g = \) 9.81 \( m/s^2 \) in the \( -Z \) direction.

    The following table summarizes the elastic support boundary conditions by case:

    CaseElastic Support Type
    on Face EIGJ    		Elastic Support Type
    on Face IFJH    		Elastic Support Type
    on Face EFGH
    A-1––Isotropic Total
    A-2––Isotropic Total
    B-1Isotropic TotalOrthotropic Total–
    B-2Isotropic DistributedOrthotropic Distributed–
    B-3Isotropic
    Total+Distributed    		Orthotropic
    Total+Distributed    		Isotropic Total
    Table 3: Elastic support detail by case.

    Reference Solution

    The analytical solutions for the rotation angle \(\theta_B\) and maximum shear stress \(\tau_{max}\) are given by the following equations:

    Cases A-1, B-1, B-2, B-3:

    \( x = \frac{mg}{k} \tag{1} \)

    Case A-2:

    \( x(t) = V_0 \omega Sin(\omega t) + X_0 Cos(\omega t) \tag{2} \)

    \( \omega = \sqrt{ k / m} \tag{3} \)

    \( V_0 = -0.01 m/s \)

    \( X_0 = -0.02 m \)

    \( X_eq = -0.01 m \)

    \( 2 <= t <= 4 \)

    The computed reference solution is:

    \( x_{static} = 0.01\ m \)

    \( \omega = 31.32\ Rad/s \)

    \( x(t) = (-3.193*10^{-4})Sin(31.32t) – 0.01Cos(31.32t) \tag{4} \)

    *\( x(t) \) corresponding to the displacement with respect to the equilibrium position.

    Result Comparison

    Comparison of displacement DZ on static cases:

    CASEDZREFERROR
    A-10.010.010 %
    B-10.010.010 %
    B-20.010.010 %
    B-30.010.010 %
    Table 4: Error for computed solutions.

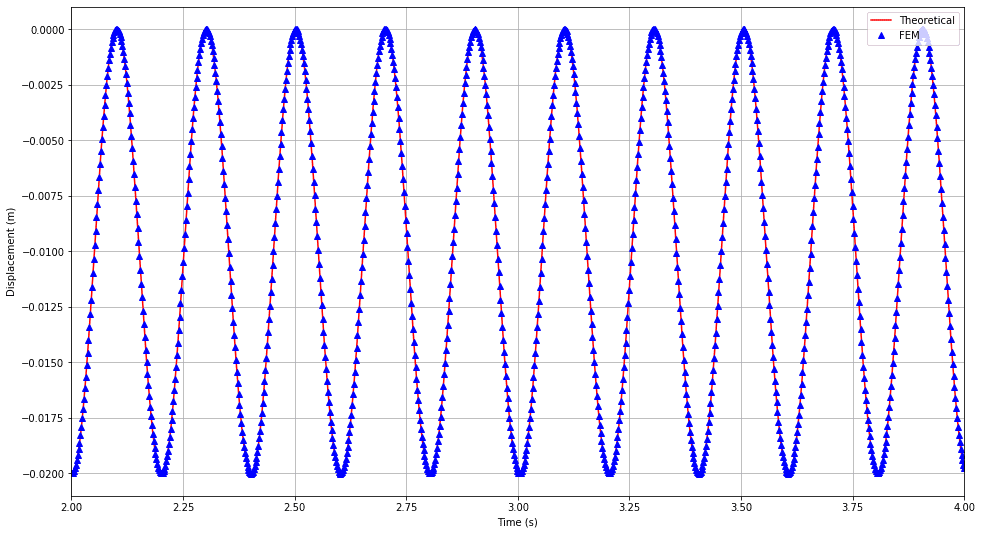
    Comparison of transient displacement of face ABCD in dynamic case can be found in Figure 3. Here the vibrations from the elastic support condition can be appreciated.

    displacement curve free vibration elastic support validation case
    Figure 3: Comparison of transient response oscillations.

    References

    • (2011)”McGraw-Hill Schaum’s outlines, Engineering Mechanics: Dynamics”, pg 271-273, N. W. Nelson, C. L. Best, W. J. McLean, Merle C. Potter

    Note

    If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.

    Last updated: October 8th, 2020

    Contents