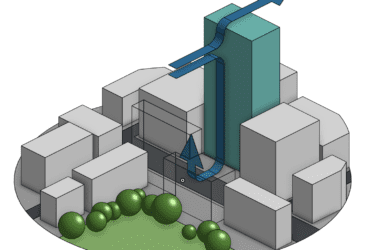
Computational fluid dynamics or CFD analysis is one of the key analysis methods used in engineering applications. The origins of and basics of CFD software lies in mankind’s efforts to better understand the power of natural elements like wind, storms, floods, or sea waves.
Flow Analysis What Do We Know About Flows?
The physical discipline of fluid dynamics evolved as the sciences started to classify the natural power and associated reaction of air, water or gases. This provided a systematic structure that embraced empirical laws and was derived from the idea of flow measurement that is used to solve practical problems. A typical fluid dynamics problem involves basic fluid properties like flow velocity, pressure, density, and temperature, in relation to time and space.
In everyday life, we can find fluid flows in meteorology (rain, wind, floods, hurricanes), heating, ventilation, and air conditioning, aerodynamic design, engine combustion, industrial processes, or the human body—for example, blood flow—and so on. Fluid dynamics has a wide range of applications, including calculating forces on aircraft, determining the mass flow rate of petroleum through pipelines, and predicting weather patterns.
CFD Analysis What is CFD?
Gas and liquid flow behavior is quantified by partial differential equations representing conservation laws for mass, momentum, and energy. Computational fluid dynamics is a branch of fluid mechanics that uses numerical analysis and algorithms to solve fluid flows situations. High-performing computers are used to conduct the calculations required to simulate the interaction of liquids and gases with surfaces defined by boundary conditions. [1]
Let’s start with some CFD basics. CFD software is based on the Navier-Stokes equations. Arising from applying Newton’s second law to fluid motion, together with the assumption that the stress in the fluid is the sum of a diffusing viscous term and a pressure term, these equations describe how the velocity, pressure, temperature, and density of a moving fluid are correlated. [2]
The development of CFD and the increase in CFD software applications has been closely associated with the evolution of high-speed computers.
Learn how a ducting system design was optimized with CFD 100% via web browser.
CFD Basics Brief History of CFD
1922 – Basis of modern CFD and numerical meteorology made by Lewis Fry Richardson in a weather forecasting scheme using differential equations and finite differences [3];
1933 – Earliest numerical solution for flow past a cylinder developed by A. Thom [4]1950 – First 24-hour weather forecast performed by the ENIAC modern computer [5]1955 – Particle-in-cell simulation method for transient 2D fluid flow developed by Los Alamos National Lab [6]1963 – Vorticity-stream-function method for 2D, transient, incompressible flow [7]1965 – Marker-and-cell method for time-dependent viscous flow developed by Los Alamos National Lab [8]1966 – Fluid-in-cell method developed for unsteady compressible flow problems [9]1967 – First 3D model based on panels discretization published by Douglas Aircraft [10]1968 – First lifting Panel Code (A230) described by Boeing Aircraft [11]1970 – First description of Full Potential equations published by Boeing [12]1981 – 3D FLO57 code based on Euler equations for transonic flows [13]After 1981 – Many of the fundamental pieces of research that contributed to CFD 2D and 3D methods focused on airfoil design and analysis. NASA research dedicated to the Navier–Stokes equations developed 2D codes ARC2D and 3D codes. These included codes like ARC3D, OVERFLOW, and CFL3D, which were the main sources for modern commercial CFD packages covering CFD basics.
CFD Applications Importance Why is It Important to Use CFD Analysis?
With a CFD analysis, we can understand the flow and heat transfer throughout the design process. The basic methodology for any engineering CFD software analysis is based on a few procedures:
• Understanding flow model — Flow separations, transient effect, physical interactions;
• Proving assumed model — Experimental results validation, parametric studies, structural simulations;
• Model optimizing — Reducing pressure drops, flow homogenization, improving laminar and turbulent mixing.
Without numerical simulations of fluid flow, it is very difficult to imagine how:
• Meteorologists can forecast the weather and warn of natural disasters;
• Vehicle designers can improve aerodynamic characteristics;
• Architects can design energy-saving and safe-living environments;
• Oil and gas engineers can design and maintain optimal pipes networks;
• Doctors can prevent and cure arterial diseases by computational hemodynamic.
CFD Analysis Performing Sophisticated CFD Simulations with SimScale
CFD analysis of a Formula One car carried out in a web browser with SimScale
In relation to mechanical fluid simulation, fluid dynamics is one of the key analyses methods used by the SimScale platform together with solid mechanics and thermodynamics. SimScale offers a wide variety of CFD software analysis capabilities, including:
• Multiple laminar and turbulence models, which are based on the Reynolds number for the fluid flow;
• Steady-state applications and transient solvers setup;
• Mass transport within fluid flows;
• Access to multiple incompressible and compressible fluids solvers;
• Single- and multiphase flows simulation;
• Advanced modeling concepts, such as porous media or rigid body movement of fluid domains
CFD Basics: Templates Templates in Public Projects Library
To better illustrate the multitude of applications for CFD analysis, let’s take a look at some CFD basics and relevant examples that are available in the SimScale Public Projects Library:
Many projects are related to the aerodynamic analysis of different vehicles, such as F1 cars or motorbike turbulence airflow simulation.
In the course of a football or basketball game, the ball can often take unpredictable trajectories. This project shows how a flow analysis can be used to investigate the aerodynamic behavior of a football.
During a free workshop on Formula 1 aerodynamics, Nic Perrin provided a lot of great insights into the fascinating aerodynamics of a race car, such as the interaction between the front wing and the wheels, or how the vortices help to improve the downforce.
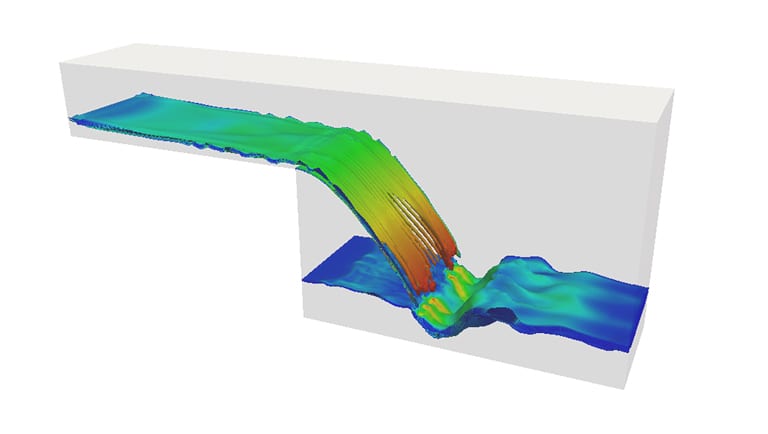
An interesting multiphase flow analysis is this free surface simulation of a waterfall. Here is a simple flow simulation of a globe valve where the results can be analyzed and visualized in the integrated post-processing environment.
The projects related to theoretical models research are extremely important as these assumptions are the foundation for real cases studies.
Here is an example of a non-Newtonian flow analysis through a sudden expansion. For a more detailed study, please go to “non-Newtonian flow through an expansion channel” documentation. This project validates the flow velocity profile for a non-Newtonian fluid via the steady state Reynolds-averaged Navier–Stokes (RANS) approach and Power-Law model for non-Newtonian fluids.
All of the projects presented in this article (and CFD basics learned) can be imported into your own workspace and used as templates. All you need to do is create a free Comunity account here and then copy any of these simulations. Feel free to browse the Public Projects Library for other interesting analyses.
To learn how to use them and set up your own simulation with SimScale, watch the recording of the CFD Master Class (session 1). Just fill out this short form and it will play automatically.
References
- Wikipedia, Computational fluid dynamics
- Wikipedia, Navier-Stokes Equations
- Richardson L.F. – “Weather Prediction by Numerical Process”, Cambridge University Press, 1922, Reprinted by Dover Publications, New York, 1965
- Thom A. – “The Flow Past Circular Cylinders at Low Speeds”, Royal Society, 651-666, London, 1933
- Lynch P. – “The origins of computer weather prediction and climate modeling”, Journal of Computational Physics, University of Miami, 2008
- Harlow F.H. – “A Machine Calculation Method for Hydrodynamic Problems”, Los Alamos Scientific Laboratory, 1956
- Fromm, J. E., Harlow, F. H. – “Numerical solution of the problem of vortex street development”, Physics of Fluids 6: 975, 1963
- Harlow, F. H. Welch J. E., “Numerical calculation of time-dependent viscous incompressible flow of fluid with a free surface”, Physics of Fluids 8: 2182–2189, 1965
- Gentry, R. A., Martin, R. E., Daly, J. B. – “A Eulerian differencing method for unsteady compressible flow problems”. Journal of Computational Physics 1: 87–118, 1966
- Hess, J.L. Smith A.M.O., – “Calculation of Potential Flow about Arbitrary Bodies”. Progress in Aerospace Sciences 8: 1–138, 1967
- Rubbert, P., Saaris, G. – “Review and Evaluation of a Three-Dimensional Lifting Potential Flow Analysis Method for Arbitrary Configurations,” AIAA paper, 72-188, 1968
- Murman, E., Cole, J. – “Calculation of Plane Steady Transonic Flow,” AIAA paper, 1970
- Jameson, A., Schmidt, W. and Turkel, E. – “Numerical Solution of the Euler Equations by Finite Volume Methods Using Runge-Kutta Time-Stepping Schemes,” AIAA paper 81-1259, 1981