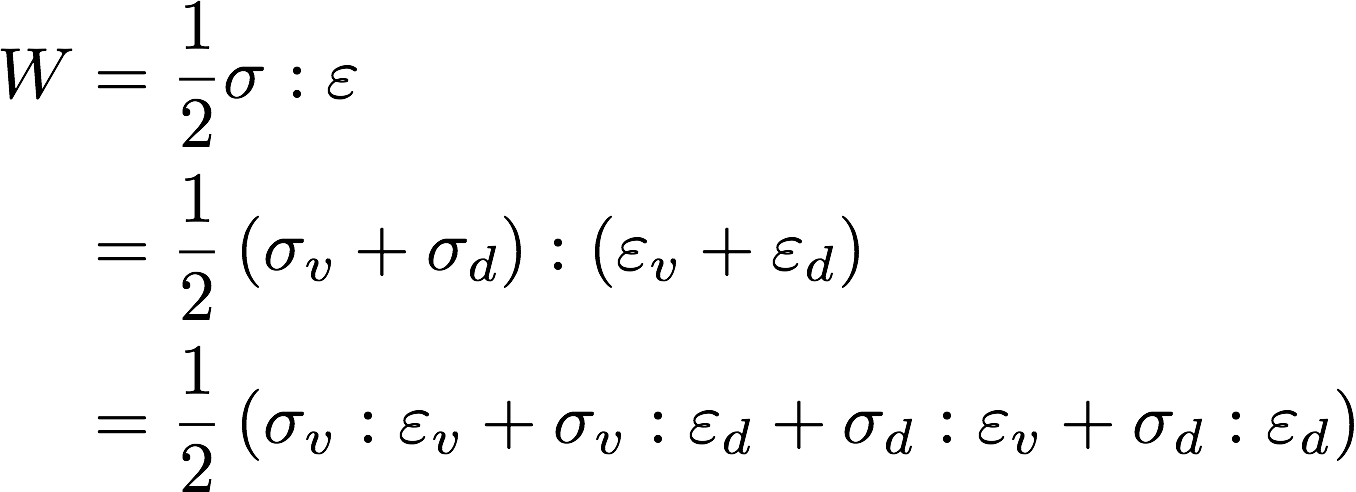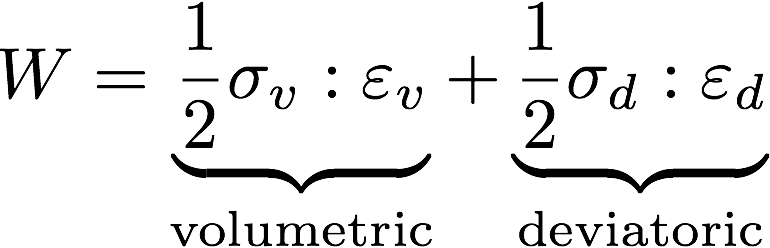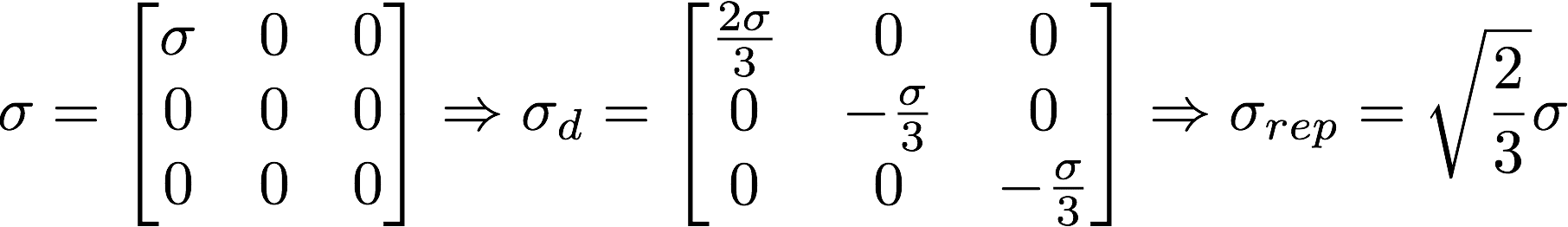The idea of von Mises stress was first proposed by Maksymilian Huber in 1904. However, it only received real attention in 1913 when Richard von Mises proposed it again. While both only proposed a math equation, it was Heinrich Hencky who developed the idea of “von Mises stress” as a reasonable physical interpretation.
Let’s start by considering a simple uniaxial tensile test on an isotropic and ductile specimen.
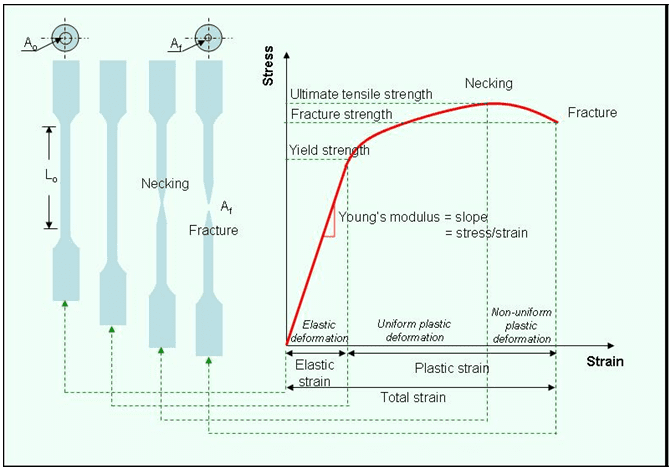
As shown in Fig. 01, the material starts to deform elastically up to the elastic (or yield) limit, followed by some “yielding”, “necking” and finally breaking at the ultimate stress.
This point (or stress) at which the material behavior transforms from elastic to plastic behavior is known as “yield stress”. We often say that the material yields if the stress is greater than the yield strength. However, it is important to note that the stress is a tensor and not a single number (or scalar). Let’s say the material was being pulled along the x-x direction. It is technically accurate to say that the material starts to yield when the x-x component of stress is greater than the yield stress.
However, in real life applications, the stress tensors are more generic and not essentially uniaxial. It is likely that each component of the stress tensor is non-zero. In such a case, how can one say that the material has started to yield? Or how can we design components so that one is certain that we are within the yield limit? What is that scalar number that we can use to compare with the yield stress found experimentally?
The purpose of a helmet is to protect the person who wears it from a head injury during impact. In this project, the impact of a human skull with and without a helmet was simulated with a nonlinear dynamic analysis. Download this case study for free.
von Mises stress Important Terminology in Plasticity and Inelastic Modeling
To proceed further, it is necessary to understand some essential and frequently used terminology in the area of plasticity and inelastic modeling. The stress tensor has six independent components and can be decomposed into volumetric (or hydrostatic) and deviatoric parts. Similarly, the strain tensor can also be decomposed into the analog strains.
Mathematically, the volumetric strain and stress can be defined as one-third of the trace of the strain and stress tensor. The difference yields the deviatoric stress.
The volumetric strain purely corresponds to a change in volume of the object without any changes in the overall shape. This is like scaling an object. In contrast, deviatoric strain corresponds to the shearing and distortion effects observed.
Distortion Energy and von Mises Stress
Now that we understand the idea of volumetric and deviatoric strains, we can go ahead and define the distortion energy.
We should always remember that the mechanical behavior of materials is also governed by the two laws of thermodynamics. As per the first law of thermodynamics, energy is neither created nor destroyed. It is only converted from one form to another. So, when a mechanical force acts on a body (or upon application of a prescribed displacement), some work is being placed on the body. This energy is stored in as strain energy in the body. Strain energy density is defined as:
In other words, this is the total strain energy stored in each differential volume of the body. If this strain energy is summed over all the differential volumes (or otherwise called integration over the entire volume), we can obtain the total strain energy stored in the body.
Out of this total energy, a part goes into changing the volume of the material (or volumetric strain) and is otherwise known as volumetric energy. The rest of the energy is used to distort the shape of the material and is otherwise known as deviatoric energy. The von Mises stress is related to this total stress component going into the distortion energy. Or in mathematical terms:
where subscripts v and d represent the volumetric and deviatoric parts respectively. However, the product of any volumetric and deviatoric tensor is always zero. Thus, the strain energy density reduces to:
where the total energy can be written in terms of volumetric and deviatoric parts. Now, we can rewrite the deviatoric strain energy through a “scalar representative stress” as:
The representative stress here is the von Mises stress. Taking a leaf out of the 1-D stress state, the von Mises stress can be rewritten as:
Principal Stress
The next important issue to consider is the idea of principal stresses. In a generic situation, the stress is a full symmetric matrix. In this situation, it is difficult to make design decisions considering data from simple uniaxial experiments. However, in any situation, there will exist a plane that is subjected to pure volumetric loading. Rotating a general stress tensor leads to a diagonal matrix. The diagonal elements are known as principal stresses.
Wouldn’t it be interesting to see the von Mises stress in a real simulation and not only in theory? You can attend our free on-demand FEA Master Class and get a practical grasp of this interesting topic!
von Mises stress Von Mises Yield Criterion
The term derived above, with the square root of 2/3, for the representative or “von Mises” stress, looks familiar! The three principal stresses can be treated as coordinates and the resulting von Mises stress can be plotted.
Fig. 02 illustrates the yield criterion in the principal stress space. Any stress state can be converted to the three principal stresses, which, if considered the three coordinates, the von Mises stress for different combinations leads to a cylindrical surface as shown in Fig. 02.
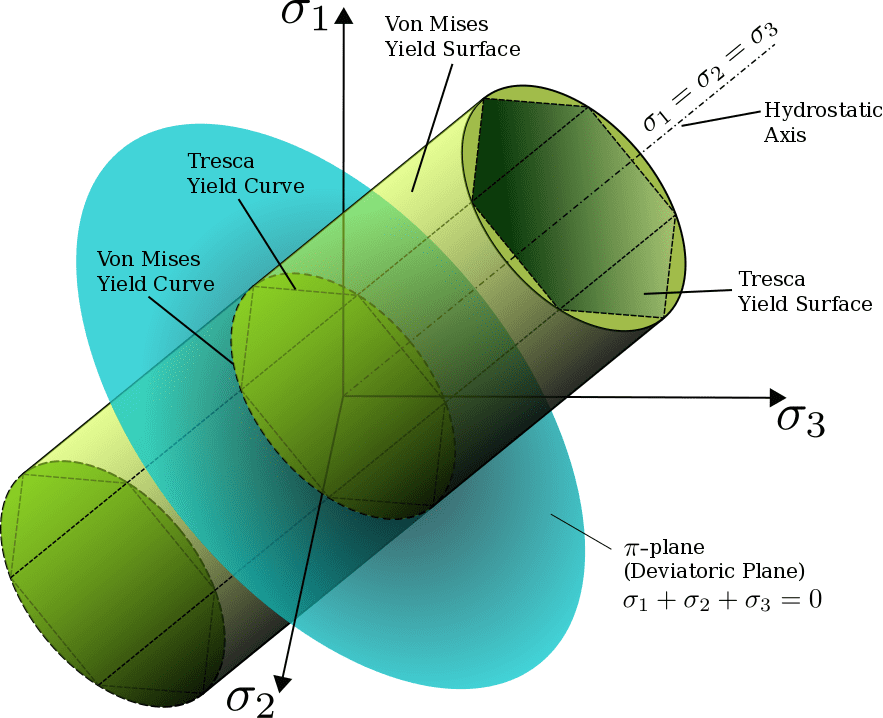
In other words, this means that if the stress state at any point is on the cylinder, then the material has started to yield at this point in the structure. Similarly, the Tresca yield criterion is defined based on the maximum possible normal and shear stresses that the material can withstand.
von Mises stress Conclusion
Most often, structures consist of materials like steel that show a plastic deformation and yielding before undergoing fracture. It is always preferred to design structures so that they are within the elastic limit and do not yield. While most of the experiments are simple loading conditions (like uniaxial tensile), designers are often in a quandary as to how this can be related to generic loading conditions observed in reality.
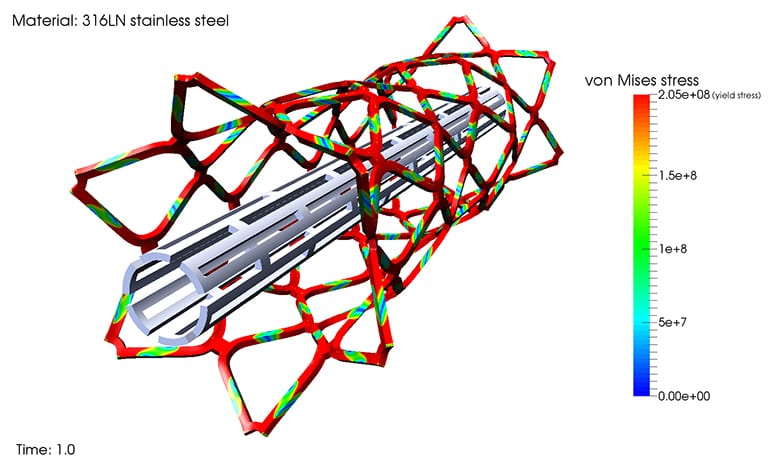
The von Mises stress, though it sounds fancy, is just a metric of measurement to determine whether the structure has started to yield at any point. The stresses calculated at any point can be mathematically written into a scalar quantity known as von Mises stress, which can then be compared with experimentally observed yield points.
If you’d like to learn more about finite element analysis with a simulation software, here is a static stress analysis of a Toyota Hilux bumper ran 100% in a web browser. Just create a free Community account here and copy this simulation to use it as a template.
To see cloud-based simulation in action, watch the recording of the “Bike Frame Structural Analysis with FEM” webinar by filling out this short form.