We often hear the terms “modal analysis,” “eigenvalues,” “eigenmodes” or “eigenfrequencies”, and by the time one comprehends a single terminology, a new terminology emerges. People always prefer to make things sound more complicated than they need to be. More often these terms develop out of necessity, but many times it’s to express things with mathematical accuracy. Let’s briefly explain the difference between quasi-static, dynamic, and modal analysis.
Modal Analysis What Is Modal Analysis?
The most common type of analysis is quasi-static analysis, where the load is applied at a very slow rate so that the acceleration is negligible (or almost zero). Dynamic analysis is where the effects of acceleration cannot be ignored. Both types provide a one-to-one relationship between a particular input (for example, a force applied on a system) to its system response (for example, a displacement of the system due to its load).
In contrast to quasi-static and dynamic, modal analysis provides an overview of the limits of the response of a system. For example, for a particular input (like an applied load of certain amplitude and frequency), what are the limits of the system’s response (for example, when and what is the maximum displacement).
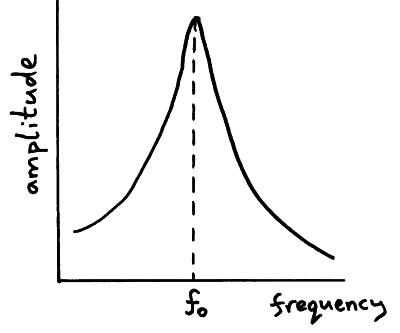
As shown in Fig. 01, every object has an internal frequency (or resonant frequency) at which the object can naturally vibrate. It is also the frequency where the object will allow a transfer of energy from one form to another with minimal loss—here it is from vibrational to kinetic. As the frequency increases towards the “resonant frequency,” the amplitude of response asymptotically increases to infinity. In other words, the results of modal analysis are these frequencies at which the amplitude increases to infinity.
Modal Metrics How Are Eigenvalues, Eigenvectors, and Eigenmodes Related?
Any object can be considered a connection of complicated springs, and then the system response “x” for any applied input “y” could be given using a scaling factor as
$$ k \cdot x = y $$
This is similar to the spring equation where “k” is the spring stiffness, “x” is the spring displacement and “y” is the applied force. For any generic system, it can be written as
$$ [K] \{x\} = \{y\} $$
where \(\{x\}\) can be displacements, temperatures, etc., while \(\{y\}\) is a force, flux, etc. The matrix \([K]\) can be considered a scaling factor, and it is more commonly known as a stiffness matrix. Now, for some response \(\{x\}=\{a\}\), if the applied input was \(\{y\}=L\cdot \{a\}\), then \(L\) are known as the eigenvalues, and the response of the system \(\{a\}\) are known as the eigenvectors corresponding to the eigenvalue \(L\).
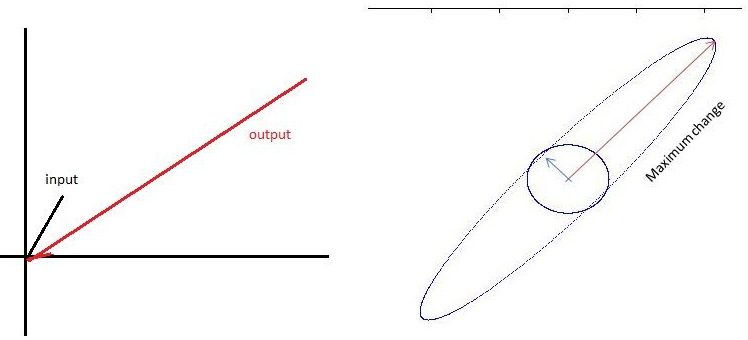
In other words, as shown in Figure 2, the magnitude of the applied input and its response are just a multiple. The eigenfrequencies are those at which this scaling is maximum (i.e., the eigenvalue).
Modal Analysis So Why Are These Frequencies Important?
Every system can be described in terms of a stiffness matrix that connects the displacements (or system response) and forces (or system inputs). These frequencies are known as natural frequencies of the system and are provided by the eigenvectors of the stiffness matrix. These frequencies are also known as the resonant frequencies.
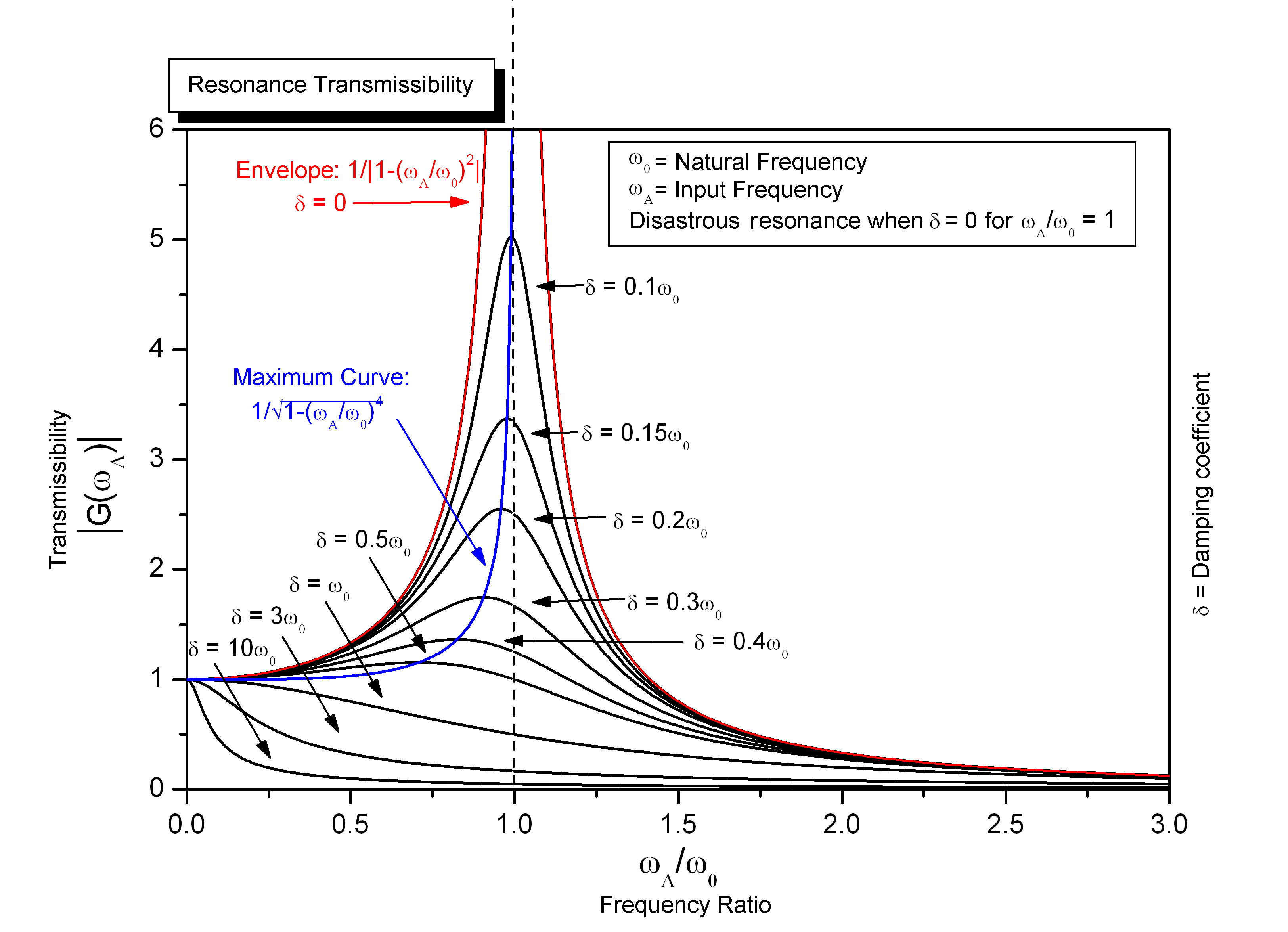
The resonant frequencies related to mechanical structures are known as mechanical resonance. Similarly, every system—like acoustic, thermal, or electromagnetic—has its own resonant frequencies at which resonance occurs. As illustrated in Figure 3, as the frequency of the applied load (or input on the x-axis) nears the resonant frequency, the amplitude of response (on the y-axis) nears infinity!
As governed by the first law of thermodynamics, one form of energy is only converted to another. However, energy is neither created nor destroyed. In any mechanical system, when an external time-varying load is applied, it is equivalent to supplying the system with some kinetic or vibrational energy. This is transmitted through the system resulting in a displacement of the structure. However, due to the presence of friction, some of this energy is also dissipated as heat.
To understand this process more physically, imagine that structure is in a constant state of motion sub-atomically. The energy supplied is transported from one part of the structure to the other through energy transfer by atomic processes. However, when the frequency of loading is the same as the averaged vibrational frequency of the atoms in the structure, the energy is transferred with minimum loss. In other words, one can think of it as two waves (one being the external load and the other being that of the internal atomic structure) that are being superimposed. When the frequencies are the same, they tend to add up.
Therefore, it is important to know the frequencies at which the structure can behave erratically.
Modal Examples Practical Examples for Modal Analysis
There are several examples where a prior accurate modal analysis could have prevented loss of lives and property. Some famous ones include:
Tacoma Narrows Bridge Disaster of 1940
The Tacoma Narrows Bridge was built in the state of Washington (USA). On November 7, 1940, at around 11 a.m., the bridge came down instantaneously. A later investigation revealed that the cause of the collapse was aeroelastic flutter.

In simpler terms, it was a wind-induced collapse. The winds were blowing at a particular frequency, which happened to coincide with the resonant frequency of the structure, resulting in the sudden collapse of the structure.
Mexico City Earthquake of 1985
Another real-life example was the 1985 earthquake in Mexico City. The energy released during this earthquake was equivalent to 1114 nuclear detonations, and the earthquake was felt as far as Los Angeles, which is over 2500 km away. Up to the 1950s, no earthquake codes existed. It wasn’t until the later 1950s and 1970s that earthquake codes were developed and introduced for building construction. Despite this, none of these safety precautions accounted for an event of magnitude 7.0 plus, which is exactly what occurred in Mexico City in 1985.
During the earthquake, most of the 6 to 15-story high-rises collapsed, resulting in huge loss of life and property. Interestingly, buildings with less than 6 or more than 15 stories were not damaged as much, while buildings with 9 stories were completely destroyed to rubble! Two explanations were offered for the earthquakes’ impact: the duration of the shaking and the resulting resonance with the lakebed frequency. In other words, the resonant frequency of the 6 to 15-story structures coincided almost exactly with the frequency of the earthquake.
At present, there are several earthquake codes being implemented by civil engineers that are specifically for structures being built in a zone that is vulnerable to earthquakes.
Taipei 101 and Burj Khalifa
A real-life example can be seen in today’s skyscrapers like Taipei 101 in Taipei City, Taiwan, or Burj Khalifa in Dubai (UAE). These megastructures use tuned mass dampers to absorb the energy and dampen the oscillations of the structures.
Taipei 101 experiences complex local wind systems that swirl around the structures. The building acts like a large sail of a boat, causing vortex shedding, twisting, or bending the structures in unimaginable ways. Taipei 101 uses a tuned mass damper in the form of a large pendulum between the 88th and 92nd floors. A video of the workings of the pendulum is available on YouTube, as shown below:
The Burj Khalifa is known to oscillate about 5-6 ft at the top. These large motions can be felt as creaking and can be significantly uncomfortable for the inhabitants. For this reason, the Burj Khalifa does not use a damper system. Instead, they change the external profile of the building based on the wind system, thus reducing the overall force of the wind.
Explore FEA in SimScale
Modal Analysis Conclusion
To summarize, we have examined the meaning of modal analysis and various nomenclature. It is critical that a designer understands the natural vibration frequencies of a system in order to ensure that they are not the same as excitation frequencies, thus ensuring safety standards. This is a key component in many fields like civil, aerospace, or automotive engineering where loss of life and property is a major concern.
Starting with hand calculations in the 1980s, computer simulations have made great breakthroughs to help improve the quality and robustness of design processes. We look forward to the day when computer simulations can replace engineering codes!
If you’d like to see how cloud-based engineering simulation can be used in civil engineering, watch the recording of the “How to Predict Wind Loads with CFD” webinar. Just fill out this short form and it will play automatically.
In addition, this article might be interesting for you to read → Why the Tacoma Narrows Bridge Collapsed: An Engineering Analysis.