Choosing realistic boundary conditions is one of the most important and challenging parts of setting up a simulation. It is not necessarily difficult to find a combination that works, but it is essential to produce meaningful results instead of random numbers.
This raises the question: what is the right boundary condition, and what kind of magic should I master to find it? In the following, the basics required to make informed decisions regarding boundary conditions will be reviewed. In addition, you will better understand each of them, starting with Dirichlet, Neumann, and Robin.
Boundary Conditions Dirichlet, Neumann or Robin?
Quite expectedly, there is often not one right answer, but several boundary conditions that make sense. It depends on the purpose of the particular simulation. Thus the first port of call is understanding what the expected real-world behavior is. Secondly, understanding how such behavior is modeled in the software is imperative.
The challenge lies in the fact that there is never a one-to-one mapping between these two worlds. Therefore, it would be helpful to learn a bit more about the theory behind each type of boundary condition. Then a meaningful correlation between the simulated phenomena and software capabilities can be established.
Boundary conditions bring the influence of the outside world into the simulation domain. On a theoretical level, they are constraints applied to the governing equations of the system and are categorized accordingly:
- Dirichlet boundary condition specifies the value of a variable at a boundary. It may also be called a fixed condition. Therefore, it is used when a value needs to be imposed at a boundary. For example, a no-slip condition in fluid mechanics is a Dirichlet condition because it sets the value of the velocity to zero. In solid mechanics, prescribing a certain load or displacement, and in heat transfer—setting the temperature at a surface are other examples of this type of condition.
- Neumann boundary condition specifies the derivative of a variable at a boundary. It is used rather than the actual value when a certain rate of change in value needs to be imposed for a variable. A common example in fluid mechanics is the fully developed condition at an outlet where the gradient of flow variables is set to zero. Traction conditions in solid mechanics and insulated surfaces in heat transfer are other examples.
- Robin boundary condition specifies a combination of the value and the derivative of a variable at a boundary. Therefore, these conditions are suited for more complex behavior. For example, in heat transfer, Robin conditions are used to model Newton’s law of cooling, where heat flux (derivative) is proportional to temperature (value). However, Robin conditions are not the only class of boundary conditions that utilize value and derivative to specify a condition, but this is another discussion.
- There are other boundary conditions besides Dirichlet, Neumann, and Robin that exploit certain flow features. For example, in scenarios where the domain features spatial symmetry, the size of the domain, and therefore the computational effort, is reduced by using symmetry boundaries. Similarly, periodic conditions are used to simulate periodicity effects without having to run computations on the full domain. Thus boundary conditions can be used to effectively gain an advantage.
SimScale’s CEO David Heiny tests the capabilities of cloud-based simulation to solve an engineering problem. Fill out the form and watch this free webinar recording to learn more!
Boundary Conditions Testing Your Boundary Conditions Choice
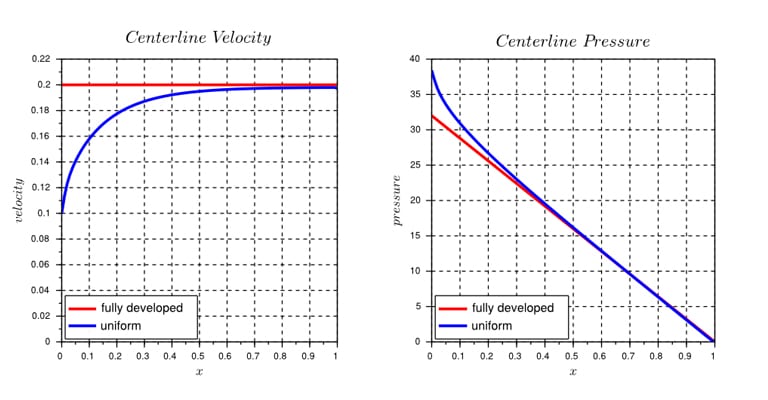
It is now easier to approach the problem methodically. Once the type of condition that is required is pinned down, it is time to test the hypothesis in detail. Here is an example: Assume a simple case of incompressible pipe flow. Given a flow rate, the pressure drop between the inlet and outlet needs to be calculated.
Would this problem have a unique answer? No. As can be seen in the following figure, the choice of the velocity profile will affect pressure drop. In this case, the uniform velocity profile at inlet results in an 18% larger pressure drop.
Even though the boundary condition type is chosen correctly, the decision of inlet profile will change the result of the simulation noticeably. Therefore, ensure to examine all aspects of the setup thoroughly.
In the end, it is not always feasible to make a decision without actually running any simulations. Therefore, it is helpful to run the simulation with different combinations in a controlled setup and study the validity of each result.
Such a setup should be simple enough so that the influence of the boundary condition choice can be meaningfully interpreted. Once a certain choice has proven successful, it can be used in the full simulation.
Finally, in addition to knowledge, an experienced analyst relies on the experience gleaned from running multiple simulations. Therefore, do not be afraid to experiment with simulations, because practice makes perfect!