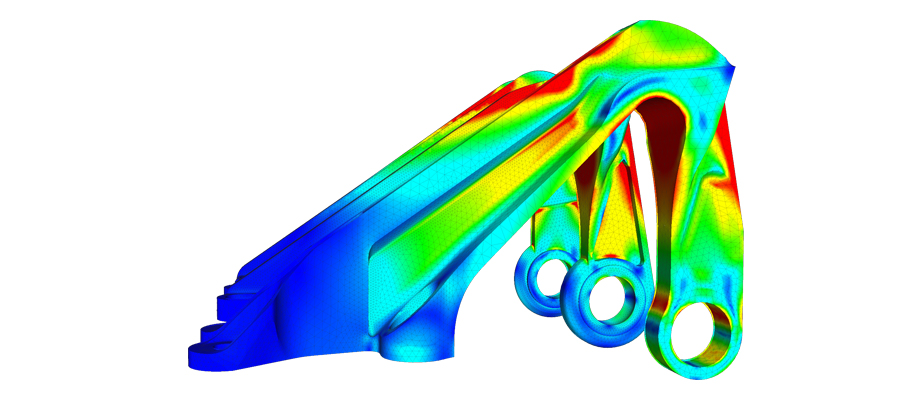
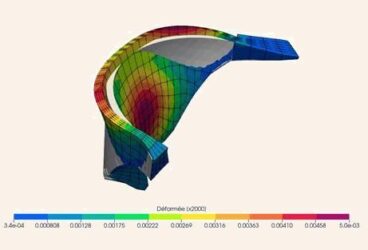
What is the Finite Element Method (FEM)?
The finite element method (FEM) is a numerical problem-solving methodology commonly used across multiple engineering disciplines for numerous applications such as structural analysis, fluid flow, heat transfer, mass transport, and anything existing as a real-world force. This practice systematically yields equations and attempts to approximate the values of the unknowns. This method subdivides the overall problem into simpler sub-issues that are easier to solve. In turn, these sub-issues called finite elements require implicit vs explicit analysis.
Why is the Finite Element Method Necessary?
Implicit vs Explicit FEM is used to simulate naturally or artificially occurring phenomenons. This numerical technique is the foundation of simulation software in order for engineers including civil and mechanical engineers to assess their designs for tension, weak spots, etc., before prototyping or implementation stages.

Implicit vs. Explicit FEA Time-dependent vs. Time-independent Analysis
For all nonlinear and non-static analyses, incremental load (also known as displacement steps) are needed. In more simplistic terminology, this means we need to break down the physics/time relationship to solve a mathematical problem. To do this, we form two groups: either time-dependent or time-independent problems. To solve these problems, we commonly use ‘implicit’ and/or ‘explicit’ methods.
We refer to problems as ‘time-dependent’ when the effects of acceleration are pronounced and cannot be neglected. For example, in a drop test, the highest force occurs within the first few milliseconds as the item decelerates to a halt. In this case, the effect of such a deceleration must be accounted for.
In contrast, when loads are slowly applied onto a structure or surface (i.e., when a monitor is placed onto a table) the loading can be considered ‘quasi-static’ or ‘time-independent’. This is because the loading time is slow enough that the acceleration effects are negligible. For more time-dependent and time-independent examples, there are several projects in the SimScale Public Projects database. Some interesting examples are also depicted in Figure 01.
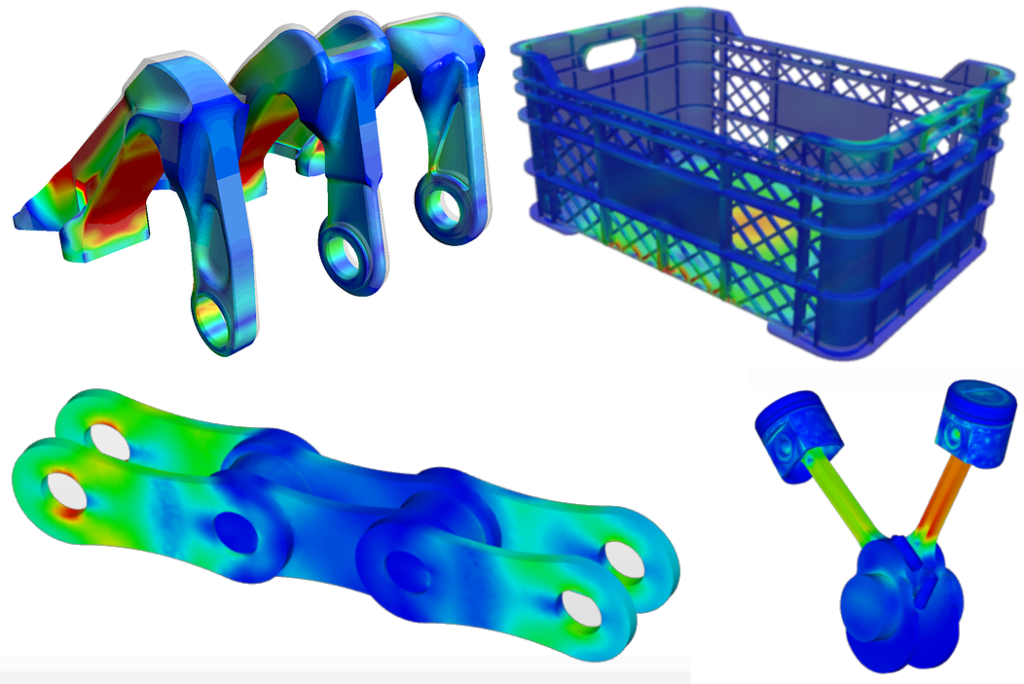
Implicit vs Explicit FEM Implicit vs. Explicit Problems
All of these implicit vs explicit problems are expressed through mathematical partial differential equations (PDEs). While today’s computers can’t single-handedly solve PDEs, they are equipped to solve matrix equations. These matrix equations can be linear or nonlinear. In most structural problems, the nonlinear equations fall into 3 categories:
- Material Nonlinearity: Where deformations and strains are large (i.e., polymer materials)
- Geometric Nonlinearity: Where strains are small, but rotations are large (i.e., thin structures)
- Boundary Nonlinearity: Due to non-linearity of boundary conditions, (i.e., contact problems)
In linear problems, the PDEs reduce to a matrix equation as:
[K]{x} = {f}
and for non-linear static problems as:
[K(x)]{x} = {f}
For dynamic problems, the matrix equations come down to:
[M]{x´´} + [C]{x´} + [K]{x} = {f}
where (.‘) represents the derivative.
Implicit vs Explicit FEM Implicit FEM Analysis
One method of solving for the unknowns {x} is through matrix inversion (or equivalent processes). This is known as an implicit analysis. When the problem is nonlinear, the solution is obtained in a number of steps and the solution for the current step is based on the solution from the previous step. For large models, inverting the matrix is highly expensive and will require advanced iterative solvers (over standard direct solvers). Sometimes, this is also known as the backward Euler integration scheme. These solutions are unconditionally stable and facilitate larger time steps. Despite this advantage, the implicit methods can be extremely time-consuming when solving dynamic and nonlinear problems.
Implicit vs Explicit FEM Explicit FEM Analysis
Explicit analyses aim to solve for acceleration (or otherwise {x´´}). In most cases, the mass matrix is considered as “lumped” and thus a diagonal matrix. Inversion of a diagonal matrix is straightforward and includes inversion of the terms on the diagonal only. Once the accelerations are calculated at the nth step, the velocity at n+1/2 step and displacement at n+1 step are calculated accordingly. In these calculations, the scheme is not unconditionally stable and thus smaller time steps are required. To be more precise, the time step in an explicit finite element analysis must be less than the Courant time step (i.e., the time taken by a sound wave to travel across an element) while implicit analyses have no such limitations.
FEM Differences What is the Difference between Implicit and Explicit FEM?
Explicit FEM is used to calculate the state of a given system at a different time from the current time. In contrast, an implicit analysis finds a solution by solving an equation that includes both the current and later states of the given system. This method requires additional computation and can be harder to implement. However, it will be used in lieu of explicit methodologies when problems are still and using alternative analysis methods is impractical.
For more information, this Wikipedia page provides great examples with illustrations of how both methodologies give numerical approximations to solutions of time-dependent and PDE equations.
FEM Uses When to Use Explicit FEM?
Explicit analysis offers a faster solution in events where there is a dynamic equilibrium or otherwise:
Sum of all forces = mass x acceleration
The explicit method should be used when the strain rates/velocity is over 10 units/second or 10 m/s respectively. These events can be best exampled by extreme scenarios such as an automotive crash, ballistic event, or even meteor impact. In these cases, the material models do not only need to account for the variation of stress with strain but also the strain rate. On this scale, the strain rates play a particularly important contribution.
FEM Uses When to Use Implicit FEM?
The implicit method should be used when the events are much slower and the effects of strain rates are minimal. Once the growth of stress as a function of strain can be established, these can be analyzed using implicit methods. In this case, one can consider a static equilibrium such that:
Sum of all forces = 0
This covers many of the most common engineering problems.
FEM with SImScale Using Parallel Servers for Solutions
The decision to use implicit and explicit FEM directly impacts the speed and potential parallelization. Implicit systems involve matrix inversions that are extremely complicated and do not directly scale with the number of processors. There are several parallel solvers available.
During the solution process, these processors need to continuously communicate with each other. As the number of required processors increases, a point is reached where there is no further advantage of using implicit analysis because the processors stop being time-efficient. As an analogy to illustrate this point, if you delegate a task to 5 people it is much more efficient than if you delegate a task to 100 people in terms of communication and efficiency.
Alternatively, most often explicit problems use a lumped mass matrix that results in de-coupling of equations. Imagine having a diagonal matrix to solve for, where each equation is independent and can be sent to a separate processor. Such problems scale easily with processing power, and can be computed rapidly.
Explore FEA in SimScale
Implicit and Explicit FEM Conclusion
Finite element analysis of an aircraft engine bearing bracket with SimScale
The most important thing to remember when choosing implicit or explicit FEM analysis is to not lose sight of the physics of the problem. Implicit vs. explicit FEM directly influence the physics observed during the simulation, and hence affects the accuracy of the solution process.