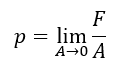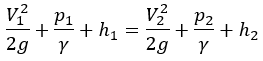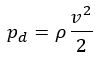Fluid Dynamics: What is Static Pressure?

To better understand what static pressure is, we first need some background and clarification on other terms. The term “pressure” is widely used for many applications within fluid dynamics and thermodynamics, ranging from aerodynamics to plant design. However, we must infer from the context if one is talking about static, total or dynamic pressure.

Most of the definitions mentioned here were taken from the book Mechanics of Fluids by Merle C. Potter, David C. Wiggert, and Bassem H. Ramadan.

Pressure Considerations Important Considerations Before Starting a Computational Wind Engineering Simulation

In fluid mechanics, pressure is defined as a normal force acting on an area. Mathematically, the pressure p on a point is defined as:

The metric units used to measure the pressure are newtons per square meters (N/m²) or, more usually, kilopascal (kPa). The atmospheric pressure at sea level, for example, is 101.3 kPa. The English units for pressure are pounds per square inch (psi) or pounds by square foot (psf).

Air Pressure Simulation Absolute Pressure

Just like temperature, pressure can be measured by different scales, and there are absolute scales for both properties as well. In an ideal vacuum, the absolute pressure reaches zero. This way, there are no molecules in the space to exert pressure. Therefore, it is impossible to achieve negative absolute pressure.

Things become much more complicated when we consider relative measurements of pressure. There is a lot of confusion when it comes to the terminology. It is also common for different software programs to recommend the interpretation of their measurements of pressure in contrasting ways. We’ll talk about how that works with SimScale in a bit.

Air Pressure Simulation Relative Pressures

There are many different relative pressure measurements. The first and most common example is called gauge pressure, which is achieved when measuring pressures relative to the atmospheric pressure. It is also commonly called barometric pressure. It follows then that a conversion from gauge pressure to absolute pressure is obtained by adding it to the atmospheric pressure.

Let’s now examine other pressure measurements that are used within the field of fluid mechanics.

Air Pressure Simulation Static Pressure

To illustrate what total pressure is, let’s begin by checking the famous Bernoulli’s equation:

which measures the difference in velocity and pressure between two points in a flow.

The pressure p in this equation is the static pressure. When measured relative to the atmospheric pressure, the static pressure is the same as the gauge pressure. However, it is possible to measure the static pressure with a vacuum as the reference, so that the value measured equals the absolute pressure.

The static pressure is measured when the fluid is at rest relative to the measurement. It can be measured by a piezometer attached to the wall of the pipe where the fluid is flowing.

Air Pressure Simulation Dynamic Pressure

Notice that when measuring the static pressure before, we don’t consider the velocity effects. If we don’t neglect these effects, there will be an increase in the pressure measured. This increase is called the dynamic pressure. The dynamic pressure is a function of the fluid velocity and density:

Air Pressure Simulation Total Pressure

The total pressure, also called stagnation pressure, is measured by adding the static pressure to the dynamic pressure:

The total pressure is commonly measured with a device called pitot tube. You can see pitot tubes on airplanes, for example, as small holes or metallic tubes hanging in the wings, as shown below:

The velocity inside the pitot tube is zero, making it a stagnation point. Another device, called a pitot-static tube, can be used to measure the dynamic pressure directly. It basically consists of a pitot tube with a static pressure opening.

For most everyday cases, the total pressure is very close to the static pressure. This happens because most systems are designed to ensure low fluid velocities, generally to avoid head loss due to friction, which is proportional to the fluid kinetic energy. In these cases, the distinction between total pressure and static pressure might not be relevant.

Static Pressure Pressure in SimScale

Basically, when simulating fluid flows, we are using the Navier-Stokes equations. Now, when we derive the Navier-Stokes equations for incompressible fluids, the pressure term has only mathematical meaning. Only the pressure gradient, which is responsible for driving the fluid, has physical meaning. In other words, the pressure measurements are used mostly for the solution’s sanity verification.

Following this logic, if we changed the fixed pressure boundary conditions of our simulation by summing a constant value, for example, the resulting flow would not be changed because the pressure gradient would still be the same.

More specifically, for incompressible flows, SimScale uses the specific pressure, which is defined by normalizing the pressure by the density.

SimScale also allows for a rich set of boundary conditions. For more information on setting and using boundary conditions on the SimScale cloud-based simulation platform, you can refer to this page of the documentation. For pressure inlet boundary conditions, the total pressure is used, whereas for pressure outlets, the static or gauge pressure is used. If you’d like to learn more about the SimScale cloud-based platform and its capabilities, download this features overview.

To learn more about air pressure simulation, check out this blog. 

---

---