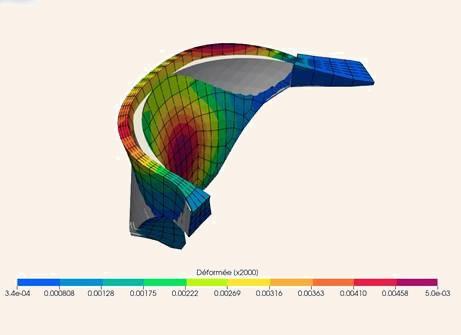
Structural optimization is a design method that ensures designs are strong, efficient, and cost-effective early in their design cycle. Structures must be optimized for the best possible performance with the least material usage, reducing costs and environmental impact.
In industries like aerospace, automotive, and civil engineering, optimizing structures ensures safety, reliability, and sustainability. Yet, traditional methods of structural optimization can be time-consuming and resource-intensive. With cloud-native simulation, engineers can perform complex simulations more quickly and accurately than ever before, enabling a highly efficient and scalable simulation-driven design.
In this article, we will explain why structural optimization is important and how cloud-native solutions like SimScale help achieve that.
What is Structural Optimization?
Structural optimization is the process of designing structures to perform their intended functions most efficiently. It involves creating structures that sustain loads with minimal material use while maintaining strength and durability [1].
The goal is to achieve objectives such as:
- Minimum weight
- Maximum stiffness
- Resistance to instability
This must be done while adhering to constraints like stress limits, displacement restrictions, and geometric boundaries. This involves several key elements and mathematical formulations.
Objective Function (\(f\)): Evaluates design quality, typically minimizing weight, displacement, stress, or cost.
Design Variable (\(x\)): Represents the design, such as geometry or material choice, and can be adjusted during optimization.
State Variable (\(y\)): Indicates the structure’s response, including displacement, stress, strain, or force.
Considering problems that have multiple-objective functions, this leads to a vector optimization problem:
minimize (\(f_1(x,y),f_2(x,y),…,f_l(x,y)\))
Achieving Pareto optimality involves using a weighted sum:
$$ \sum_{i=1}^l w_i f_i(x,y) $$
Where \(w_i ≥ 0\) and \(\sum_{i=1}^l w_i = 1\)
In structural optimization, constraints are crucial in defining the limits within which the structure must perform. These constraints ensure the design meets necessary safety, performance, and practical requirements.
- Behavioral Constraints: On \(y\) written as \(g(y)≤0\)
- Design Constraints: On \(x\), written similarly
- Equilibrium Constraint: the equilibrium constraint is:
$$ K(x)u=F(x) $$
Where:
- \(K(x)\) is the stiffness matrix, dependent on the design.
- \(u\) is the displacement vector.
- \(F(x)\) is the force vector, also design-dependent.
In continuous problems, this often translates to partial differential equations. When addressing nested structural optimization issues by creating a series of explicit first-order approximations, it is necessary to distinguish the objective function and constraint functions in relation to the design variables. This process is referred to as sensitivity analysis. Sensitivity analysis involves finding the derivatives (or sensitivities) of \(f\) and \(g\) with respect to \(x\) to understand how changes in design variables affect the objective and constraints.
Types of Structural Optimization
Here are some major types of structural optimization:
- Sizing Optimization: Sizing optimization involves adjusting the dimensions of structural elements, such as the thickness of beams or the cross-sectional area of columns, to achieve the desired performance.
- Shape Optimization: Shape optimization aims to improve the external contours of a structure to enhance its performance. This process involves modifying the shape of the structure to reduce stress concentrations, improve aerodynamics, or enhance aesthetic appeal.
- Free-Shape Optimization: Free-shape optimization allows for the modification of both the internal and external boundaries of a structure without predefined constraints. This approach provides maximum flexibility in achieving the optimal shape and material distribution.
- Topology Optimization: Topology optimization focuses on finding the best material distribution within a given design space. By determining the optimal layout of the material, engineers can create structures that are lightweight yet strong.
Why is Structural Optimization Important?
Efficiency and Performance
Structural optimization is crucial for improving efficiency and performance in engineering projects. It minimizes weight and material usage, which directly reduces costs.
Additionally, it enhances structural performance by increasing stiffness and stability. This leads to more reliable and cost-effective designs.
Sustainability
Structural optimization contributes to more sustainable engineering practices by optimizing material use and reducing waste. It makes manufacturing processes more eco-friendly by lowering the environmental impact and promoting resource efficiency.
Innovation
Structural optimization, especially through cloud-native simulation, enables the creation of complex and efficient designs that would be unattainable with traditional methods.
Role of Engineering Simulation in Structural Optimization
Engineering simulation plays a pivotal role in structural optimization by providing accurate, predictive models that help engineers test and refine their designs before building physical prototypes. Finite Element Analysis (FEA) allows for the analysis of complex structures under various conditions, ensuring that the final design is both efficient and robust.
Engineers use simulation because it offers significant advantages over traditional methods. Unlike manual calculations and empirical testing, simulation can handle intricate designs and diverse scenarios with precision and speed.
Furthermore, simulation enables engineers to explore multiple design iterations quickly. Traditional methods often involve lengthy trial-and-error processes, while simulation streamlines these steps by providing immediate feedback on design changes.
Advancements with SimScale Cloud-Native Simulation
SimScale is a cloud-native simulation platform that integrates a complete engineering simulation workflow directly into your web browser. It makes advanced structural analysis both technically and economically feasible for any organization.
SimScale is user-friendly, requires no special hardware, offers limitless scalability, and is cost-effective for both individual users and large organizations. Additionally, it provides best-in-class real-time support and collaboration.
SimScale integrates seamlessly with Code_Aster for structural analysis. Code_Aster is a state-of-the-art and intensively validated open-source FEA solver developed by EDF in France. It allows companies to perform advanced FEA simulations efficiently, leveraging cloud computing power to handle the demanding nature of these tasks.
SimScale Applications for Structural Optimization
SimScale offers powerful tools for structural optimization to analyze and refine engineering designs efficiently. Here are some notable examples of structural optimization in SimScale.
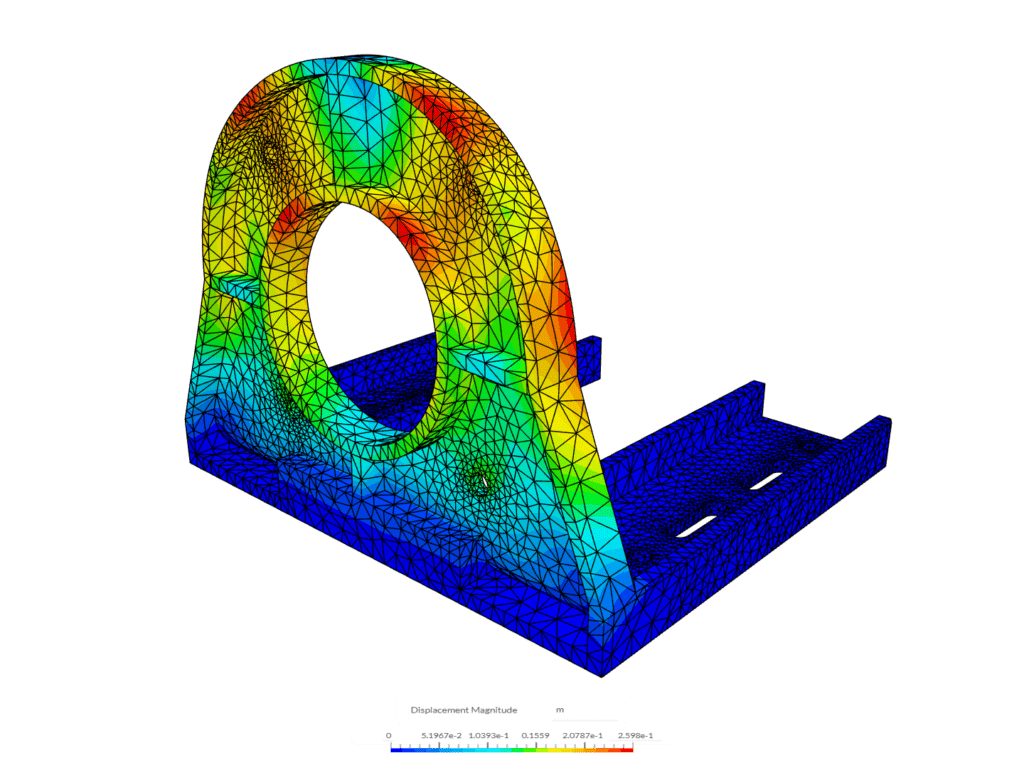
1. Vibration Analysis Of an Electric Motor Bracket
Let’s talk about an example of vibration analysis of an electric motor bracket. In this case, six different bracket designs were evaluated to determine their eigenfrequencies and structural performance. The goal was to identify the optimal design that minimized vibration and maximized stability.
Using SimScale, engineers conducted simultaneous simulations of all six designs, allowing for a comprehensive comparison in a fraction of the time it would take using traditional methods.
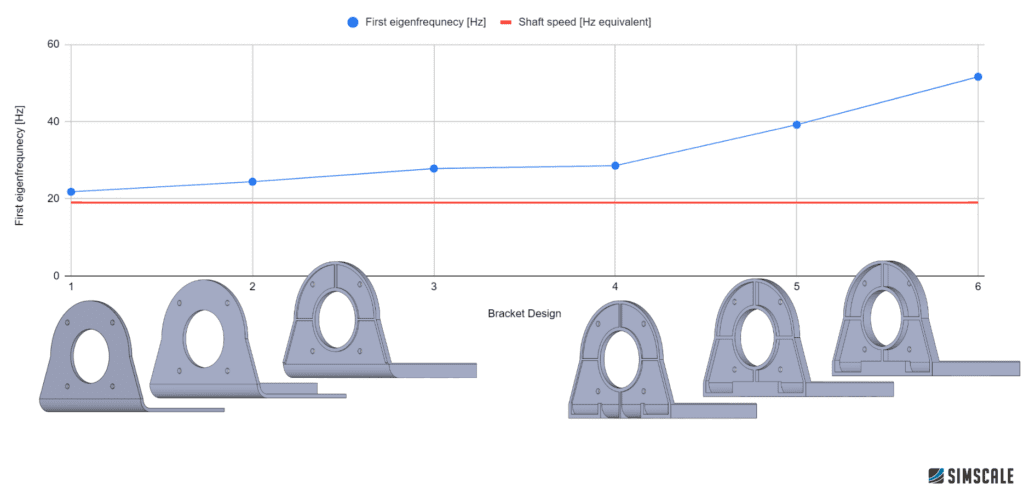
The platform’s cloud-native capabilities meant that extensive computational resources were available on demand. Each design’s first eigenfrequency was plotted against the shaft speed, revealing which configurations were most effective at mitigating vibration issues.
2. Globe Valve Shape Optimization through SimScale
Using tools like SimScale and CAESES®, Gemü’s engineering team employed simulation and optimization to enhance valve performance across various industries. The workflow involved importing CAD geometry into SimScale, running flow simulations with a 1 bar pressure drop, and utilizing CAESES for design experiments.
The focus of the study was the optimization of the GEMÜ 534 globe valve, which is commonly used in industries such as water treatment, chemical processing, and power plants. Traditional CAD tools often struggle with complex geometries and optimization, making CAESES essential for handling sensitive geometric relationships.

The workflow includes parameterizing the CAD model, defining simulation conditions, and running CFD simulations on various design variants. Initial optimization led to an increase in the Kv value from 54.93 to 58.49, with further refinements achieving an 8.3% improvement.
Ready to optimize your designs with SimScale’s powerful tools? Start simulating by clicking below or request a demo and see how SimScale can enhance your engineering projects with precision and efficiency.
References
- Christensen, P.W. & Klarbring, A. (2009) An Introduction to Structural Optimization. Springer Dordrecht. DOI: 10.1007/978-1-4020-8666-3